Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Weinstein, M. I.
and
Xin, J.
1996.
Dynamic stability of vortex solutions of Ginzburg-Landau and nonlinear Schrödinger equations.
Communications in Mathematical Physics,
Vol. 180,
Issue. 2,
p.
389.
Gustafson, S.
1998.
Spectral and Scattering Theory.
p.
33.
Jerrard, Robert L.
and
Soner, Halil Mete
1999.
Scaling limits and regularity results for a class of Ginzburg–Landau systems.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 16,
Issue. 4,
p.
423.
Lin, Fang Hua
1999.
Vortex dynamics for the nonlinear wave equation.
Communications on Pure and Applied Mathematics,
Vol. 52,
Issue. 6,
p.
737.
Bethuel, F.
and
Orlandi, G.
2002.
Uniform estimates for the parabolic Ginzburg–Landau equation.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 8,
Issue. ,
p.
219.
Bethuel, F.
Orlandi, G.
and
Smets, D.
2005.
Collisions and phase-vortex interactions in dissipative Ginzburg-Landau dynamics.
Duke Mathematical Journal,
Vol. 130,
Issue. 3,
Zhang, Yanzhi
Bao, Weizhu
and
Du, Qiang
2007.
The Dynamics and Interaction of Quantized Vortices in the Ginzburg–Landau–Schrödinger Equation.
SIAM Journal on Applied Mathematics,
Vol. 67,
Issue. 6,
p.
1740.
Bethuel, F.
Orlandi, G.
and
Smets, D.
2007.
Dynamics of Multiple Degree Ginzburg-Landau Vortices.
Communications in Mathematical Physics,
Vol. 272,
Issue. 1,
p.
229.
Bethuel, F.
Orlandi, G.
and
Smets, D.
2008.
Vortex motion and phase-vortex interaction in dissipative Ginzburg-Landau dynamics.
Journées équations aux dérivées partielles,
p.
1.
Tice, Ian
2010.
Ginzburg‐Landau vortex dynamics driven by an applied boundary current.
Communications on Pure and Applied Mathematics,
Vol. 63,
Issue. 12,
p.
1622.
Bao, Weizhu
and
Tang, Qinglin
2013.
Numerical Study of Quantized Vortex Interaction in the Ginzburg-Landau Equation on Bounded Domains.
Communications in Computational Physics,
Vol. 14,
Issue. 3,
p.
819.
Chen, Ko-Shin
and
Sternberg, Peter
2014.
Dynamics of Ginzburg-Landau and Gross-Pitaevskii vortices on manifolds.
Discrete & Continuous Dynamical Systems - A,
Vol. 34,
Issue. 5,
p.
1905.
García-Cervera, Carlos J.
Giorgi, Tiziana
and
Joo, Sookyung
2020.
Boundary Vortex Formation in Polarization-Modulated Orthogonal Smectic Liquid Crystals.
SIAM Journal on Applied Mathematics,
Vol. 80,
Issue. 5,
p.
2024.


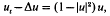
 . Let
. Let