Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wei, Juncheng
Winter, Matthias
and
Yang, Wen
2017.
Stable spike clusters for the precursor Gierer–Meinhardt system in $$\mathbb {R}^2$$ R 2.
Calculus of Variations and Partial Differential Equations,
Vol. 56,
Issue. 5,
Kolokolnikov, Theodore
and
Wei, Juncheng
2018.
Pattern Formation in a Reaction-Diffusion System with Space-Dependent Feed Rate.
SIAM Review,
Vol. 60,
Issue. 3,
p.
626.
Krause, Andrew L.
Klika, Václav
Woolley, Thomas E.
and
Gaffney, Eamonn A.
2018.
Heterogeneity induces spatiotemporal oscillations in reaction-diffusion systems.
Physical Review E,
Vol. 97,
Issue. 5,
Wei, Juncheng
and
Yang, Wen
2019.
Multi-bump Ground States of the Fractional Gierer–Meinhardt System on the Real Line.
Journal of Dynamics and Differential Equations,
Vol. 31,
Issue. 1,
p.
385.
Ao, Weiwei
Wei, Juncheng
and
Winter, Matthias
2019.
Stable boundary spike clusters for the two-dimensional Gierer–Meinhardt system.
Journal de Mathématiques Pures et Appliquées,
Vol. 121,
Issue. ,
p.
1.
Ao, Weiwei
Wei, Juncheng
and
Winter, Matthias
2020.
Stable spike clusters on a compact two-dimensional Riemannian manifold.
Journal of Differential Equations,
Vol. 268,
Issue. 7,
p.
3665.
Bastiaansen, Robbin
Chirilus-Bruckner, Martina
and
Doelman, Arjen
2020.
Pulse Solutions for an Extended Klausmeier Model with Spatially Varying Coefficients.
SIAM Journal on Applied Dynamical Systems,
Vol. 19,
Issue. 1,
p.
1.
Kolokolnikov, Theodore
and
Xie, Shuangquan
2020.
Spike density distribution for the Gierer–Meinhardt model with precursor.
Physica D: Nonlinear Phenomena,
Vol. 402,
Issue. ,
p.
132247.
Kolokolnikov, Theodore
Paquin-Lefebvre, Frédéric
and
Ward, Michael J
2020.
Stable asymmetric spike equilibria for the Gierer–Meinhardt model with a precursor field.
IMA Journal of Applied Mathematics,
Vol. 85,
Issue. 4,
p.
605.
Wong, Tony
and
Ward, Michael J.
2021.
Spot patterns in the 2‐D Schnakenberg model with localized heterogeneities.
Studies in Applied Mathematics,
Vol. 146,
Issue. 4,
p.
779.
Ishii, Yuta
2021.
Concentration phenomena on Y-shaped metric graph for the Gierer–Meinhardt model with heterogeneity.
Nonlinear Analysis,
Vol. 205,
Issue. ,
p.
112220.
Ishii, Yuta
2021.
The effect of heterogeneity on one-peak stationary solutions to the Schnakenberg model.
Journal of Differential Equations,
Vol. 285,
Issue. ,
p.
321.
Yang, Rui
and
Yu, Xiao-Qing
2022.
Turing–Hopf Bifurcation in Diffusive Gierer–Meinhardt Model.
International Journal of Bifurcation and Chaos,
Vol. 32,
Issue. 04,
Ishii, Yuta
2022.
Stability Analysis of Spike Solutions to the Schnakenberg Model with Heterogeneity on Metric Graphs.
Journal of Nonlinear Science,
Vol. 32,
Issue. 1,
Praditia, Timothy
Karlbauer, Matthias
Otte, Sebastian
Oladyshkin, Sergey
Butz, Martin V.
and
Nowak, Wolfgang
2022.
Learning Groundwater Contaminant Diffusion‐Sorption Processes With a Finite Volume Neural Network.
Water Resources Research,
Vol. 58,
Issue. 12,
de Medeiros, Markus
Wei, Jun-Cheng
and
Yang, Wen
2022.
Existence and stability of symmetric and asymmetric patterns for the half-Laplacian Gierer–Meinhardt system in one-dimensional domain.
Mathematical Models and Methods in Applied Sciences,
Vol. 32,
Issue. 06,
p.
1193.
Ishii, Yuta
2023.
Multi-peak solutions for the Schnakenberg model with heterogeneity on star shaped graphs.
Physica D: Nonlinear Phenomena,
Vol. 446,
Issue. ,
p.
133679.
Hu, Yeyao
and
Xie, Weihong
2023.
Cluster solutions for the FitzHugh-Nagumo system with Neumann boundary conditions.
Journal of Differential Equations,
Vol. 374,
Issue. ,
p.
95.
Wang, Bingqi
and
Zhou, Xiangyu
2024.
Single peak solutions for an elliptic system of FitzHugh–Nagumo type.
Journal of Fixed Point Theory and Applications,
Vol. 26,
Issue. 2,
Chen, Yuanxian
Li, Ji
Shen, Jianhe
and
Zhang, Qian
2024.
Pattern formations in nonlinear reaction-diffusion systems with strong localized impurities.
Journal of Differential Equations,
Vol. 402,
Issue. ,
p.
250.
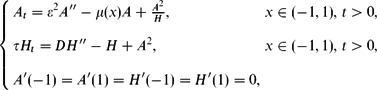 $$\begin{equation*}
\left\{
\begin{array}{ll}
A_t=\epsilon^2 A''- \mu(x) A+\frac{A^2}{H}, &x\in(-1, 1),\,t>0,\\[3mm]
\tau H_t=D H'' -H+ A^2, & x\in (-1, 1),\,t>0,\\[3mm]
A' (-1)= A' (1)= H' (-1) = H' (1) =0,
\end{array}
\right.
\end{equation*}$$
$$\begin{equation*}
\left\{
\begin{array}{ll}
A_t=\epsilon^2 A''- \mu(x) A+\frac{A^2}{H}, &x\in(-1, 1),\,t>0,\\[3mm]
\tau H_t=D H'' -H+ A^2, & x\in (-1, 1),\,t>0,\\[3mm]
A' (-1)= A' (1)= H' (-1) = H' (1) =0,
\end{array}
\right.
\end{equation*}$$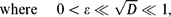 $$\begin{equation*}\mbox{where } \quad 0<\epsilon \ll\sqrt{D}\ll 1, \quad
\end{equation*}$$
$$\begin{equation*}\mbox{where } \quad 0<\epsilon \ll\sqrt{D}\ll 1, \quad
\end{equation*}$$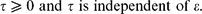 $$\begin{equation*}
\tau\geq 0
\mbox{ and
$\tau$ is independent of $\epsilon$.
}
\end{equation*}$$
$$\begin{equation*}
\tau\geq 0
\mbox{ and
$\tau$ is independent of $\epsilon$.
}
\end{equation*}$$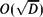 $O(\sqrt{D})$ scale of the inhibitor diffusivity and the O(ε) scale of the activator diffusivity; (iii) the expressions can be made explicit and often have a particularly simple form.
$O(\sqrt{D})$ scale of the inhibitor diffusivity and the O(ε) scale of the activator diffusivity; (iii) the expressions can be made explicit and often have a particularly simple form.