Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-05T01:03:10.112Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of weakly dissipative Reissner–Mindlin–Timoshenko plates: A sharp result

Published online by Cambridge University Press:  27 April 2017

A. D. S. CAMPELO ,
D. S. ALMEIDA JÚNIOR  and
M. L. SANTOS
A. D. S. CAMPELO
Affiliation:
Department of Mathematics – Federal University of Pará, Augusto Corrêa Street, 01, 66075-110, Belém, Pará, Brazil emails: [email protected], [email protected], [email protected]
D. S. ALMEIDA JÚNIOR
Affiliation:
Department of Mathematics – Federal University of Pará, Augusto Corrêa Street, 01, 66075-110, Belém, Pará, Brazil emails: [email protected], [email protected], [email protected]
M. L. SANTOS
Affiliation:
Department of Mathematics – Federal University of Pará, Augusto Corrêa Street, 01, 66075-110, Belém, Pará, Brazil emails: [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present article, we show that there exists a critical number that stabilizes the Reissner–Mindlin–Timoshenko system with frictional dissipation acting on rotation angles. We identify two speed characteristics v12:=K/ρ1 and v22:=D/ρ2, and we show that the system is exponentially stable if and only if

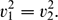\begin{equation*} v_{1}^{2}=v_{2}^{2}. \end{equation*}
For v12 ≠ v22, we prove that the system is polynomially stable and determine an optimal estimate for the decay. To confirm our analytical results, we compute the numerical solutions by means of several numerical experiments by using a finite difference method.

Keywords

Reissner-Mindlin-Timoshenko systemwave propagation speedexponential stabilityoptimal decayfinite difference
Type
Papers
Information
European Journal of Applied Mathematics , Volume 29 , Issue 2 , April 2018 , pp. 226 - 252
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Almeida Júnior, D. S., Santos, M. L. & Muñoz Rivera, J. E. (2013) Stability to weakly dissipative Timoshenko systems. Math. Methods Appl. Sci. 36 (14), 1965–1976.Google Scholar
[2] Almeida Júnior, D. S. & Muñoz Rivera, J. E. (2015) Stability criterion to explicit finite difference applied to the Bresse system. Afrika Mathematika 26 (5), 761–778.CrossRefGoogle Scholar
[3] Ammar-Khodja, F., Benabdallah, A., Muñoz Rivera, J. E. & Racke, R. (2003) Energy decay for Timoshenko systems of memory type. J. Differ Equ. 194 (1), 82–115.Google Scholar
[4] Anguelov, R., Djoko, J. K. & Lubuma, J. M.-S. (2008) Energy properties preserving schemes for Burgers' equation. Numer. Methods Partial Differ. Equ. 24 (1), 41–59.Google Scholar
[5] Alves, M., Muñoz Rivera, J. E., Sepúlveda, M., Villagrán, O. V. & Zegarra Garay, M. (2014) The asymptotic behavior of the linear transmission problem in viscoelasticity. Math. Nachr. 287 (5–6), 483–497.Google Scholar
[6] Borichev, A. & Tomilov, Y. (2009) Optimal polynomial decay of functions and operator semigroups. Math. Ann. 347 (2), 455–478.Google Scholar
[7] Brezis, H. (1992) Analyse Fonctionelle, Théorie et Applications Masson, Paris.Google Scholar
[8] Campelo, A., Almeida Júnior, D. & Santos, M. L. (2016) Stability to the dissipative Reissner-Mindlin-Timoshenko acting on displacement equation. Eur. J. Appl. Math. 27 (2), 157–193.Google Scholar
[9] Fernándes Sare, H. D. (2009) On the stability of Mindlin–Timoshenko plates. Q. Appl Math LXVII (2), 249–263.CrossRefGoogle Scholar
[10] Grobbelaar-Van Dalsen, M. (2011) Strong stabilization of models incorporating the thermoelastic Reissner–Mindlin plate equations with second sound. Appl. Anal. 90 (9), 1419–1449.Google Scholar
[11] Grobbelaar-Van Dalsen, M. (2013) Stabilization of a thermoelastic Mindlin-Timoshenko plate model revisited, Z. Angew. Math. Phys. 64 (4), 1305–1325.Google Scholar
[12] Grobbelaar-Van Dalsen, M. (2015) Polynomial decay rate of a thermoelastic Mindlin–Timoshenko plate model with Dirichlet boundary conditions. Z. Angew. Math. Phys. 66 (1), 113–128.Google Scholar
[13] Haraux, A. (1989) Une remarque sur la stabilisation de certains systèmes du deuxième ordere en tems. Port. Math. 46 (3), 245–258.Google Scholar
[14] Huang, F. (1985) Characteristic conditions for exponential stability of linear dynamical systems in Hilbert spaces. Ann. Differential Equations, 1 (1), 43–56.Google Scholar
[15] Jovanović, B. S. & Süli, E. (2014) Analysis of Finite Difference Schemes. For Linear Partial Differential Equations with Generalized Solutions. Springer Series in Computational Mathematics, Vol. 46, Springer London, 408 pages.CrossRefGoogle Scholar
[16] Kim, J. & Renardy, Y. (1987) Boundary control of the Timoshenko beam. SIAM J. Control Optim. 25 (6), 1417–1429.CrossRefGoogle Scholar
[17] Lagnese, J. & Lions, J. (1988) Modelling, Analysis and Control of Thin Plates. Collection RMA, Masson, Paris.Google Scholar
[18] Lagnese, J. (1989) Boundary Stabilization of Thin Plates. SIAM, Philadelphia.Google Scholar
[19] Liu, Z. & Zheng, S. (1999) Semigroups Associated with Dissipative Systems, In CRC Reseach Notes in Mathematics, Vol. 398, Chapman & Hall, CRC Press. Taylor & Francis Group.Google Scholar
[20] Muñoz Rivera, J. E. & Portillo Oquendo, H. (2003) Asymptotic behavior on a Mindlin–Timoshenko plate with viscoelastic dissipation on the boundary. Funkcialaj Ekvacioj. 46 (3), 363–382.CrossRefGoogle Scholar
[21] Muñoz Rivera, J. E. & Racke, R. (2002) Mildly dissipative nonlinear Timoshenko systems–Global existence and exponential stability. J. Math. Anal. Appl. 276 (1), 248–278.CrossRefGoogle Scholar
[22] Muñoz Rivera, J. & Racke, R. (2003) Global stability for damped Timoshenko systems. Discrete Continuous Dyn. Syst. 9 (6), 1625–1639.Google Scholar
[23] Negreanu, M. & Zuazua, E. (2003) Uniform boundary controllability of a discrete 1-D wave equations. Syst. Control Lett. 48 (3–4), 261–279.Google Scholar
[24] Pazy, A. (1983) Semigroups of Linear Operators and Applications to Partial Differential Equations. Vol. 44, Springer-Verlag, New York, 282 pages.Google Scholar
[25] Pokojovy, M. (2015) On stability of hyperbolic thermoelastic Reissner-Mindlin-Timoshenko plates. Math. Methods Appl. Sci. 38 (7), 1225–1246.Google Scholar
[26] Prüss, J. (1984) On the spectrum of C 0-semigroups. Trans. Am. Math. Soc. 284, 847–857.Google Scholar
[27] Raposo, C., Ferreira, J., Santos, M. L. & Castro, N. (2005) Exponential stability for the Timoshenko beam with two weak dampings. Appl. Math. Lett. 18 (5), 535–541.Google Scholar
[28] Santos, M. (2002) Decay rates for solutions of a Timoshenko system with a memory condition at the boundary. Abstr. Appl. Anal. 7 (10), 531–546.CrossRefGoogle Scholar
[29] Santos, M., Almeida Júnior, D. S. & Muñoz Rivera, J. (2012) The stability number of the Timoshenko system with second sound. J. Differ. Equ. 253 (9), 2715–2733.Google Scholar
[30] Soufyane, A. (1999) Stabilisation de la poutre de Timoshenko. C. R. Acad. Sci., Paris, Série I - Math. 328 (8), 731–734.Google Scholar
[31] Süli, E. & Mayers, D. (2003) An Introduction to Numerical Analysis. Cambridge University Press, 433 pages.CrossRefGoogle Scholar
[32] Wright, J. (1987) A mixed time integration method for Timoshenko and Mindlin type elements. Commun. Appl. Numer. Methods 3 (3), 181–185.Google Scholar
[33] Wright, J. (1998) Numerical stability of a variable time step explicit method for Timoshenko and Mindlin type structures. Commun. Numer. Methods Eng. 14 (2), 81–86.Google Scholar