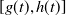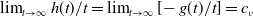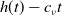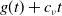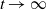1. Introduction
The West Nile virus (WNv) is an arthropod-borne flavivirus that causes epidemics of febrile illness and sporadic encephalitis in many parts of the world. The incidence mechanism involves primarily interacting bird and mosquito populations, with birds acting as hosts and mosquitoes as vectors of the virus. For the prediction and prevention of the spreading of WNv, it is important to understand its temporal and spatial spreading dynamics.
Mathematical models may help us to understand the spreading process and to formulate suitable strategy to control the spreading of the virus. Ignoring spatial variations of the involved populations, several ODE models have been used to describe the WNv dynamics; see, for instance, Abdelrazec et al. [Reference Abdelrazec, Lenhart and Zhu1], Bowman et al. [Reference Bowman, Gumel, Wu, van den Driessche and Zhu2], Kenkre et al. [Reference Kenkre, Parmenter, Peixoto and Sadasiv22], Wonham et al. [Reference Wonham, De-Camino-Beck and Lewis35] and references therein. The dynamics of such an ODE model is governed by a basic reproduction number
![]() $\mathcal R_0$
. To be more specific, the virus tends to extinction if
$\mathcal R_0$
. To be more specific, the virus tends to extinction if
![]() $\mathcal R_0\lt 1$
and it persists if
$\mathcal R_0\lt 1$
and it persists if
![]() $\mathcal R_0\gt 1$
.
$\mathcal R_0\gt 1$
.
To include the possible impact of spatial movement of WNv, Lewis et al. [Reference Lewis, Renclawowicz and van den Driessche24] first introduced suitable diffusion terms in the ODE model by considering the following reaction–diffusion system:
 \begin{eqnarray} \begin{cases} H_t=D_R H_{xx}+\alpha _R\beta _R\dfrac{N_R-H}{N_R}M-\gamma _RH,& x\in \mathbb{R}, t\gt 0, \\ M_t=D_V M_{xx}+\alpha _V\beta _R\dfrac{A_V-M}{N_R}H-d_V M,& x\in \mathbb{R}, t\gt 0, \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} H_t=D_R H_{xx}+\alpha _R\beta _R\dfrac{N_R-H}{N_R}M-\gamma _RH,& x\in \mathbb{R}, t\gt 0, \\ M_t=D_V M_{xx}+\alpha _V\beta _R\dfrac{A_V-M}{N_R}H-d_V M,& x\in \mathbb{R}, t\gt 0, \end{cases} \end{eqnarray}
where
![]() $H(x,t)$
and
$H(x,t)$
and
![]() $M(x,t)$
denote the densities of the infected bird and mosquito populations at spatial location
$M(x,t)$
denote the densities of the infected bird and mosquito populations at spatial location
![]() $x$
and time
$x$
and time
![]() $t$
, respectively. The parameters here are all positive constants:
$t$
, respectively. The parameters here are all positive constants:
![]() $D_R, D_V$
stand for the diffusion rates of birds and mosquitoes, respectively;
$D_R, D_V$
stand for the diffusion rates of birds and mosquitoes, respectively;
![]() $\alpha _V, \alpha _R$
represent the WNv transmission probability per bite to mosquitoes and to birds, respectively;
$\alpha _V, \alpha _R$
represent the WNv transmission probability per bite to mosquitoes and to birds, respectively;
![]() $\beta _R$
is the biting rate of mosquitoes on birds;
$\beta _R$
is the biting rate of mosquitoes on birds;
![]() $\gamma _R$
is the recovery rate of birds from WNv;
$\gamma _R$
is the recovery rate of birds from WNv;
![]() $d_V$
is the mosquito death rate;
$d_V$
is the mosquito death rate;
![]() $N_R$
is the total number of susceptible and infected birds; and
$N_R$
is the total number of susceptible and infected birds; and
![]() $A_V$
is the total number of susceptible and infected mosquitoes, which are assumed to be constants during the infection process.
$A_V$
is the total number of susceptible and infected mosquitoes, which are assumed to be constants during the infection process.
To simplify the notations, we set
 \begin{equation*} \begin {aligned} &a_1\,:\!=\frac {\alpha _R\beta _R}{N_R},\ a_2\,:\!=\frac {\alpha _V\beta _R}{N_R},\ b_1\,:\!=\gamma _R,\ b_2\,:\!=d_V,\\ &\ \ \ e_1\,:\!=N_R,\ e_2\,:\!=A_V,d_1\,:\!=D_R,\ d_2\,:\!=D_V, \end {aligned} \end{equation*}
\begin{equation*} \begin {aligned} &a_1\,:\!=\frac {\alpha _R\beta _R}{N_R},\ a_2\,:\!=\frac {\alpha _V\beta _R}{N_R},\ b_1\,:\!=\gamma _R,\ b_2\,:\!=d_V,\\ &\ \ \ e_1\,:\!=N_R,\ e_2\,:\!=A_V,d_1\,:\!=D_R,\ d_2\,:\!=D_V, \end {aligned} \end{equation*}
and then system (1.1) is transformed to the following non-dimensional form:
 \begin{eqnarray} \begin{cases} H_t=d_1 H_{xx}+a_1(e_1-H)M-b_1H,&\quad x\in \mathbb{R},\, t\gt 0,\\ M_t=d_2 M_{xx}+a_2(e_2-M)H-b_2 M,&\quad x\in \mathbb{R},\, t\gt 0. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} H_t=d_1 H_{xx}+a_1(e_1-H)M-b_1H,&\quad x\in \mathbb{R},\, t\gt 0,\\ M_t=d_2 M_{xx}+a_2(e_2-M)H-b_2 M,&\quad x\in \mathbb{R},\, t\gt 0. \end{cases} \end{eqnarray}
The basic reproduction number arising from the ODE version of (1.2) is given by:
Clearly,
![]() $\mathcal R_0\gt 1$
is equivalent to
$\mathcal R_0\gt 1$
is equivalent to
![]() $a_1a_2e_1e_2\gt b_1b_2$
. Moreover, system (1.2) admits the trivial equilibrium
$a_1a_2e_1e_2\gt b_1b_2$
. Moreover, system (1.2) admits the trivial equilibrium
![]() $(0, 0)$
, and if
$(0, 0)$
, and if
![]() $a_1a_2e_1e_2\gt b_1b_2$
, then it further has a unique positive constant endemic equilibrium:
$a_1a_2e_1e_2\gt b_1b_2$
, then it further has a unique positive constant endemic equilibrium:
It is proved in [Reference Lewis, Renclawowicz and van den Driessche24] that if
![]() $\mathcal R_0\gt 1$
, (1.2) has a travelling wave solution
$\mathcal R_0\gt 1$
, (1.2) has a travelling wave solution
![]() $(H(x-ct), M(x-ct))$
satisfying
$(H(x-ct), M(x-ct))$
satisfying
for every
![]() $c\geq c^*$
, where
$c\geq c^*$
, where
![]() $c^*\gt 0$
is the minimal value with such a property. Moreover, Theorem 6.2 in [Reference Lewis, Renclawowicz and van den Driessche24] shows that if
$c^*\gt 0$
is the minimal value with such a property. Moreover, Theorem 6.2 in [Reference Lewis, Renclawowicz and van den Driessche24] shows that if
![]() $H(x, 0)$
and
$H(x, 0)$
and
![]() $M(x,0)$
are non-negative with non-empty compact supports, then for all small
$M(x,0)$
are non-negative with non-empty compact supports, then for all small
![]() $\epsilon \gt 0$
,
$\epsilon \gt 0$
,
and
Biologically, this means that the virus spreads with speed
![]() $c^*$
.
$c^*$
.
However, since the strong maximum principle implies that
![]() $H(x, t)\gt 0$
and
$H(x, t)\gt 0$
and
![]() $M(x,t)\gt 0$
for all
$M(x,t)\gt 0$
for all
![]() $x\in \mathbb R$
once
$x\in \mathbb R$
once
![]() $t\gt 0$
, the above mathematical result for (1.2) does not provide a precise location of the spreading front of the epidemic region. When we say the virus spreads with speed
$t\gt 0$
, the above mathematical result for (1.2) does not provide a precise location of the spreading front of the epidemic region. When we say the virus spreads with speed
![]() $c^*$
, it is meant that for any small
$c^*$
, it is meant that for any small
![]() $\delta \gt 0$
, the level sets
$\delta \gt 0$
, the level sets
![]() $\{x\,:\, H(x,t)=\delta \}$
and
$\{x\,:\, H(x,t)=\delta \}$
and
![]() $\{x\,:\, M(x,t)=\delta \}$
move in space with asymptotic speed
$\{x\,:\, M(x,t)=\delta \}$
move in space with asymptotic speed
![]() $c^*$
.
$c^*$
.
To better describe the location of the spreading front of the disease, Lin and Zhu [Reference Lin and Zhu25] use a modified version of (1.2) to model the spreading of WNv, where the spreading front is explicitly expressed in the model as free boundaries. Under our notations here, the model of [Reference Lin and Zhu25] has the form:
 \begin{eqnarray} \begin{cases} H_t=d_1 H_{xx}+a_1(e_1-H)M-b_1H,&g(t)\lt x\lt h(t),\quad t\gt 0,\\ M_t=d_2 M_{xx}+a_2(e_1-M)H-b_2M,&g(t)\lt x\lt h(t),\quad t\gt 0,\\ H(x,t)=M(x,t)=0,&x=g(t) \mbox{ or } x=h(t),\;\; t\gt 0,\\ g(0)=-h_0,\; \quad g^{\prime}(t)=-\nu H_{x}(g(t),t),& t\gt 0,\\ h(0)=h_0,\quad h^{\prime}(t)=-\nu H_{x}(h(t),t),& t\gt 0,\\ H(x,0)=H_{0}(x),\quad M(x,0)=M_{0}(x),&-h_0\leq x\leq h_0. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} H_t=d_1 H_{xx}+a_1(e_1-H)M-b_1H,&g(t)\lt x\lt h(t),\quad t\gt 0,\\ M_t=d_2 M_{xx}+a_2(e_1-M)H-b_2M,&g(t)\lt x\lt h(t),\quad t\gt 0,\\ H(x,t)=M(x,t)=0,&x=g(t) \mbox{ or } x=h(t),\;\; t\gt 0,\\ g(0)=-h_0,\; \quad g^{\prime}(t)=-\nu H_{x}(g(t),t),& t\gt 0,\\ h(0)=h_0,\quad h^{\prime}(t)=-\nu H_{x}(h(t),t),& t\gt 0,\\ H(x,0)=H_{0}(x),\quad M(x,0)=M_{0}(x),&-h_0\leq x\leq h_0. \end{cases} \end{eqnarray}
The functions
![]() $x=g(t)$
and
$x=g(t)$
and
![]() $x=h(t)$
are the moving boundaries to be determined;
$x=h(t)$
are the moving boundaries to be determined;
![]() $\nu$
is a given constant. The initial functions satisfy, for some
$\nu$
is a given constant. The initial functions satisfy, for some
![]() $h_0\gt 0$
,
$h_0\gt 0$
,
 \begin{eqnarray*} \begin{cases} H_0\in C^2((\!-h_0,h_0))\cap C([\!-h_0,h_0]),\ H_0(\!-h_0)=H_0(h_0)=0, \ 0\lt H_0\leq e_1 \mbox{ in }(\!-h_0,h_0),\\ M_0\in C^2((\!-h_0,h_0))\cap C([\!-h_0,h_0]),\ M_0(\!-h_0)=M_0(h_0)=0, \ 0\lt M_0\leq e_2 \mbox{ in }(\!-h_0,h_0). \end{cases} \end{eqnarray*}
\begin{eqnarray*} \begin{cases} H_0\in C^2((\!-h_0,h_0))\cap C([\!-h_0,h_0]),\ H_0(\!-h_0)=H_0(h_0)=0, \ 0\lt H_0\leq e_1 \mbox{ in }(\!-h_0,h_0),\\ M_0\in C^2((\!-h_0,h_0))\cap C([\!-h_0,h_0]),\ M_0(\!-h_0)=M_0(h_0)=0, \ 0\lt M_0\leq e_2 \mbox{ in }(\!-h_0,h_0). \end{cases} \end{eqnarray*}
More explanations of the background and justification of the model (1.3) can be found in Section 2 of [Reference Lin and Zhu25].
In (1.3), the population range of infected birds is represented by the changing interval
![]() $(g(t), h(t))$
, and the virus carrying mosquitoes are assumed to have the same population range. The expanding rate of the range boundaries is assumed to satisfy
$(g(t), h(t))$
, and the virus carrying mosquitoes are assumed to have the same population range. The expanding rate of the range boundaries is assumed to satisfy
![]() $g^{\prime}(t)=-\nu H_{x}(g(t),t)$
and
$g^{\prime}(t)=-\nu H_{x}(g(t),t)$
and
![]() $h^{\prime}(t)=-\nu H_x(h(t),t)$
, which coincides with the well-known Stefan free boundary condition. A detailed deduction of this free boundary condition based on suitable biological assumptions is given in [Reference Bunting, Du and Krakowski3]: if one assumes that the population range increases at a sacrifice of the species near the front, then these free boundary equations are satisfied with
$h^{\prime}(t)=-\nu H_x(h(t),t)$
, which coincides with the well-known Stefan free boundary condition. A detailed deduction of this free boundary condition based on suitable biological assumptions is given in [Reference Bunting, Du and Krakowski3]: if one assumes that the population range increases at a sacrifice of the species near the front, then these free boundary equations are satisfied with
![]() $\nu =d_1/k$
, where
$\nu =d_1/k$
, where
![]() $d_1$
is the diffusion rate of
$d_1$
is the diffusion rate of
![]() $H$
and
$H$
and
![]() $k$
is the number of units of population loss of
$k$
is the number of units of population loss of
![]() $H$
at the free boundary (spreading front) per unit time per unit volume/area. Similar free boundary conditions have also been used for analogous purposes in other models; see [Reference Chen and Friedman4, Reference Du and Lin9, Reference Du, Matsuzawa and Zhou11, Reference Du, Matsuzawa and Zhou12, Reference Du, Wei and Zhou16, Reference Gu, Lou and Zhou18–Reference Kaneko, Matsuzawa and Yamada21, Reference Wang31–Reference Wang, Nie and Du34] for a small sample.
$H$
at the free boundary (spreading front) per unit time per unit volume/area. Similar free boundary conditions have also been used for analogous purposes in other models; see [Reference Chen and Friedman4, Reference Du and Lin9, Reference Du, Matsuzawa and Zhou11, Reference Du, Matsuzawa and Zhou12, Reference Du, Wei and Zhou16, Reference Gu, Lou and Zhou18–Reference Kaneko, Matsuzawa and Yamada21, Reference Wang31–Reference Wang, Nie and Du34] for a small sample.
It was shown in [Reference Lin and Zhu25] that (1.3) has a unique solution
![]() $(H,M,g,h)$
which is defined for all
$(H,M,g,h)$
which is defined for all
![]() $t\gt 0$
, where
$t\gt 0$
, where
![]() $H, M\in C^{2,1}(\overline \Omega )$
and
$H, M\in C^{2,1}(\overline \Omega )$
and
![]() $g, h\in C^1([0,\infty ))$
with
$g, h\in C^1([0,\infty ))$
with
![]() $\Omega \,:\!=\{(x,t)\,:\, x\in (g(t), h(t)),\ t\gt 0\}$
, and when
$\Omega \,:\!=\{(x,t)\,:\, x\in (g(t), h(t)),\ t\gt 0\}$
, and when
![]() $\mathcal R_0\leq 1$
, the virus always vanishes eventually, that is,
$\mathcal R_0\leq 1$
, the virus always vanishes eventually, that is,
If
![]() $\mathcal R_0\gt 1$
, then a spreading–vanishing dichotomy holds true:
$\mathcal R_0\gt 1$
, then a spreading–vanishing dichotomy holds true:
Either (1.4) holds, or the virus spreads successfully, namely,
Criteria for vanishing and spreading are also established in [Reference Lin and Zhu25]. More precisely, there is a critical length
![]() $L^*\gt 0$
so that either the range size
$L^*\gt 0$
so that either the range size
![]() $h(t)-g(t)$
reaches
$h(t)-g(t)$
reaches
![]() $L^*$
at a finite time and then spreading happens, or
$L^*$
at a finite time and then spreading happens, or
![]() $h(t)-g(t)$
stays below this critical length
$h(t)-g(t)$
stays below this critical length
![]() $L^*$
for all time and then vanishing occurs. In particular, if
$L^*$
for all time and then vanishing occurs. In particular, if
![]() $h(0)-g(0)=2h_0\geq L^*$
, then spreading always happens.
$h(0)-g(0)=2h_0\geq L^*$
, then spreading always happens.
To determine the asymptotic spreading speed of the virus modelled by (1.3), we need to consider the following semi-wave problem:
 \begin{eqnarray} \left \{\begin{aligned} &d_1 u^{\prime\prime}-cu^{\prime}+a_1(e_1-u)v-b_1u=0,\quad 0\lt s\lt \infty,\\ &d_2 v^{\prime\prime}-cv^{\prime}+a_2(e_2-v)u-b_2v=0,\quad 0\lt s\lt \infty,\\ &(u(0),v(0))=(0,0),\quad (u(\infty ),v(\infty ))=(H^*, M^*). \end{aligned}\right. \end{eqnarray}
\begin{eqnarray} \left \{\begin{aligned} &d_1 u^{\prime\prime}-cu^{\prime}+a_1(e_1-u)v-b_1u=0,\quad 0\lt s\lt \infty,\\ &d_2 v^{\prime\prime}-cv^{\prime}+a_2(e_2-v)u-b_2v=0,\quad 0\lt s\lt \infty,\\ &(u(0),v(0))=(0,0),\quad (u(\infty ),v(\infty ))=(H^*, M^*). \end{aligned}\right. \end{eqnarray}
Proposition 1.1. (Theorem 3.2 of [Reference Wang, Nie and Du33]) Suppose that
![]() $a_1a_2e_1e_2\gt b_1b_2$
. Then for every
$a_1a_2e_1e_2\gt b_1b_2$
. Then for every
![]() $ c\in [0, c^\ast )$
, system (1.5) has a unique strictly increasing solution
$ c\in [0, c^\ast )$
, system (1.5) has a unique strictly increasing solution
![]() $(u_c,v_c)\in (C^2(\mathbb{R}^+))^2$
; for
$(u_c,v_c)\in (C^2(\mathbb{R}^+))^2$
; for
![]() $c\geq c^\ast$
, system (1.5) has no such solution. Moreover, for any
$c\geq c^\ast$
, system (1.5) has no such solution. Moreover, for any
![]() $\nu \gt 0$
there exists a unique
$\nu \gt 0$
there exists a unique
![]() $c_\nu \in (0,c^\ast )$
such that
$c_\nu \in (0,c^\ast )$
such that
![]() $u^{\prime}_{c_\nu }(0)=c_\nu/\nu$
.
$u^{\prime}_{c_\nu }(0)=c_\nu/\nu$
.
The solution
![]() $(u_{c_\nu },v_{c_\nu })$
is called a semi-wave with speed
$(u_{c_\nu },v_{c_\nu })$
is called a semi-wave with speed
![]() $c_\nu$
, since
$c_\nu$
, since
![]() $(\mathcal{H},\mathcal{M})(x,t)=(u_{c_\nu },v_{c_\nu })(c_\nu t-x)$
satisfies
$(\mathcal{H},\mathcal{M})(x,t)=(u_{c_\nu },v_{c_\nu })(c_\nu t-x)$
satisfies
 \begin{eqnarray*} \begin{cases} \mathcal{H}_t=d_1 \mathcal{H}_{xx}+a_1(e_1-\mathcal{H})\mathcal{M}-b_1\mathcal{H},& x\lt c_\nu t,\, t\in \mathbb{R},\\ \mathcal{M}_t=d_2 \mathcal{M}_{xx}+a_2(e_2-\mathcal{M})\mathcal{H}-b_2 \mathcal{M}, & x\lt c_\nu t,\, t\in \mathbb{R},\\ (\mathcal{H},\mathcal{M})(\!-\infty,t)=(H^\ast,M^\ast ),& t\in \mathbb{R},\\ (\mathcal{H},\mathcal{M})(c_\nu t,t)=(0,0),\, (c_\nu t)^{\prime}=-\nu \mathcal{H}_x(c_\nu t,t),& t\in \mathbb{R}.\\ \end{cases} \end{eqnarray*}
\begin{eqnarray*} \begin{cases} \mathcal{H}_t=d_1 \mathcal{H}_{xx}+a_1(e_1-\mathcal{H})\mathcal{M}-b_1\mathcal{H},& x\lt c_\nu t,\, t\in \mathbb{R},\\ \mathcal{M}_t=d_2 \mathcal{M}_{xx}+a_2(e_2-\mathcal{M})\mathcal{H}-b_2 \mathcal{M}, & x\lt c_\nu t,\, t\in \mathbb{R},\\ (\mathcal{H},\mathcal{M})(\!-\infty,t)=(H^\ast,M^\ast ),& t\in \mathbb{R},\\ (\mathcal{H},\mathcal{M})(c_\nu t,t)=(0,0),\, (c_\nu t)^{\prime}=-\nu \mathcal{H}_x(c_\nu t,t),& t\in \mathbb{R}.\\ \end{cases} \end{eqnarray*}
When spreading happens for (1.3), by making use of such semi-waves, it is shown in [Reference Wang, Nie and Du33] (see Theorem 3.15 there) that
which means that the asymptotic spreading speed determined by (1.3) is
![]() $c_\nu$
. Thus it is strictly less than that of the corresponding reaction–diffusion system (1.2) (i.e.,
$c_\nu$
. Thus it is strictly less than that of the corresponding reaction–diffusion system (1.2) (i.e.,
![]() $c_\nu \lt c^*$
).Footnote
1
$c_\nu \lt c^*$
).Footnote
1
The purpose of this paper is to provide a more precise description of the spreading profile of the solution to (1.3). We will show that, as
![]() $t\to \infty$
,
$t\to \infty$
,
![]() $h(t)-c_\nu t$
and
$h(t)-c_\nu t$
and
![]() $g(t)+c_\nu t$
converge to some constants, and
$g(t)+c_\nu t$
converge to some constants, and
 \begin{equation*} \begin {cases} \big [H(x,t)-u_{c_\nu }(h(t)-x)\big ]\to 0, \ \big [M(x,t)-v_{c_\nu }(h(t)-x)\big ]\to 0 &\mbox { uniformly for } x\in [0, h(t)],\\ \big [H(x,t)-u_{c_\nu }(x-g(t))\big ]\to 0, \ \big [M(x,t)-v_{c_\nu }(x-g(t))\big ]\to 0 &\mbox { uniformly for } x\in [g(t), 0]. \end {cases} \end{equation*}
\begin{equation*} \begin {cases} \big [H(x,t)-u_{c_\nu }(h(t)-x)\big ]\to 0, \ \big [M(x,t)-v_{c_\nu }(h(t)-x)\big ]\to 0 &\mbox { uniformly for } x\in [0, h(t)],\\ \big [H(x,t)-u_{c_\nu }(x-g(t))\big ]\to 0, \ \big [M(x,t)-v_{c_\nu }(x-g(t))\big ]\to 0 &\mbox { uniformly for } x\in [g(t), 0]. \end {cases} \end{equation*}
Thus, as time goes to infinity, the solution of the free boundary problem (1.3) behaves exactly like the semi-wave.
For a single equation with free boundaries, sharp convergence results of similar nature have been obtained in several recent works; see [Reference Du, Matsuzawa and Zhou11, Reference Du, Wei and Zhou16, Reference Gu, Lou and Zhou18, Reference Kaneko and Matsuzawa20, Reference Kaneko, Matsuzawa and Yamada21, Reference Lei and Du23] for one-dimensional problems and [Reference Du, Matsuzawa and Zhou12] for high-dimensional problems. To the best of our knowledge, there are no results giving such precise asymptotic profiles for systems with free boundary before this work. We believe that the techniques developed in this paper should have applications to some other free boundary systems where similar precise dynamical behaviour is expected.
The mathematical analysis of this paper is inspired by the method of Du, Matsuzawa and Zhou [Reference Du, Matsuzawa and Zhou11, Reference Du, Matsuzawa and Zhou12], but considerable variations are needed as our model here is a system. Moreover, several new techniques are introduced here; see, for example, the proofs of Lemmas 3.4 and 4.2. Some of the new techniques here have the advantage of applicable to more general problems than those in [Reference Du, Matsuzawa and Zhou11, Reference Du, Matsuzawa and Zhou12], where a lower estimate on the solution over a spatial domain of the form
![]() $(\!-ct, ct)$
,
$(\!-ct, ct)$
,
![]() $0\lt c\lt c_\nu$
is required first. Even if it is applied to the same problems in [Reference Du, Matsuzawa and Zhou11, Reference Du, Matsuzawa and Zhou12], the method here yields much simpler proofs.
$0\lt c\lt c_\nu$
is required first. Even if it is applied to the same problems in [Reference Du, Matsuzawa and Zhou11, Reference Du, Matsuzawa and Zhou12], the method here yields much simpler proofs.
Our main result is the following theorem.
Theorem 1.2.
Let
![]() $(H,M,g,h)$
and
$(H,M,g,h)$
and
![]() $(u_{c_\nu },v_{c_\nu }, c_\nu )$
be the solutions of (1.3) and (1.5), respectively. When spreading happens to
$(u_{c_\nu },v_{c_\nu }, c_\nu )$
be the solutions of (1.3) and (1.5), respectively. When spreading happens to
![]() $(H,M,g,h)$
, there exist two constants
$(H,M,g,h)$
, there exist two constants
![]() $g^\ast$
and
$g^\ast$
and
![]() $h^\ast$
such that
$h^\ast$
such that
 \begin{equation} \begin{cases} \lim _{t\rightarrow \infty }(g(t)+c_\nu t-g^\ast )=0,\ \lim _{t\rightarrow \infty }g^{\prime}(t)=-c_\nu,\\ \lim _{t\rightarrow \infty }(h(t)-c_\nu t-h^\ast )=0,\ \lim _{t\rightarrow \infty }h^{\prime}(t)=c_\nu. \end{cases} \end{equation}
\begin{equation} \begin{cases} \lim _{t\rightarrow \infty }(g(t)+c_\nu t-g^\ast )=0,\ \lim _{t\rightarrow \infty }g^{\prime}(t)=-c_\nu,\\ \lim _{t\rightarrow \infty }(h(t)-c_\nu t-h^\ast )=0,\ \lim _{t\rightarrow \infty }h^{\prime}(t)=c_\nu. \end{cases} \end{equation}
Moreover,
 \begin{equation} \begin{cases}\lim _{t\rightarrow \infty }\|\left (H(\cdot,t),M(\cdot,t)\right )-\left (u_{c_\nu }(\!\cdot -g(t)), v_{c_\nu }(\!\cdot -g(t))\right )\|_{L^\infty ([g(t),0])}=0,\\ \lim _{t\rightarrow \infty }\|\left (H(\cdot,t),M(\cdot,t)\right )-\left (u_{c_\nu }(h(t)-\cdot ), v_{c_\nu }(h(t)-\cdot )\right )\|_{L^\infty ([0,h(t)])}=0. \end{cases} \end{equation}
\begin{equation} \begin{cases}\lim _{t\rightarrow \infty }\|\left (H(\cdot,t),M(\cdot,t)\right )-\left (u_{c_\nu }(\!\cdot -g(t)), v_{c_\nu }(\!\cdot -g(t))\right )\|_{L^\infty ([g(t),0])}=0,\\ \lim _{t\rightarrow \infty }\|\left (H(\cdot,t),M(\cdot,t)\right )-\left (u_{c_\nu }(h(t)-\cdot ), v_{c_\nu }(h(t)-\cdot )\right )\|_{L^\infty ([0,h(t)])}=0. \end{cases} \end{equation}
We would like to further remark that the ODE version of (1.1) is widely known as the Ross–Macdonold model due to the early works of Ross [Reference Ross28] and Macdonald [Reference Macdonald27] on malaria, whose spreading relies on mosquito as a vector and human as a host. There is an extensive literature on the modelling of epidemic spreading by using various variations of the Ross–Macdonald model; see, for example, [Reference Lou and Zhao26, Reference Wang, Qiang and Wang30] and the references therein. As a consequence, the mathematical results above are applicable to suitable free boundary versions of the Ross–Macdonold model as well.
Finally, we mention some more related works on WNv models with free boundary. Tarboush et al. [Reference Tarboush, Lin and Zhang29] obtain a vanishing–spreading dichotomy for a similar model, where the equation for birds is a PDE while the equation for mosquitoes is an ODE; Cheng and Zheng [Reference Cheng and Zheng5] studied the dynamics and spreading speed of (1.3) with an advection term. However, the asymptotic profiles for these models have not been determined. To include long-distance dispersal of the virus, a WNv model with non-local diffusion and free boundaries is proposed and analysed very recently by Du and Ni [Reference Du and Ni13–Reference Du and Ni15]. But due to certain technical obstacles, no convergence result of the type as described in Theorem 1.2 above is available for such non-local diffusion models. Some further related recent work in this direction can be found in the review papers of Du [Reference Du6, Reference Du7].
The rest of this paper is organised as follows. In Section 2, we collect some basic results including some comparison principles, rough estimate of solutions to (1.3) and the asymptotic behaviours of semi-wave solutions of (1.5). In Section 3, we show that
![]() $|g(t)+c_\nu t|$
and
$|g(t)+c_\nu t|$
and
![]() $|h(t)-c_\nu t|$
are both bounded for all
$|h(t)-c_\nu t|$
are both bounded for all
![]() $t\gt 0$
; as mentioned earlier, we have to overcome several non-trivial difficulties here. In Section 4, we finish the proof of Theorem 1.2, where our arguments are based on the estimates obtained in Section 3 and on the construction of suitable upper and lower solutions.
$t\gt 0$
; as mentioned earlier, we have to overcome several non-trivial difficulties here. In Section 4, we finish the proof of Theorem 1.2, where our arguments are based on the estimates obtained in Section 3 and on the construction of suitable upper and lower solutions.
2. Some preparations
In this section, we prepare some basic results. Firstly, we introduce some notations that will be used throughout this paper. For any vectors
![]() $\textbf{p}=(p_1,p_2,\ldots,p_m),\textbf{q}=(q_1,q_2,\ldots,q_m)\in \mathbb{R}^m$
,
$\textbf{p}=(p_1,p_2,\ldots,p_m),\textbf{q}=(q_1,q_2,\ldots,q_m)\in \mathbb{R}^m$
,
![]() $\textbf{p}\preceq (\succeq ) \textbf{q}$
(resp.,
$\textbf{p}\preceq (\succeq ) \textbf{q}$
(resp.,
![]() $\textbf{p}\prec (\succ )\textbf{q}$
) means
$\textbf{p}\prec (\succ )\textbf{q}$
) means
![]() $p_i\leq (\geq )q_i$
(resp.,
$p_i\leq (\geq )q_i$
(resp.,
![]() $p_i\lt (\gt )q_i$
) for
$p_i\lt (\gt )q_i$
) for
![]() $1\leq i\leq m$
. Any
$1\leq i\leq m$
. Any
![]() $B\,:\!=(b_{ij})\in \mathbb{R}^m\times \mathbb{R}^n$
is a matrix with
$B\,:\!=(b_{ij})\in \mathbb{R}^m\times \mathbb{R}^n$
is a matrix with
![]() $m$
rows and
$m$
rows and
![]() $n$
columns, whose transpose is denoted by
$n$
columns, whose transpose is denoted by
![]() $B^\top$
.
$B^\top$
.
The following comparison principles for the free boundary problem (1.3) will be used. They are simple variations of Proposition 3.13 of [Reference Wang, Nie and Du33] and can be proved by arguments similar to those used in the proof of Lemma 2.6 in [Reference Du and Lin10].
Lemma 2.1.
Let
![]() $(H,M,g, h)$
be the solution of (1.3). Assume that
$(H,M,g, h)$
be the solution of (1.3). Assume that
![]() $T\in (0,\infty )$
,
$T\in (0,\infty )$
,
![]() $\overline g, \overline{h}\in C^1([0,T])$
,
$\overline g, \overline{h}\in C^1([0,T])$
,
![]() $g(t)\leq \overline g(t)\lt \overline h(t)$
in
$g(t)\leq \overline g(t)\lt \overline h(t)$
in
![]() $[0, T]$
,
$[0, T]$
,
![]() $\overline{H},\overline{M}\in C(\overline{D_T^{\ast }})\cap C^{2,1}(D_T^{\ast })$
with
$\overline{H},\overline{M}\in C(\overline{D_T^{\ast }})\cap C^{2,1}(D_T^{\ast })$
with
![]() $D_T^{\ast }=\{(x,t)\in \mathbb{R}^2:x\in (\overline g(t),\overline{h}(t)),t\in (0,T]\}$
, and
$D_T^{\ast }=\{(x,t)\in \mathbb{R}^2:x\in (\overline g(t),\overline{h}(t)),t\in (0,T]\}$
, and
 \begin{eqnarray} \begin{cases} \overline{H}_t-d_1\overline{H}_{xx}\geq a_1(e_1-\overline{H})\overline{M}-b_1\overline{H},\,& \overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{M}_t-d_2\overline{M}_{xx}\geq a_2(e_2-\overline{M})\overline{H}-b_2\overline{M},\,&\overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{H}(x,t)\geq H(x,t),\,\overline M(x,t)\geq M(x, t),\,& x=\overline g(t),\ 0\lt t\lt T,\\ \overline{H}(x,t)=\overline{M}(x,t)=0,\,& x=\overline{h}(t),\,0\lt t\lt T,\\ \overline{h}^{\prime}(t)\geq -\nu \overline{H}_x(\overline{h}(t),t),\,&0\lt t\lt T,\\ \overline{H}(x,0)\geq H_{0}(x),\, \overline{M}(x,0)\geq M_{0}(x),\,&\overline g(0)\leq x\leq h_0. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \overline{H}_t-d_1\overline{H}_{xx}\geq a_1(e_1-\overline{H})\overline{M}-b_1\overline{H},\,& \overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{M}_t-d_2\overline{M}_{xx}\geq a_2(e_2-\overline{M})\overline{H}-b_2\overline{M},\,&\overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{H}(x,t)\geq H(x,t),\,\overline M(x,t)\geq M(x, t),\,& x=\overline g(t),\ 0\lt t\lt T,\\ \overline{H}(x,t)=\overline{M}(x,t)=0,\,& x=\overline{h}(t),\,0\lt t\lt T,\\ \overline{h}^{\prime}(t)\geq -\nu \overline{H}_x(\overline{h}(t),t),\,&0\lt t\lt T,\\ \overline{H}(x,0)\geq H_{0}(x),\, \overline{M}(x,0)\geq M_{0}(x),\,&\overline g(0)\leq x\leq h_0. \end{cases} \end{eqnarray}
Then
Lemma 2.2.
Let
![]() $(H,M,g, h)$
be the solution of (1.3). Assume that
$(H,M,g, h)$
be the solution of (1.3). Assume that
![]() $T\in (0,\infty )$
,
$T\in (0,\infty )$
,
![]() $\overline g\lt \overline{h}$
are functions in
$\overline g\lt \overline{h}$
are functions in
![]() $ C^1([0,T])$
,
$ C^1([0,T])$
,
![]() $\overline{H},\overline{M}\in C(\overline{D_T^{\ast }})\cap C^{2,1}(D_T^{\ast })$
with
$\overline{H},\overline{M}\in C(\overline{D_T^{\ast }})\cap C^{2,1}(D_T^{\ast })$
with
![]() $D_T^{\ast }=\{(x,t)\in \mathbb{R}^2:x\in (\overline g(t),\overline{h}(t)),t\in (0,T]\}$
, and
$D_T^{\ast }=\{(x,t)\in \mathbb{R}^2:x\in (\overline g(t),\overline{h}(t)),t\in (0,T]\}$
, and
 \begin{eqnarray} \begin{cases} \overline{H}_t-d_1\overline{H}_{xx}\geq a_1(e_1-\overline{H})\overline{M}-b_1\overline{H},\,& \overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{M}_t-d_2\overline{M}_{xx}\geq a_2(e_2-\overline{M})\overline{H}-b_2\overline{M},\,&\overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{H}(x,t)=\overline{M}(x,t)=0,\,& x=\overline g(t) \mbox{ or } \overline{h}(t),\,0\lt t\lt T,\\ \overline{g}^{\prime}(t)\leq -\nu \overline{H}_x(\overline{g}(t),t),\ \overline{h}^{\prime}(t)\geq -\nu \overline{H}_x(\overline{h}(t),t),\,&0\lt t\lt T,\\ \overline{H}(x,0)\geq H_{0}(x),\, \overline{M}(x,0)\geq M_{0}(x),\,&-h_0\leq x\leq h_0. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \overline{H}_t-d_1\overline{H}_{xx}\geq a_1(e_1-\overline{H})\overline{M}-b_1\overline{H},\,& \overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{M}_t-d_2\overline{M}_{xx}\geq a_2(e_2-\overline{M})\overline{H}-b_2\overline{M},\,&\overline g(t)\lt x\lt \overline{h}(t),\,0\lt t\lt T,\\ \overline{H}(x,t)=\overline{M}(x,t)=0,\,& x=\overline g(t) \mbox{ or } \overline{h}(t),\,0\lt t\lt T,\\ \overline{g}^{\prime}(t)\leq -\nu \overline{H}_x(\overline{g}(t),t),\ \overline{h}^{\prime}(t)\geq -\nu \overline{H}_x(\overline{h}(t),t),\,&0\lt t\lt T,\\ \overline{H}(x,0)\geq H_{0}(x),\, \overline{M}(x,0)\geq M_{0}(x),\,&-h_0\leq x\leq h_0. \end{cases} \end{eqnarray}
Then
Remark 2.3. (i) If the reverse inequalities in (2.1) hold, and
![]() $(\overline{H},\overline{M},\overline{g},\overline{h})$
is rewritten as
$(\overline{H},\overline{M},\overline{g},\overline{h})$
is rewritten as
![]() $(\underline{H},\underline{M},\underline{g},\underline{h})$
, then
$(\underline{H},\underline{M},\underline{g},\underline{h})$
, then
(ii) Similarly, if the reverse inequalities in (2.2) hold, and
![]() $(\overline{H},\overline{M},\overline{g},\overline{h})$
is rewritten as
$(\overline{H},\overline{M},\overline{g},\overline{h})$
is rewritten as
![]() $(\underline{H},\underline{M},\underline{g},\underline{h})$
, then
$(\underline{H},\underline{M},\underline{g},\underline{h})$
, then
(iii) The functions
![]() $(\overline{H},\overline{M},\overline{g},\overline{h})$
and
$(\overline{H},\overline{M},\overline{g},\overline{h})$
and
![]() $(\underline{H},\underline{M},\underline{g},\underline{h})$
are usually called an upper solution and a lower solution of (1.3), respectively.
$(\underline{H},\underline{M},\underline{g},\underline{h})$
are usually called an upper solution and a lower solution of (1.3), respectively.
The global existence and uniqueness of a positive solution to (1.3) have been obtained in [Reference Lin and Zhu25]. The following estimates on such solutions are needed later in the paper.
Lemma 2.4. (Theorem 3.1 of [Reference Lin and Zhu25]) Suppose
![]() $(H,M,g,h)$
is the solution to (1.3). Then
$(H,M,g,h)$
is the solution to (1.3). Then
Moreover, there exists
![]() $C_0\gt 0$
such that
$C_0\gt 0$
such that
By Lemma 3.8 and its proof in [Reference Wang, Nie and Du33], we have the following result:
Lemma 2.5.
Let
![]() $(u(s),v(s))$
be a monotone solution of (1.5). Then there exist constants
$(u(s),v(s))$
be a monotone solution of (1.5). Then there exist constants
![]() $\hat \mu _1\lt 0$
,
$\hat \mu _1\lt 0$
,
![]() $p\gt 0$
and
$p\gt 0$
and
![]() $q\gt 0$
such that, as
$q\gt 0$
such that, as
![]() $s\rightarrow \infty$
,
$s\rightarrow \infty$
,
 \begin{eqnarray} \begin{cases} (u(s),v(s))=(H^\ast,M^\ast )- e^{\hat{\mu }_1s}(p+o(1),q+o(1)),\\ (u^{\prime}(s), v^{\prime}(s))=O(e^{\hat{\mu }_1s} ). \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} (u(s),v(s))=(H^\ast,M^\ast )- e^{\hat{\mu }_1s}(p+o(1),q+o(1)),\\ (u^{\prime}(s), v^{\prime}(s))=O(e^{\hat{\mu }_1s} ). \end{cases} \end{eqnarray}
3. Bounds for
 $\boldsymbol{g}(\boldsymbol{t})+\boldsymbol{c}_{\boldsymbol{\nu}} \boldsymbol{t}$
and
$\boldsymbol{g}(\boldsymbol{t})+\boldsymbol{c}_{\boldsymbol{\nu}} \boldsymbol{t}$
and
 $\boldsymbol{h}(\boldsymbol{t})-\boldsymbol{c}_{\boldsymbol{\nu}} \boldsymbol{t}$
$\boldsymbol{h}(\boldsymbol{t})-\boldsymbol{c}_{\boldsymbol{\nu}} \boldsymbol{t}$
In this section, we show that when spreading happens, both
![]() $g(t)+c_\nu t$
and
$g(t)+c_\nu t$
and
![]() $h(t)-c_\nu t$
are bounded functions for
$h(t)-c_\nu t$
are bounded functions for
![]() $t\gt 0$
. More precisely, we will prove the following result:
$t\gt 0$
. More precisely, we will prove the following result:
Proposition 3.1.
Suppose that spreading happens to the solution
![]() $(H,M,g,h)$
of (1.3). Then there exists a positive constant
$(H,M,g,h)$
of (1.3). Then there exists a positive constant
![]() $C$
such that
$C$
such that
We will prove this result by constructing suitable upper and lower solutions, in the spirit of Fife and McLeod [Reference Fife and McLeod17], except that now we are dealing with a system of equations and the associated semi-waves are used.
3.1. Upper bound
In this subsection, we obtain an upper bound for
![]() $(H,M,g,h)$
by constructing an upper solution
$(H,M,g,h)$
by constructing an upper solution
![]() $(\overline{H},\overline{M},\bar{g},\bar{h})$
to (1.3) as follows:
$(\overline{H},\overline{M},\bar{g},\bar{h})$
to (1.3) as follows:
where
![]() $T^\ast$
,
$T^\ast$
,
![]() $K_1,X_0,\delta,\sigma$
are positive constants to be determined later.
$K_1,X_0,\delta,\sigma$
are positive constants to be determined later.
Lemma 3.2.
For any given constants
![]() $T^*\gt 0$
and
$T^*\gt 0$
and
![]() $X_0\gt 0$
, there exist positive constants
$X_0\gt 0$
, there exist positive constants
![]() $K_1, \delta$
and
$K_1, \delta$
and
![]() $\sigma$
, such that the solution
$\sigma$
, such that the solution
![]() $(H,M,h)$
to (1.3) satisfies, for
$(H,M,h)$
to (1.3) satisfies, for
![]() $x\in [g(t),h(t)]\mbox{ and }t\gt T^\ast$
,
$x\in [g(t),h(t)]\mbox{ and }t\gt T^\ast$
,
Proof. We claim that
![]() $(\overline{H},\overline{M},\bar{g},\bar{h})$
is an upper solution for
$(\overline{H},\overline{M},\bar{g},\bar{h})$
is an upper solution for
![]() $t\gt T^\ast$
by taking appropriate parameters
$t\gt T^\ast$
by taking appropriate parameters
![]() $T^*,K_1,X_0,\delta$
and
$T^*,K_1,X_0,\delta$
and
![]() $\sigma$
, that is,
$\sigma$
, that is,
If the above inequalities are verified, then we can apply Lemma 2.1 to conclude that (3.2) holds, and hence the proof is completed.
We now verify the inequalities (3.3)–(3.8). Firstly, it is clear that
![]() $(H,M)(\bar{g}(t),t)=(H,M)(g(t),t)$
$(H,M)(\bar{g}(t),t)=(H,M)(g(t),t)$
![]() $=(0,0)$
and
$=(0,0)$
and
![]() $(\overline{H},\overline{M})(\bar{g}(t),t)\succ (0,0)$
for
$(\overline{H},\overline{M})(\bar{g}(t),t)\succ (0,0)$
for
![]() $t\gt T^\ast$
. Thus, (3.5) holds.
$t\gt T^\ast$
. Thus, (3.5) holds.
It is obvious that
![]() $(\overline{H},\overline{M})(\bar{h}(t),t)=(0,0)$
and
$(\overline{H},\overline{M})(\bar{h}(t),t)=(0,0)$
and
![]() $\bar{h}(T^\ast )=h(T^\ast )+X_0\gt h(T^\ast )$
. Moreover, direct computation gives that
$\bar{h}(T^\ast )=h(T^\ast )+X_0\gt h(T^\ast )$
. Moreover, direct computation gives that
and
Hence, (3.6) and (3.7) hold provided that
Since
![]() $X_0\gt 0$
, for all large
$X_0\gt 0$
, for all large
![]() $K_1$
(depending on
$K_1$
(depending on
![]() $X_0$
), say
$X_0$
), say
![]() $K_1\geq C(X_0)\gt 0$
, we have
$K_1\geq C(X_0)\gt 0$
, we have
Hence, due to Lemma 2.4, we have, for
![]() $x\in [\overline{g}(T^\ast ),h(T^\ast )]$
,
$x\in [\overline{g}(T^\ast ),h(T^\ast )]$
,
 \begin{eqnarray*} \begin{aligned} \overline{H}(x,T^\ast )&=(1+K_1)u_{c_\nu }(\bar{h}(T^\ast )-x)\\ &=(1+K_1)u_{c_\nu }(h(T^\ast )+X_0-x)\\ &\geq (1+K_1)u_{c_\nu }(X_0)\geq e_1\\ &\geq H(x,T^\ast ). \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} \overline{H}(x,T^\ast )&=(1+K_1)u_{c_\nu }(\bar{h}(T^\ast )-x)\\ &=(1+K_1)u_{c_\nu }(h(T^\ast )+X_0-x)\\ &\geq (1+K_1)u_{c_\nu }(X_0)\geq e_1\\ &\geq H(x,T^\ast ). \end{aligned} \end{eqnarray*}
A similar argument gives
![]() $\overline{M}(x,T^\ast )\geq M(x,T^\ast )$
for
$\overline{M}(x,T^\ast )\geq M(x,T^\ast )$
for
![]() $x\in [\overline{g}(T^\ast ),h(T^\ast )]$
. Hence, (3.8) holds true.
$x\in [\overline{g}(T^\ast ),h(T^\ast )]$
. Hence, (3.8) holds true.
Finally, we show (3.3) and (3.4). Let
![]() $s=\bar{h}(t)-x$
. Then,
$s=\bar{h}(t)-x$
. Then,
 \begin{eqnarray*} \begin{aligned} \overline{H}_t(x,t)&=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }^{\prime}(s)\bar{h}^{\prime}(t)\\ &=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})(c_\nu +\sigma \delta e^{-\delta (t-T^*)})u_{c_\nu }^{\prime}(s),\\ \overline{M}_t(x,t)&=-\delta K_1e^{-\delta (t-T^*)}v_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})v_{c_\nu }^{\prime}(s)\bar{h}^{\prime}(t)\\ &=-\delta K_1e^{-\delta (t-T^*)}v_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})(c_\nu +\sigma \delta e^{-\delta (t-T^*)})v_{c_\nu }^{\prime}(s) \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} \overline{H}_t(x,t)&=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }^{\prime}(s)\bar{h}^{\prime}(t)\\ &=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})(c_\nu +\sigma \delta e^{-\delta (t-T^*)})u_{c_\nu }^{\prime}(s),\\ \overline{M}_t(x,t)&=-\delta K_1e^{-\delta (t-T^*)}v_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})v_{c_\nu }^{\prime}(s)\bar{h}^{\prime}(t)\\ &=-\delta K_1e^{-\delta (t-T^*)}v_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})(c_\nu +\sigma \delta e^{-\delta (t-T^*)})v_{c_\nu }^{\prime}(s) \end{aligned} \end{eqnarray*}
and
Therefore,
 \begin{eqnarray*} \begin{aligned} &\overline{H}_t- d_1 \overline{H}_{xx}-a_1(e_1-\overline{H})\overline{M}+b_1 \overline{H}\\ &\quad=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})(c_\nu +\sigma \delta e^{-\delta (t-T^*)})u_{c_\nu }^{\prime}(s)\\ &\qquad-d_1 (1+K_1e^{-\delta (t-T^*)})u_{c_\nu }^{\prime\prime}(s)\\ &\qquad-a_1[e_1-(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)](1+K_1e^{-\delta (t-T^*)})v_{c_\nu }(s)+b_1(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)\\ &\quad=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})\sigma \delta e^{-\delta (t-T^*)}u_{c_\nu }^{\prime}(s)\\ &\qquad+(1+K_1e^{-\delta (t-T^*)})\big [c_\nu u_{c_\nu }^{\prime}(s)-d_1u_{c_\nu }^{\prime\prime}(s)\big ]\\ &\qquad-a_1[e_1-(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)](1+K_1e^{-\delta (t-T^*)})v_{c_\nu }(s)+b_1(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)\\ &\quad=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})\sigma \delta e^{-\delta (t-T^*)}u_{c_\nu }^{\prime}(s)\\ &\qquad+(1+K_1e^{-\delta (t-T^*)})[a_1(e_1-u_{c_\nu }(s))v_{c_\nu }(s)-b_1u_{c_\nu }(s)]\\ &\qquad-a_1[e_1-(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)](1+K_1e^{-\delta (t-T^*)})v_{c_\nu }(s)+b_1(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)\\ &\quad=\ e^{-\delta (t-T^*)}\Big [\!-\delta K_1u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})\sigma \delta u_{c_\nu }^{\prime}(s) +a_1K_1u_{c_\nu }(s)v_{c_\nu }(s)(1+K_1e^{-\delta (t-T^*)})\Big ]. \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} &\overline{H}_t- d_1 \overline{H}_{xx}-a_1(e_1-\overline{H})\overline{M}+b_1 \overline{H}\\ &\quad=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})(c_\nu +\sigma \delta e^{-\delta (t-T^*)})u_{c_\nu }^{\prime}(s)\\ &\qquad-d_1 (1+K_1e^{-\delta (t-T^*)})u_{c_\nu }^{\prime\prime}(s)\\ &\qquad-a_1[e_1-(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)](1+K_1e^{-\delta (t-T^*)})v_{c_\nu }(s)+b_1(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)\\ &\quad=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})\sigma \delta e^{-\delta (t-T^*)}u_{c_\nu }^{\prime}(s)\\ &\qquad+(1+K_1e^{-\delta (t-T^*)})\big [c_\nu u_{c_\nu }^{\prime}(s)-d_1u_{c_\nu }^{\prime\prime}(s)\big ]\\ &\qquad-a_1[e_1-(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)](1+K_1e^{-\delta (t-T^*)})v_{c_\nu }(s)+b_1(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)\\ &\quad=-\delta K_1e^{-\delta (t-T^*)}u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})\sigma \delta e^{-\delta (t-T^*)}u_{c_\nu }^{\prime}(s)\\ &\qquad+(1+K_1e^{-\delta (t-T^*)})[a_1(e_1-u_{c_\nu }(s))v_{c_\nu }(s)-b_1u_{c_\nu }(s)]\\ &\qquad-a_1[e_1-(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)](1+K_1e^{-\delta (t-T^*)})v_{c_\nu }(s)+b_1(1+K_1e^{-\delta (t-T^*)})u_{c_\nu }(s)\\ &\quad=\ e^{-\delta (t-T^*)}\Big [\!-\delta K_1u_{c_\nu }(s)+(1+K_1e^{-\delta (t-T^*)})\sigma \delta u_{c_\nu }^{\prime}(s) +a_1K_1u_{c_\nu }(s)v_{c_\nu }(s)(1+K_1e^{-\delta (t-T^*)})\Big ]. \end{aligned} \end{eqnarray*}
Since
we have
Define
Then
![]() $A, \, B_1$
,
$A, \, B_1$
,
![]() $B_2\gt 0$
and
$B_2\gt 0$
and
 \begin{equation*} -\delta K_1 H^*+\sigma \delta u_{c_\nu }^{\prime}(s) +a_1K_1u_{c_\nu }(s)v_{c_\nu }(s) \geq \begin {cases} -\delta K_1 H^*+\sigma \delta B_1 & \mbox { for } s\in [0,1],\\ -\delta K_1 H^*+a_1K_1 A& \mbox { for } s\geq 1. \end {cases} \end{equation*}
\begin{equation*} -\delta K_1 H^*+\sigma \delta u_{c_\nu }^{\prime}(s) +a_1K_1u_{c_\nu }(s)v_{c_\nu }(s) \geq \begin {cases} -\delta K_1 H^*+\sigma \delta B_1 & \mbox { for } s\in [0,1],\\ -\delta K_1 H^*+a_1K_1 A& \mbox { for } s\geq 1. \end {cases} \end{equation*}
Therefore, (3.3) holds provided that
Moreover, by parallel arguments we see that (3.4) holds provided that additionally
Now for any given
![]() $X_0\gt 0$
and
$X_0\gt 0$
and
![]() $T^*\gt 0$
, we can choose
$T^*\gt 0$
, we can choose
![]() $\sigma, \delta, K_1$
such that (3.9), (3.10), (3.12) and (3.13) hold simultaneously; for example, we may first choose
$\sigma, \delta, K_1$
such that (3.9), (3.10), (3.12) and (3.13) hold simultaneously; for example, we may first choose
![]() $K_1$
large satisfying (3.10) and then choose
$K_1$
large satisfying (3.10) and then choose
![]() $\delta \gt 0$
small and choose
$\delta \gt 0$
small and choose
![]() $\sigma$
large such that (3.9), (3.12) and (3.13) hold. The proof is now complete.
$\sigma$
large such that (3.9), (3.12) and (3.13) hold. The proof is now complete.
3.2. Lower bound
The lower bound will be obtained by constructing a lower solution
![]() $(\underline{H},\underline{M},\underline{g},\underline{h})$
to (1.3). Set
$(\underline{H},\underline{M},\underline{g},\underline{h})$
to (1.3). Set
 \begin{equation} \begin{aligned} \underline{g}(t)&=-\underline h (t), \ \underline{h}(t)=c_\nu (t-T_\ast )+L-(1-e^{-\delta (t-T_*)}),\\ \underline{H}(x,t)&=(1-\tilde \epsilon e^{-\delta (t-T_*)})\big [u_{c_\nu }(\underline{h}(t)-x)+u_{c_\nu }(\underline{h}(t)+x)-u_{c_\nu }(2\underline{h}(t))\big ],\\ \underline{M}(x,t)&=(1-\tilde \epsilon e^{-\delta (t-T_*)})\big [ v_{c_\nu }(\underline{h}(t)-x)+v_{c_\nu }(\underline{h}(t)+x)-v_{c_\nu }(2\underline{h}(t))\big ], \end{aligned} \end{equation}
\begin{equation} \begin{aligned} \underline{g}(t)&=-\underline h (t), \ \underline{h}(t)=c_\nu (t-T_\ast )+L-(1-e^{-\delta (t-T_*)}),\\ \underline{H}(x,t)&=(1-\tilde \epsilon e^{-\delta (t-T_*)})\big [u_{c_\nu }(\underline{h}(t)-x)+u_{c_\nu }(\underline{h}(t)+x)-u_{c_\nu }(2\underline{h}(t))\big ],\\ \underline{M}(x,t)&=(1-\tilde \epsilon e^{-\delta (t-T_*)})\big [ v_{c_\nu }(\underline{h}(t)-x)+v_{c_\nu }(\underline{h}(t)+x)-v_{c_\nu }(2\underline{h}(t))\big ], \end{aligned} \end{equation}
where
![]() $T_\ast$
,
$T_\ast$
,
![]() $\tilde \epsilon \in (0, 1),\delta, L$
are positive constants to be determined later.
$\tilde \epsilon \in (0, 1),\delta, L$
are positive constants to be determined later.
We will need the following result from [Reference Du and Ni15]:
Lemma 3.3.
Suppose that
![]() $F=(f_i)\in C^2({\mathbb R}^m,{\mathbb R}^m)$
,
$F=(f_i)\in C^2({\mathbb R}^m,{\mathbb R}^m)$
,
![]() $\mathbf{u}^*\succ 0$
and
$\mathbf{u}^*\succ 0$
and
Then there exists
![]() $\delta _0\gt 0$
small such that for
$\delta _0\gt 0$
small such that for
![]() $0\lt \epsilon \ll 1$
and
$0\lt \epsilon \ll 1$
and
![]() $\mathbf u, \mathbf v\in [(1-\delta _0)\mathbf{u}^*, \mathbf{u}^*]$
satisfying
$\mathbf u, \mathbf v\in [(1-\delta _0)\mathbf{u}^*, \mathbf{u}^*]$
satisfying
we have
We will use this lemma with
![]() $ \mathbf u^*\,:\!=(H^*, M^*)$
and
$ \mathbf u^*\,:\!=(H^*, M^*)$
and
which is easily checked to satisfy (3.15).
Lemma 3.4.
For some suitable choice of
![]() $T_\ast$
,
$T_\ast$
,
![]() $\tilde \epsilon \in (0, 1), \delta$
and
$\tilde \epsilon \in (0, 1), \delta$
and
![]() $ L$
, the solution
$ L$
, the solution
![]() $(H,M,g,h)$
of (1.3) satisfies, for
$(H,M,g,h)$
of (1.3) satisfies, for
![]() $x\in [\underline{g}(t),\underline{h}(t)]$
and
$x\in [\underline{g}(t),\underline{h}(t)]$
and
![]() $t\gt T_\ast$
,
$t\gt T_\ast$
,
Proof. We show that
![]() $(\underline{H},\underline{M},\underline{g},\underline{h})$
is a lower solution for
$(\underline{H},\underline{M},\underline{g},\underline{h})$
is a lower solution for
![]() $t\gt T_\ast$
by taking appropriate parameters
$t\gt T_\ast$
by taking appropriate parameters
![]() $T_\ast$
,
$T_\ast$
,
![]() $\tilde \epsilon \in (0, 1),\delta$
and
$\tilde \epsilon \in (0, 1),\delta$
and
![]() $L$
, namely
$L$
, namely
If the above inequalities are verified, then we can apply Remark 2.3 (ii) to conclude that (3.16) holds, and hence the proof is completed. Note that since
![]() $\underline H(x,t)$
is even in
$\underline H(x,t)$
is even in
![]() $x$
and
$x$
and
![]() $\underline g(t)=-\underline h(t)$
, (3.20) implies
$\underline g(t)=-\underline h(t)$
, (3.20) implies
![]() $\underline g^{\prime}(t)\geq -\nu \underline{H}_{x}(\underline{g}(t),t)$
.
$\underline g^{\prime}(t)\geq -\nu \underline{H}_{x}(\underline{g}(t),t)$
.
We now verify the inequalities (3.17)–(3.21). Since spreading happens, for
![]() $T_*=T_*(L, \tilde \epsilon )$
large enough, we have
$T_*=T_*(L, \tilde \epsilon )$
large enough, we have
and
It is obvious that
![]() $(\underline{H},\underline{M})(\pm \underline{h}(t),t)=(0,0)$
. Direct calculations yield
$(\underline{H},\underline{M})(\pm \underline{h}(t),t)=(0,0)$
. Direct calculations yield
and
 \begin{align*} -\nu \underline{H}_{x}(\underline{h}(t),t)&=\nu (1-\tilde{\epsilon }e^{-\delta (t-T_*)})\big [u_{c_\nu }^{\prime}(0)-u_{c_\nu }^{\prime}(2\underline h(t))\big ]\\ &\geq c_\nu (1-\tilde{\epsilon }e^{-\delta (t-T_*)})-C e^{2 \hat \mu _1 \underline h(t)}\\ &\geq c_\nu - c_\nu \tilde{\epsilon }e^{-\delta (t-T_*)}-C e^{2|\hat \mu _1|(1-L)}e^{2\hat \mu _1 c_\nu (t-T_*)} \end{align*}
\begin{align*} -\nu \underline{H}_{x}(\underline{h}(t),t)&=\nu (1-\tilde{\epsilon }e^{-\delta (t-T_*)})\big [u_{c_\nu }^{\prime}(0)-u_{c_\nu }^{\prime}(2\underline h(t))\big ]\\ &\geq c_\nu (1-\tilde{\epsilon }e^{-\delta (t-T_*)})-C e^{2 \hat \mu _1 \underline h(t)}\\ &\geq c_\nu - c_\nu \tilde{\epsilon }e^{-\delta (t-T_*)}-C e^{2|\hat \mu _1|(1-L)}e^{2\hat \mu _1 c_\nu (t-T_*)} \end{align*}
for some
![]() $C\gt 0$
due to (2.3). We now fix
$C\gt 0$
due to (2.3). We now fix
and obtain
provided that
which holds when
![]() $\tilde \epsilon \gt 0$
is sufficiently small and
$\tilde \epsilon \gt 0$
is sufficiently small and
![]() $L$
is sufficiently large. Hence, (3.19), (3.20) and (3.21) hold.
$L$
is sufficiently large. Hence, (3.19), (3.20) and (3.21) hold.
Finally, we check (3.17) and (3.18). Clearly, writing
![]() $\epsilon =\epsilon (t)\,:\!=\tilde{\epsilon }e^{-\delta (t-T_*)}$
, we have
$\epsilon =\epsilon (t)\,:\!=\tilde{\epsilon }e^{-\delta (t-T_*)}$
, we have
 \begin{eqnarray*} \begin{aligned} \underline{H}_t(x,t)&=\delta \epsilon \big [u_{c_\nu }(\underline h(t)-x) +u_{c_\nu }(\underline h(t)+x)-u_{c_\nu }(2\underline h(t))\big ]\\ & \quad +(1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})\big [u_{c_\nu }^{\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime}(\underline h(t)+x)-2u_{c_\nu }^{\prime}(2\underline h(t))\big ], \\ \underline{M}_t(x,t)&=\delta \epsilon \big [v_{c_\nu }(\underline h(t)-x) +v_{c_\nu }(\underline h(t)+x)-v_{c_\nu }(2\underline h(t))\big ]\\ & \quad +(1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})\big [v_{c_\nu }^{\prime}(\underline h(t)-x) +v_{c_\nu }^{\prime}(\underline h(t)+x)-2v_{c_\nu }^{\prime}(2\underline h(t))\big ] \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} \underline{H}_t(x,t)&=\delta \epsilon \big [u_{c_\nu }(\underline h(t)-x) +u_{c_\nu }(\underline h(t)+x)-u_{c_\nu }(2\underline h(t))\big ]\\ & \quad +(1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})\big [u_{c_\nu }^{\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime}(\underline h(t)+x)-2u_{c_\nu }^{\prime}(2\underline h(t))\big ], \\ \underline{M}_t(x,t)&=\delta \epsilon \big [v_{c_\nu }(\underline h(t)-x) +v_{c_\nu }(\underline h(t)+x)-v_{c_\nu }(2\underline h(t))\big ]\\ & \quad +(1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})\big [v_{c_\nu }^{\prime}(\underline h(t)-x) +v_{c_\nu }^{\prime}(\underline h(t)+x)-2v_{c_\nu }^{\prime}(2\underline h(t))\big ] \end{aligned} \end{eqnarray*}
and
Therefore,
 \begin{eqnarray*} \begin{aligned} &\underline{H}_t- d_1\underline{H}_{xx}-f(\underline H, \underline M)\\ &\quad=\delta \epsilon \big [u_{c_\nu }(\underline h(t)-x) +u_{c_\nu }(\underline h(t)+x)-u_{c_\nu }(2\underline h(t))\big ]\\ &\quad \ \ \ +(1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})\big [u_{c_\nu }^{\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime}(\underline h(t)+x)-2u_{c_\nu }^{\prime}(2\underline h(t))\big ] \\ &\quad\ \ \ -d_1(1-\epsilon )\big [u_{c_\nu }^{\prime\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime\prime}(\underline h(t)+x)\big ]-f(\underline H, \underline M)\\ &\quad= \delta \epsilon \big [u_{c_\nu }(\underline h(t)-x) +u_{c_\nu }(\underline h(t)+x)-u_{c_\nu }(2\underline h(t))\big ]\\ &\quad \ \ \ +(1-\epsilon )\big [ f(u_{c_\nu }(\underline h-x),v_{c_\nu }(\underline h-x))+f(u_{c_\nu }(\underline h+x), v_{c_\nu }(\underline h+x))\big ]-f(\underline H, \underline M)\\ &\quad \ \ \ - (1-\epsilon )\delta e^{-\delta (t-T_*)}\big [u_{c_\nu }^{\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime}(\underline h(t)+x)\big ] \\ &\quad \ \ \ - (1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})2u_{c_\nu }^{\prime}(2\underline h(t)). \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} &\underline{H}_t- d_1\underline{H}_{xx}-f(\underline H, \underline M)\\ &\quad=\delta \epsilon \big [u_{c_\nu }(\underline h(t)-x) +u_{c_\nu }(\underline h(t)+x)-u_{c_\nu }(2\underline h(t))\big ]\\ &\quad \ \ \ +(1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})\big [u_{c_\nu }^{\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime}(\underline h(t)+x)-2u_{c_\nu }^{\prime}(2\underline h(t))\big ] \\ &\quad\ \ \ -d_1(1-\epsilon )\big [u_{c_\nu }^{\prime\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime\prime}(\underline h(t)+x)\big ]-f(\underline H, \underline M)\\ &\quad= \delta \epsilon \big [u_{c_\nu }(\underline h(t)-x) +u_{c_\nu }(\underline h(t)+x)-u_{c_\nu }(2\underline h(t))\big ]\\ &\quad \ \ \ +(1-\epsilon )\big [ f(u_{c_\nu }(\underline h-x),v_{c_\nu }(\underline h-x))+f(u_{c_\nu }(\underline h+x), v_{c_\nu }(\underline h+x))\big ]-f(\underline H, \underline M)\\ &\quad \ \ \ - (1-\epsilon )\delta e^{-\delta (t-T_*)}\big [u_{c_\nu }^{\prime}(\underline h(t)-x) +u_{c_\nu }^{\prime}(\underline h(t)+x)\big ] \\ &\quad \ \ \ - (1-\epsilon )(c_\nu - \delta e^{-\delta (t-T_*)})2u_{c_\nu }^{\prime}(2\underline h(t)). \end{aligned} \end{eqnarray*}
For
![]() $t\geq T_*$
and
$t\geq T_*$
and
![]() $x\in [\!-\underline h(t), \underline h(t)]$
, by the monotonicity of
$x\in [\!-\underline h(t), \underline h(t)]$
, by the monotonicity of
![]() $u_{c_\nu }$
, we have
$u_{c_\nu }$
, we have
Since
![]() $\delta \lt c_\nu$
and
$\delta \lt c_\nu$
and
![]() $0\lt \tilde \epsilon \ll 1$
, we have
$0\lt \tilde \epsilon \ll 1$
, we have
and by (2.3),
Hence, we have, for
![]() $t\geq T_*$
and
$t\geq T_*$
and
![]() $x\in [\!-\underline h(t), \underline h(t)]$
,
$x\in [\!-\underline h(t), \underline h(t)]$
,
 \begin{equation*}\underline {H}_t- d_1\underline {H}_{xx}-f(\underline H, \underline M) \\ \leq \delta H^*\epsilon (t)+Ce^{2 \hat \mu _1 \underline h(t)} +A(x,t)+B(x,t), \end{equation*}
\begin{equation*}\underline {H}_t- d_1\underline {H}_{xx}-f(\underline H, \underline M) \\ \leq \delta H^*\epsilon (t)+Ce^{2 \hat \mu _1 \underline h(t)} +A(x,t)+B(x,t), \end{equation*}
where
and
We next choose a suitable
![]() $K_0\gt 0$
and estimate
$K_0\gt 0$
and estimate
for
![]() $x$
in the following three intervals, separately:
$x$
in the following three intervals, separately:
With
![]() $\delta _0\gt 0$
determined by Lemma 3.3, we fix
$\delta _0\gt 0$
determined by Lemma 3.3, we fix
![]() $K_0\gt 0$
so that
$K_0\gt 0$
so that
Then for
![]() $x\in I_3(t)$
,
$x\in I_3(t)$
,
![]() $t\geq T_*$
and
$t\geq T_*$
and
![]() $0\lt \tilde \epsilon \ll 1$
, clearly
$0\lt \tilde \epsilon \ll 1$
, clearly
Moreover, either
![]() $\underline h(t)-x\geq \underline h(t)$
or
$\underline h(t)-x\geq \underline h(t)$
or
![]() $\underline h(t)+x\geq \underline h(t)$
must hold, and hence
$\underline h(t)+x\geq \underline h(t)$
must hold, and hence
provided that
![]() $L$
is sufficiently large such that
$L$
is sufficiently large such that
Clearly, we also have
Thus, we can use Lemma 3.3 to obtain
where
![]() $\sigma _0\gt 0$
satisfies
$\sigma _0\gt 0$
satisfies
Since
![]() $B(x,t)\leq 0$
and
$B(x,t)\leq 0$
and
![]() $2\hat \mu _1 c_\nu \lt -\delta$
, we thus obtain, for
$2\hat \mu _1 c_\nu \lt -\delta$
, we thus obtain, for
![]() $x\in I_3(t)$
and
$x\in I_3(t)$
and
![]() $t\geq T_*\gg 1$
,
$t\geq T_*\gg 1$
,
provided that
For
![]() $x\in I_1(t)$
and
$x\in I_1(t)$
and
![]() $t\geq T_*$
, with
$t\geq T_*$
, with
![]() $0\lt \tilde \epsilon \ll 1$
, we have
$0\lt \tilde \epsilon \ll 1$
, we have
with
and
which imply
Therefore, for some
![]() $\tilde C\gt 0$
, all
$\tilde C\gt 0$
, all
![]() $x\in I_1(t)$
and
$x\in I_1(t)$
and
![]() $t\geq T_*$
, with
$t\geq T_*$
, with
![]() $0\lt \tilde \epsilon \ll 1$
, we have
$0\lt \tilde \epsilon \ll 1$
, we have
 \begin{equation*}\begin {aligned} &\delta H^*\epsilon (t)+Ce^{2 \hat \mu _1 \underline h(t)} +A(x,t)+B(x,t)\\ &\quad\leq \tilde C \left [e^{|\hat \mu _1|(1-L)}e^{\hat \mu _1 c_\nu (t-T_*)}+\tilde \epsilon e^{-\delta (t-T_*)t}\right ]-\frac {\sigma _1}2 \delta e^{-\delta (t-T_*)}\\ &\quad\leq \Big [\tilde Ce^{|\hat \mu _1|(1-L)}+\tilde C\tilde \epsilon -\frac {\sigma _1}2 \delta \Big ] e^{-\delta (t-T_*)}\lt 0 \end {aligned}\end{equation*}
\begin{equation*}\begin {aligned} &\delta H^*\epsilon (t)+Ce^{2 \hat \mu _1 \underline h(t)} +A(x,t)+B(x,t)\\ &\quad\leq \tilde C \left [e^{|\hat \mu _1|(1-L)}e^{\hat \mu _1 c_\nu (t-T_*)}+\tilde \epsilon e^{-\delta (t-T_*)t}\right ]-\frac {\sigma _1}2 \delta e^{-\delta (t-T_*)}\\ &\quad\leq \Big [\tilde Ce^{|\hat \mu _1|(1-L)}+\tilde C\tilde \epsilon -\frac {\sigma _1}2 \delta \Big ] e^{-\delta (t-T_*)}\lt 0 \end {aligned}\end{equation*}
provided that
By the symmetry of
![]() $A(x,t)$
and
$A(x,t)$
and
![]() $B(x,t)$
in
$B(x,t)$
in
![]() $x$
, we see that the above also hold for
$x$
, we see that the above also hold for
![]() $x\in I_2(t)$
.
$x\in I_2(t)$
.
Let us note that, if we refine our choice of
![]() $\delta$
to
$\delta$
to
then it is possible to take
![]() $L$
sufficiently large and
$L$
sufficiently large and
![]() $\tilde \epsilon \gt 0$
sufficiently small such that all the inequalities in (3.23), (3.22), (3.24) and (3.25) hold. Thus, for such
$\tilde \epsilon \gt 0$
sufficiently small such that all the inequalities in (3.23), (3.22), (3.24) and (3.25) hold. Thus, for such
![]() $\tilde \epsilon$
and
$\tilde \epsilon$
and
![]() $L$
, (3.17) holds.
$L$
, (3.17) holds.
Moreover, by similar arguments we see that
![]() $\tilde \epsilon$
and
$\tilde \epsilon$
and
![]() $L$
can be chosen so that (3.18) holds simultaneously. Note that the value
$L$
can be chosen so that (3.18) holds simultaneously. Note that the value
![]() $T_*=T_*(L, \tilde \epsilon )$
is finalised only after the choice of
$T_*=T_*(L, \tilde \epsilon )$
is finalised only after the choice of
![]() $L$
and
$L$
and
![]() $\tilde \epsilon$
have been made.
$\tilde \epsilon$
have been made.
Proof of Proposition 3.1. It follows from Lemmas 3.2 and 3.4 that
for
![]() $t\gt T=\!:\,\max \{T_\ast,T^\ast \}$
. Hence, there exists
$t\gt T=\!:\,\max \{T_\ast,T^\ast \}$
. Hence, there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
This implies, by considering the solution of (1.3) with initial function
![]() $(H_0(\!-x), M_0(\!-x))$
, that
$(H_0(\!-x), M_0(\!-x))$
, that
![]() $|g(t)+c_\nu t|\lt C\mbox{ for all } t\gt 0$
. The proof of Proposition 3.1 is now complete.
$|g(t)+c_\nu t|\lt C\mbox{ for all } t\gt 0$
. The proof of Proposition 3.1 is now complete.
4. Convergence
In this section, we prove Theorem 1.2. The crucial step is to show that
![]() $h(t)-c_\nu t\to h^\ast$
as
$h(t)-c_\nu t\to h^\ast$
as
![]() $t\rightarrow \infty$
.
$t\rightarrow \infty$
.
According to Proposition 3.1, there exists
![]() $C\gt 0$
such that
$C\gt 0$
such that
We now set
and denote
Obviously,
Moreover,
and
![]() $(\phi,\psi,l)$
satisfies
$(\phi,\psi,l)$
satisfies
 \begin{eqnarray*} \begin{cases} \phi _t=d_1 \phi _{xx}+c_\nu \phi _x+a_1(e_1-\phi )\psi -b_1\phi,&-k(t)\lt x\lt l(t),\quad t\gt 0,\\ \psi _t=d_2 \psi _{xx}+c_\nu \psi _x+a_2(e_2-\psi )\phi -b_2 \psi,&-k(t)\lt x\lt l(t),\quad t\gt 0,\\ \phi (l(t),t)=\psi (l(t),t)=0,&t\gt 0,\\ l^{\prime}(t)=-\nu \phi _{x}(l(t),t)-c_\nu,& t\gt 0. \end{cases} \end{eqnarray*}
\begin{eqnarray*} \begin{cases} \phi _t=d_1 \phi _{xx}+c_\nu \phi _x+a_1(e_1-\phi )\psi -b_1\phi,&-k(t)\lt x\lt l(t),\quad t\gt 0,\\ \psi _t=d_2 \psi _{xx}+c_\nu \psi _x+a_2(e_2-\psi )\phi -b_2 \psi,&-k(t)\lt x\lt l(t),\quad t\gt 0,\\ \phi (l(t),t)=\psi (l(t),t)=0,&t\gt 0,\\ l^{\prime}(t)=-\nu \phi _{x}(l(t),t)-c_\nu,& t\gt 0. \end{cases} \end{eqnarray*}
4.1. Limit along a sequence
 $\boldsymbol{t}_\boldsymbol{n}\rightarrow \infty$
$\boldsymbol{t}_\boldsymbol{n}\rightarrow \infty$
Let
![]() $\{t_n\}$
be a sequence satisfying
$\{t_n\}$
be a sequence satisfying
![]() $t_n\gt 0$
,
$t_n\gt 0$
,
![]() $t_n\rightarrow \infty$
and
$t_n\rightarrow \infty$
and
![]() $l(t_n)\to \liminf _{t\to +\infty }l(t)$
as
$l(t_n)\to \liminf _{t\to +\infty }l(t)$
as
![]() $n\rightarrow \infty$
. Define
$n\rightarrow \infty$
. Define
Lemma 4.1.
Subject to a subsequence, as
![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
where
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $\Omega \,:\!=\{(x,t):-\infty \lt x\lt L(t),t\in \mathbb{R}\}$
and
$\Omega \,:\!=\{(x,t):-\infty \lt x\lt L(t),t\in \mathbb{R}\}$
and
![]() $C_{loc}^{1+\alpha,\frac{1+\alpha }{2}}(\Omega )$
denotes the space of functions
$C_{loc}^{1+\alpha,\frac{1+\alpha }{2}}(\Omega )$
denotes the space of functions
![]() $\phi (x,t)$
which have bounded
$\phi (x,t)$
which have bounded
![]() $(1+\alpha )$
-Hölder norm in
$(1+\alpha )$
-Hölder norm in
![]() $x$
and bounded
$x$
and bounded
![]() $\frac{1+\alpha }{2}$
-Hölder norm in
$\frac{1+\alpha }{2}$
-Hölder norm in
![]() $t$
over any compact subset of
$t$
over any compact subset of
![]() $\Omega$
. Moreover,
$\Omega$
. Moreover,
![]() $(\Phi (x,t),\Psi (x,t),L(t))$
satisfies
$(\Phi (x,t),\Psi (x,t),L(t))$
satisfies
 \begin{eqnarray} \begin{cases} \Phi _t=d_1 \Phi _{xx}+c_\nu \Phi _x+a_1(e_1-\Phi )\Psi -b_1\Phi,&(x,t)\in \Omega,\\ \Psi _t=d_2 \Psi _{xx}+c_\nu \Psi _x+a_2(e_2-\Psi )\Phi -b_2\Psi,&(x,t)\in \Omega,\\ \Phi (L(t),t)=\Psi (L(t),t)=0,&t\in \mathbb{R},\\ L^{\prime}(t)=-\nu \Phi _{x}(L(t),t)-c_\nu,\ L(t)\geq L(0),& t\in \mathbb{R}. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \Phi _t=d_1 \Phi _{xx}+c_\nu \Phi _x+a_1(e_1-\Phi )\Psi -b_1\Phi,&(x,t)\in \Omega,\\ \Psi _t=d_2 \Psi _{xx}+c_\nu \Psi _x+a_2(e_2-\Psi )\Phi -b_2\Psi,&(x,t)\in \Omega,\\ \Phi (L(t),t)=\Psi (L(t),t)=0,&t\in \mathbb{R},\\ L^{\prime}(t)=-\nu \Phi _{x}(L(t),t)-c_\nu,\ L(t)\geq L(0),& t\in \mathbb{R}. \end{cases} \end{eqnarray}
Proof. It follows from Lemma 2.4 that there exists
![]() $C_0\gt 0$
such that
$C_0\gt 0$
such that
![]() $0\lt h^{\prime}(t)\leq C_0$
for
$0\lt h^{\prime}(t)\leq C_0$
for
![]() $t\gt 0$
, which leads to
$t\gt 0$
, which leads to
Denote
Then
![]() $(\tilde{\phi }_n(\xi,t),\tilde{\psi }_n(\xi,t),l_n(t))$
satisfies
$(\tilde{\phi }_n(\xi,t),\tilde{\psi }_n(\xi,t),l_n(t))$
satisfies
 \begin{eqnarray} \begin{cases} \tilde{\phi }_{nt}=\dfrac{d_1}{l_n^2(t)} \tilde{\phi }_{n\xi \xi }+\dfrac{\xi l_n^{\prime}(t)+c_\nu }{l_n(t)} \tilde{\phi }_{n\xi }+a_1(e_1-\tilde{\phi }_n)\tilde{\psi }_n-b_1\tilde{\phi }_n,\\ \tilde{\psi }_{nt}=\dfrac{d_2}{l_n^2(t)} \tilde{\psi }_{n\xi \xi }+\dfrac{\xi l_n^{\prime}(t)+c_\nu }{l_n(t)} \tilde{\psi }_{n\xi }+a_2(e_2-\tilde{\psi }_n)\tilde{\phi }_n-b_2\tilde{\psi }_n \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \tilde{\phi }_{nt}=\dfrac{d_1}{l_n^2(t)} \tilde{\phi }_{n\xi \xi }+\dfrac{\xi l_n^{\prime}(t)+c_\nu }{l_n(t)} \tilde{\phi }_{n\xi }+a_1(e_1-\tilde{\phi }_n)\tilde{\psi }_n-b_1\tilde{\phi }_n,\\ \tilde{\psi }_{nt}=\dfrac{d_2}{l_n^2(t)} \tilde{\psi }_{n\xi \xi }+\dfrac{\xi l_n^{\prime}(t)+c_\nu }{l_n(t)} \tilde{\psi }_{n\xi }+a_2(e_2-\tilde{\psi }_n)\tilde{\phi }_n-b_2\tilde{\psi }_n \end{cases} \end{eqnarray}
for
![]() $-k_n(t)/l_n(t)\lt \xi \lt 1$
,
$-k_n(t)/l_n(t)\lt \xi \lt 1$
,
![]() $t\gt -t_n$
, and
$t\gt -t_n$
, and
 \begin{eqnarray} \begin{cases} \tilde{\phi }_n(1,t)=\tilde{\psi }_n(1,t)=0,\ t\gt -t_n,\\ l_n^{\prime}(t)=-\dfrac{\nu }{l_n(t)} \tilde{\phi }_{n\xi }(1,t)-c_\nu,\ t\gt -t_n. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \tilde{\phi }_n(1,t)=\tilde{\psi }_n(1,t)=0,\ t\gt -t_n,\\ l_n^{\prime}(t)=-\dfrac{\nu }{l_n(t)} \tilde{\phi }_{n\xi }(1,t)-c_\nu,\ t\gt -t_n. \end{cases} \end{eqnarray}
Owing to Lemma 2.4,
![]() $(H,M)(x,t)$
is uniformly bounded for
$(H,M)(x,t)$
is uniformly bounded for
![]() $x\in [g(t),h(t)]$
and
$x\in [g(t),h(t)]$
and
![]() $t\in (0,\infty )$
, which implies that
$t\in (0,\infty )$
, which implies that
![]() $(\phi _n,\psi _n)$
is uniformly bounded in
$(\phi _n,\psi _n)$
is uniformly bounded in
![]() $\{(x,t):-k_n(t)\lt x\lt l_n(t),t\geq -t_n\}$
. Hence, in view of (4.1), for any given
$\{(x,t):-k_n(t)\lt x\lt l_n(t),t\geq -t_n\}$
. Hence, in view of (4.1), for any given
![]() $R\gt 0$
and
$R\gt 0$
and
![]() $T\in \mathbb{R}$
, using the interior-boundary
$T\in \mathbb{R}$
, using the interior-boundary
![]() $L^p$
estimates to (4.3) and (4.4) over
$L^p$
estimates to (4.3) and (4.4) over
![]() $[\!-R-2,1]\times [T-2,T+1]$
, for any
$[\!-R-2,1]\times [T-2,T+1]$
, for any
![]() $p\gt 1$
we have
$p\gt 1$
we have
where
![]() $C_R$
is a constant depending on
$C_R$
is a constant depending on
![]() $R$
and
$R$
and
![]() $p$
but independent of
$p$
but independent of
![]() $n$
and
$n$
and
![]() $T$
. Furthermore, for any
$T$
. Furthermore, for any
![]() $\alpha ^{\prime}\in (0,1)$
, we can take
$\alpha ^{\prime}\in (0,1)$
, we can take
![]() $p\gt 1$
large enough and use the Sobolev embedding theorem to obtain
$p\gt 1$
large enough and use the Sobolev embedding theorem to obtain
where
![]() $\tilde{C}_R$
is a constant depending on
$\tilde{C}_R$
is a constant depending on
![]() $R$
and
$R$
and
![]() $\alpha ^{\prime}$
but independent of
$\alpha ^{\prime}$
but independent of
![]() $n$
and
$n$
and
![]() $T$
. From (4.4) and (4.5), we conclude
$T$
. From (4.4) and (4.5), we conclude
where
![]() $\tilde{C}_1$
is a constant depending on
$\tilde{C}_1$
is a constant depending on
![]() $R$
and
$R$
and
![]() $\alpha ^{\prime}$
but independent of
$\alpha ^{\prime}$
but independent of
![]() $n$
and
$n$
and
![]() $T$
too. Hence by passing to a subsequence, still denoted by itself, we have, for some
$T$
too. Hence by passing to a subsequence, still denoted by itself, we have, for some
![]() $\alpha \in (0,\alpha ^{\prime})$
,
$\alpha \in (0,\alpha ^{\prime})$
,
Now, applying standard regularity theory to (4.3)–(4.4), we see that
![]() $(\tilde{\Phi },\tilde{\Psi },L)$
satisfies the following equations in the classical sense:
$(\tilde{\Phi },\tilde{\Psi },L)$
satisfies the following equations in the classical sense:
 \begin{eqnarray*} \begin{cases} \tilde{\Phi }_{t}=\dfrac{d_1}{L^2(t)} \tilde{\Phi }_{\xi \xi }+\dfrac{\xi L^{\prime}(t)+c_\nu }{L(t)} \tilde{\Phi }_{\xi }+a_1(e_1-\tilde{\Phi })\tilde{\Psi }-b_1\tilde{\Phi },&\xi \in (\!-\infty,1],\ t\in \mathbb{R},\\ \tilde{\Psi }_{t}=\dfrac{d_2}{L^2(t)} \tilde{\Psi }_{\xi \xi }+\dfrac{\xi L^{\prime}(t)+c_\nu }{L(t)} \tilde{\Psi }_{\xi }+a_2(e_2-\tilde{\Psi })\tilde{\Phi }-b_2\tilde{\Psi },&\xi \in (\!-\infty,1],\ t\in \mathbb{R},\\ \tilde{\Phi }(1,t)=\tilde{\Psi }(1,t)=0,&t\in \mathbb{R},\\ L^{\prime}(t)=-\dfrac{\nu }{L(t)} \tilde{\Phi }_{\xi }(1,t)-c_\nu,& t\in \mathbb{R}. \end{cases} \end{eqnarray*}
\begin{eqnarray*} \begin{cases} \tilde{\Phi }_{t}=\dfrac{d_1}{L^2(t)} \tilde{\Phi }_{\xi \xi }+\dfrac{\xi L^{\prime}(t)+c_\nu }{L(t)} \tilde{\Phi }_{\xi }+a_1(e_1-\tilde{\Phi })\tilde{\Psi }-b_1\tilde{\Phi },&\xi \in (\!-\infty,1],\ t\in \mathbb{R},\\ \tilde{\Psi }_{t}=\dfrac{d_2}{L^2(t)} \tilde{\Psi }_{\xi \xi }+\dfrac{\xi L^{\prime}(t)+c_\nu }{L(t)} \tilde{\Psi }_{\xi }+a_2(e_2-\tilde{\Psi })\tilde{\Phi }-b_2\tilde{\Psi },&\xi \in (\!-\infty,1],\ t\in \mathbb{R},\\ \tilde{\Phi }(1,t)=\tilde{\Psi }(1,t)=0,&t\in \mathbb{R},\\ L^{\prime}(t)=-\dfrac{\nu }{L(t)} \tilde{\Phi }_{\xi }(1,t)-c_\nu,& t\in \mathbb{R}. \end{cases} \end{eqnarray*}
By setting
![]() $(\Phi,\Psi )(x,t)=(\tilde{\Phi },\tilde{\Psi })(x/L(t),t)$
, it is easy to verify that
$(\Phi,\Psi )(x,t)=(\tilde{\Phi },\tilde{\Psi })(x/L(t),t)$
, it is easy to verify that
![]() $(\Phi,\Psi,L)$
satisfies (4.2) and
$(\Phi,\Psi,L)$
satisfies (4.2) and
Finally, since
![]() $L(0)=\lim _{n\to \infty }l(t_n)=\liminf _{t\to \infty }l(t)$
and
$L(0)=\lim _{n\to \infty }l(t_n)=\liminf _{t\to \infty }l(t)$
and
![]() $L(t)=\lim _{n\to \infty }l(t_n+t)$
, clearly
$L(t)=\lim _{n\to \infty }l(t_n+t)$
, clearly
![]() $L(t)\geq L(0)$
for any
$L(t)\geq L(0)$
for any
![]() $t\in \mathbb R$
. This completes the proof.
$t\in \mathbb R$
. This completes the proof.
4.2. Determine the limit pair
 $(\Phi,\Psi,\boldsymbol{L})$
$(\Phi,\Psi,\boldsymbol{L})$
We show that
Due to (4.1), we have
It follows from Lemma 3.4 that, for
![]() $x\in [\!-\underline h(t+t_n)-k(t+t_n), \underline h(t+t_n)-k(t+t_n)]$
and
$x\in [\!-\underline h(t+t_n)-k(t+t_n), \underline h(t+t_n)-k(t+t_n)]$
and
![]() $t+t_n\geq T_*$
,
$t+t_n\geq T_*$
,
 \begin{eqnarray} \begin{cases} \phi _n(x,t)\geq (1-\tilde \epsilon \,e^{-\delta (t+t_n-T_*)})\hat \phi _n(x,t),\\ \psi _n(x,t)\geq (1-\tilde \epsilon \, e^{-\delta (t+t_n-T_*)})\hat \psi _n(x,t), \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \phi _n(x,t)\geq (1-\tilde \epsilon \,e^{-\delta (t+t_n-T_*)})\hat \phi _n(x,t),\\ \psi _n(x,t)\geq (1-\tilde \epsilon \, e^{-\delta (t+t_n-T_*)})\hat \psi _n(x,t), \end{cases} \end{eqnarray}
where
 \begin{align*} \begin{cases} \hat \phi _n(x,t)\,:\!=u_{c_\nu }(\underline{h}(t+t_n)-k(t+t_n)-x)+u_{c_\nu }(\underline{h}(t+t_n)+k(t+t_n)+x)-u_{c_\nu }(2\underline{h}(t+t_n)),\\ \hat \psi _n(x,t)\,:\!=v_{c_\nu }(\underline{h}(t+t_n)-k(t+t_n)-x)+v_{c_\nu }(\underline{h}(t+t_n)+k(t+t_n)+x)-v_{c_\nu }(2\underline{h}(t+t_n)). \end{cases} \end{align*}
\begin{align*} \begin{cases} \hat \phi _n(x,t)\,:\!=u_{c_\nu }(\underline{h}(t+t_n)-k(t+t_n)-x)+u_{c_\nu }(\underline{h}(t+t_n)+k(t+t_n)+x)-u_{c_\nu }(2\underline{h}(t+t_n)),\\ \hat \psi _n(x,t)\,:\!=v_{c_\nu }(\underline{h}(t+t_n)-k(t+t_n)-x)+v_{c_\nu }(\underline{h}(t+t_n)+k(t+t_n)+x)-v_{c_\nu }(2\underline{h}(t+t_n)). \end{cases} \end{align*}
It is easily seen that there exists
![]() $C_0\in \mathbb R$
such that
$C_0\in \mathbb R$
such that
![]() $\underline{h}(t+t_n)-k(t+t_n)\geq C_0$
for
$\underline{h}(t+t_n)-k(t+t_n)\geq C_0$
for
![]() $t+t_n\geq T_*$
. Moreover,
$t+t_n\geq T_*$
. Moreover,
It follows that, for
![]() $x\leq C_0\leq L(t)$
and
$x\leq C_0\leq L(t)$
and
![]() $t\in \mathbb R$
,
$t\in \mathbb R$
,
Hence, letting
![]() $n\rightarrow \infty$
in (4.6) we obtain
$n\rightarrow \infty$
in (4.6) we obtain
Now we define
Thanks to (4.7) and
![]() $(\Phi,\Psi )(L(t),t)=(0, 0)$
with
$(\Phi,\Psi )(L(t),t)=(0, 0)$
with
![]() $L(t)\in [C, 3C]$
, we see that
$L(t)\in [C, 3C]$
, we see that
![]() $R^\ast$
is finite. Moreover,
$R^\ast$
is finite. Moreover,
and
Lemma 4.2.
![]() $R^\ast =L(0)$
.
$R^\ast =L(0)$
.
Proof. On the contrary, suppose
![]() $R^\ast \lt L(0)=\min _{t\in \mathbb{R}}L(t)$
.
$R^\ast \lt L(0)=\min _{t\in \mathbb{R}}L(t)$
.
Step 1. We show that
Otherwise, there exists
![]() $(x_0,t_0)\in (\!-\infty, R^*)\times \mathbb R$
such that
$(x_0,t_0)\in (\!-\infty, R^*)\times \mathbb R$
such that
Observe that
![]() $\left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x)$
satisfies the first two equations in (4.2) for
$\left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x)$
satisfies the first two equations in (4.2) for
![]() $(x,t)\in (\!-\infty, R^*)\times \mathbb R$
, and we already know
$(x,t)\in (\!-\infty, R^*)\times \mathbb R$
, and we already know
![]() $(\Phi,\Psi )(x,t)\succeq \left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x)$
for such
$(\Phi,\Psi )(x,t)\succeq \left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x)$
for such
![]() $(x,t)$
. Without loss of generality, we assume
$(x,t)$
. Without loss of generality, we assume
![]() $\Phi (x_0,t_0)=u_{c_\nu }(R^\ast -x_0)$
. Set
$\Phi (x_0,t_0)=u_{c_\nu }(R^\ast -x_0)$
. Set
![]() $\varpi (x,t)=u_{c_\nu }(R^\ast -x)-\Phi (x,t)$
and take
$\varpi (x,t)=u_{c_\nu }(R^\ast -x)-\Phi (x,t)$
and take
![]() $\overline{K}\geq a_1M^\ast$
. Then,
$\overline{K}\geq a_1M^\ast$
. Then,
![]() $\varpi (x,t)\leq 0$
in
$\varpi (x,t)\leq 0$
in
![]() $(\!-\infty, R^*)\times \mathbb R$
and
$(\!-\infty, R^*)\times \mathbb R$
and
 \begin{eqnarray*} \begin{aligned} &\varpi _t-d_1\varpi _{xx}-c_\nu \varpi +(b_1+\overline{K})\varpi \\ &\quad=\ a_1(e_1-u_{c_\nu }(R^\ast -x))v_{c_\nu }(R^\ast -x)-a_1(e_1-\Phi )\Psi +\overline{K}\varpi \\ &\quad\leq \ a_1(e_1-u_{c_\nu }(R^\ast -x))v_{c_\nu }(R^\ast -x)-a_1(e_1-\Phi )v_{c_\nu }(R^\ast -x)+\overline{K}\varpi \\ &\quad=-a_1\varpi v_{c_\nu }(R^\ast -x)+\overline{K}\varpi \leq 0. \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} &\varpi _t-d_1\varpi _{xx}-c_\nu \varpi +(b_1+\overline{K})\varpi \\ &\quad=\ a_1(e_1-u_{c_\nu }(R^\ast -x))v_{c_\nu }(R^\ast -x)-a_1(e_1-\Phi )\Psi +\overline{K}\varpi \\ &\quad\leq \ a_1(e_1-u_{c_\nu }(R^\ast -x))v_{c_\nu }(R^\ast -x)-a_1(e_1-\Phi )v_{c_\nu }(R^\ast -x)+\overline{K}\varpi \\ &\quad=-a_1\varpi v_{c_\nu }(R^\ast -x)+\overline{K}\varpi \leq 0. \end{aligned} \end{eqnarray*}
Since
![]() $\varpi (x_0,t_0)=0$
, the strong maximum principle implies that
$\varpi (x_0,t_0)=0$
, the strong maximum principle implies that
![]() $\varpi (x,t)\equiv 0$
for
$\varpi (x,t)\equiv 0$
for
![]() $(x,t)\in (\!-\infty, R^*)\times \mathbb R$
. But this is impossible since
$(x,t)\in (\!-\infty, R^*)\times \mathbb R$
. But this is impossible since
Thus, (4.8) holds.
Step 2. We prove that, for any
![]() $x\leq R^*$
,
$x\leq R^*$
,
 \begin{eqnarray} \begin{cases} \omega _1(x)=\sup _{y\in [x, R^*], t\in \mathbb{R}}[u_{c_\nu }(R^\ast -y)-\Phi (y,t)]\lt 0,\\ \omega _2(x)=\sup _{y\in [x, R^*], t\in \mathbb{R}}[v_{c_\nu }(R^\ast -y)-\Psi (y,t)]\lt 0. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \omega _1(x)=\sup _{y\in [x, R^*], t\in \mathbb{R}}[u_{c_\nu }(R^\ast -y)-\Phi (y,t)]\lt 0,\\ \omega _2(x)=\sup _{y\in [x, R^*], t\in \mathbb{R}}[v_{c_\nu }(R^\ast -y)-\Psi (y,t)]\lt 0. \end{cases} \end{eqnarray}
Obviously,
![]() $\omega _i(x)\leq 0$
for
$\omega _i(x)\leq 0$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $x\leq R^*$
. If (4.9) does not hold, then there exists
$x\leq R^*$
. If (4.9) does not hold, then there exists
![]() $x_0\in (\!-\infty,R^\ast )$
such that
$x_0\in (\!-\infty,R^\ast )$
such that
As a consequence of Step 1, we see that in (4.9),
![]() $\omega _i(x_0)$
is not achieved by any
$\omega _i(x_0)$
is not achieved by any
![]() $(y,t)\in [x_0, R^*]\times \mathbb R$
. Therefore, there exists a sequence
$(y,t)\in [x_0, R^*]\times \mathbb R$
. Therefore, there exists a sequence
![]() $\{(y_n,s_n)\}\subset [x_0, R^*]\times \mathbb{R}$
with
$\{(y_n,s_n)\}\subset [x_0, R^*]\times \mathbb{R}$
with
![]() $|s_n|\rightarrow \infty$
such that
$|s_n|\rightarrow \infty$
such that
By passing to a subsequence, we may assume that
![]() $\lim _{n\to \infty }y_n=y_0\in [x_0, R^*]$
. Set
$\lim _{n\to \infty }y_n=y_0\in [x_0, R^*]$
. Set
Then repeating the same argument used in the proof of Lemma 4.1 and passing to a subsequence if necessary, we may assume that, for
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
with
![]() $\widetilde{\Omega }=\{(t,x):x\lt \tilde L(t),\ t\in \mathbb R\}$
, and
$\widetilde{\Omega }=\{(t,x):x\lt \tilde L(t),\ t\in \mathbb R\}$
, and
![]() $\left(\widetilde{\Phi },\widetilde{\Psi },\widetilde{L}\right)$
satisfies
$\left(\widetilde{\Phi },\widetilde{\Psi },\widetilde{L}\right)$
satisfies
 \begin{eqnarray} \begin{cases} \widetilde{\Phi }_t=d_1 \widetilde{\Phi }_{xx}+c_\nu \widetilde{\Phi }_x+a_1(e_1-\widetilde{\Phi })\widetilde{\Psi }-b_1\widetilde{\Phi },&-\infty \lt x\lt \widetilde{L}(t),\ t\in \mathbb{R},\\ \widetilde{\Psi }_t=d_2 \widetilde{\Psi }_{xx}+c_\nu \widetilde{\Psi }_x+a_2(e_2-\widetilde{\Psi })\widetilde{\Phi }-b_2\widetilde{\Psi },&-\infty \lt x\lt \widetilde{L}(t),\ t\in \mathbb{R},\\ \widetilde{\Phi }(\widetilde{L}(t),t)=\widetilde{\Psi }(\widetilde{L}(t),t)=0,&t\in \mathbb{R}. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \widetilde{\Phi }_t=d_1 \widetilde{\Phi }_{xx}+c_\nu \widetilde{\Phi }_x+a_1(e_1-\widetilde{\Phi })\widetilde{\Psi }-b_1\widetilde{\Phi },&-\infty \lt x\lt \widetilde{L}(t),\ t\in \mathbb{R},\\ \widetilde{\Psi }_t=d_2 \widetilde{\Psi }_{xx}+c_\nu \widetilde{\Psi }_x+a_2(e_2-\widetilde{\Psi })\widetilde{\Phi }-b_2\widetilde{\Psi },&-\infty \lt x\lt \widetilde{L}(t),\ t\in \mathbb{R},\\ \widetilde{\Phi }(\widetilde{L}(t),t)=\widetilde{\Psi }(\widetilde{L}(t),t)=0,&t\in \mathbb{R}. \end{cases} \end{eqnarray}
Moreover, for
![]() $-\infty \lt x\lt R^*-y_0,\ t\in \mathbb{R}$
,
$-\infty \lt x\lt R^*-y_0,\ t\in \mathbb{R}$
,
and
Since
![]() $(u_{c_\nu },v_{c_\nu })(R^\ast -y_0-x)$
satisfies (4.10) with
$(u_{c_\nu },v_{c_\nu })(R^\ast -y_0-x)$
satisfies (4.10) with
![]() $\widetilde{L}$
replaced by
$\widetilde{L}$
replaced by
![]() $R^\ast -y_0$
and (4.10) is a cooperative system, repeating the same argument as in Step 1 and applying the strong maximum principle we can conclude that
$R^\ast -y_0$
and (4.10) is a cooperative system, repeating the same argument as in Step 1 and applying the strong maximum principle we can conclude that
![]() $\widetilde{\Phi }(x,t)\equiv u_{c_\nu }(R^\ast -y_0-x)$
or
$\widetilde{\Phi }(x,t)\equiv u_{c_\nu }(R^\ast -y_0-x)$
or
![]() $\widetilde{\Psi }(x,t)\equiv v_{c_\nu }(R^\ast -y_0-x)$
for
$\widetilde{\Psi }(x,t)\equiv v_{c_\nu }(R^\ast -y_0-x)$
for
![]() $x\lt R^*-y_0$
with
$x\lt R^*-y_0$
with
![]() $t\leq 0$
. It follows that
$t\leq 0$
. It follows that
![]() $\widetilde{\Phi }(R^*-y_0,0)=0$
or
$\widetilde{\Phi }(R^*-y_0,0)=0$
or
![]() $\widetilde{\Psi }(R^*-y_0,0)=0$
, which is impossible since
$\widetilde{\Psi }(R^*-y_0,0)=0$
, which is impossible since
![]() $\tilde L(0)\gt R^*-y_0$
.
$\tilde L(0)\gt R^*-y_0$
.
Step 3. Completion of the proof.
In view of
![]() $(u_{c_\nu },v_{c_\nu })(R^\ast -x)\rightarrow (H^\ast,M^\ast )$
as
$(u_{c_\nu },v_{c_\nu })(R^\ast -x)\rightarrow (H^\ast,M^\ast )$
as
![]() $x\rightarrow -\infty$
, for any small
$x\rightarrow -\infty$
, for any small
![]() $\epsilon _0\gt 0$
we can find
$\epsilon _0\gt 0$
we can find
![]() $R_0=R_0(\epsilon _0)\lt R^*$
large negative such that
$R_0=R_0(\epsilon _0)\lt R^*$
large negative such that
Then choose
![]() $\epsilon \in (0,\epsilon _0)$
such that
$\epsilon \in (0,\epsilon _0)$
such that
where
![]() $\omega _i,i=1,2$
are defined in (4.9).
$\omega _i,i=1,2$
are defined in (4.9).
Consider an auxiliary problem:
 \begin{eqnarray} \begin{cases} \overline{\Phi }_t=d_1 \overline{\Phi }_{xx}+c_\nu \overline{\Phi }_x+a_1(e_1-\overline{\Phi })\overline{\Psi }-b_1\overline{\Phi },&x\lt R_0,t\gt 0,\\ \overline{\Psi }_t=d_2 \overline{\Psi }_{xx}+c_\nu \overline{\Psi }_x+a_2(e_2-\overline{\Psi })\overline{\Phi }-b_2\overline{\Psi },&x\lt R_0,t\gt 0,\\ \left(\overline{\Phi },\overline{\Psi }\right)(R_0,t)=(u_{c_\nu },v_{c_\nu })(R^\ast -R_0+\epsilon ),&t\gt 0,\\ \left(\overline{\Phi },\overline{\Psi }\right)(x,0)=\left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x),&x\lt R_0. \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} \overline{\Phi }_t=d_1 \overline{\Phi }_{xx}+c_\nu \overline{\Phi }_x+a_1(e_1-\overline{\Phi })\overline{\Psi }-b_1\overline{\Phi },&x\lt R_0,t\gt 0,\\ \overline{\Psi }_t=d_2 \overline{\Psi }_{xx}+c_\nu \overline{\Psi }_x+a_2(e_2-\overline{\Psi })\overline{\Phi }-b_2\overline{\Psi },&x\lt R_0,t\gt 0,\\ \left(\overline{\Phi },\overline{\Psi }\right)(R_0,t)=(u_{c_\nu },v_{c_\nu })(R^\ast -R_0+\epsilon ),&t\gt 0,\\ \left(\overline{\Phi },\overline{\Psi }\right)(x,0)=\left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x),&x\lt R_0. \end{cases} \end{eqnarray}
Obviously,
![]() $(H^\ast,M^\ast )$
and
$(H^\ast,M^\ast )$
and
![]() $(u_{c_\nu },v_{c_\nu })(R^\ast -x)$
are a pair of upper and lower solutions of (4.11). It follows from the comparison principle that
$(u_{c_\nu },v_{c_\nu })(R^\ast -x)$
are a pair of upper and lower solutions of (4.11). It follows from the comparison principle that
for all
![]() $x\lt R_0$
and
$x\lt R_0$
and
![]() $t\gt 0$
. Moreover,
$t\gt 0$
. Moreover,
![]() $\left(\overline{\Phi },\overline{\Psi }\right)(x,t)$
is non-decreasing in
$\left(\overline{\Phi },\overline{\Psi }\right)(x,t)$
is non-decreasing in
![]() $t$
and
$t$
and
where
![]() $(\Phi ^\ast,\Psi ^\ast )$
satisfies
$(\Phi ^\ast,\Psi ^\ast )$
satisfies
 \begin{eqnarray} \begin{cases} d_1 \Phi _{xx}^\ast +c_\nu \Phi _x^\ast +a_1(e_1-\Phi ^\ast )\Psi ^\ast -b_1\Phi ^\ast =0,&-\infty \lt x\lt R_0,\\ d_2 \Psi _{xx}^\ast +c_\nu \Psi _x^\ast +a_2(e_2-\Psi ^\ast )\Phi ^\ast -b_2\Psi ^\ast =0,&-\infty \lt x\lt R_0,\\ (\Phi ^\ast,\Psi ^\ast )(\!-\infty )=(H^\ast,M^\ast ),&\\ (\Phi ^\ast,\Psi ^\ast )(R_0)=(u_{c_\nu },v_{c_\nu })(R^\ast -R_0+\epsilon ). \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} d_1 \Phi _{xx}^\ast +c_\nu \Phi _x^\ast +a_1(e_1-\Phi ^\ast )\Psi ^\ast -b_1\Phi ^\ast =0,&-\infty \lt x\lt R_0,\\ d_2 \Psi _{xx}^\ast +c_\nu \Psi _x^\ast +a_2(e_2-\Psi ^\ast )\Phi ^\ast -b_2\Psi ^\ast =0,&-\infty \lt x\lt R_0,\\ (\Phi ^\ast,\Psi ^\ast )(\!-\infty )=(H^\ast,M^\ast ),&\\ (\Phi ^\ast,\Psi ^\ast )(R_0)=(u_{c_\nu },v_{c_\nu })(R^\ast -R_0+\epsilon ). \end{cases} \end{eqnarray}
Clearly,
also satisfies (4.13), and due to
![]() $(u_{c_\nu },v_{c_\nu })(R^\ast -x+\epsilon )\succeq (u_{c_\nu },v_{c_\nu })(R^\ast -x)$
, we can apply the comparison principle to (4.11) to deduce
$(u_{c_\nu },v_{c_\nu })(R^\ast -x+\epsilon )\succeq (u_{c_\nu },v_{c_\nu })(R^\ast -x)$
, we can apply the comparison principle to (4.11) to deduce
Letting
![]() $t\to \infty$
, we obtain
$t\to \infty$
, we obtain
Let us also note that from (4.12), we have
In what follows, we prove that
To this end, let us denote
Then,
![]() $\left(\widehat{\Phi },\widehat{\Psi }\right)$
satisfies
$\left(\widehat{\Phi },\widehat{\Psi }\right)$
satisfies
 \begin{eqnarray} \begin{cases} d_1 \widehat{\Phi }_{xx}+c_\nu \widehat{\Phi }_x=(b_1+a_1\Psi ^\ast )\widehat{\Phi }-a_1(e_1-\hat{u}_{c_\nu })\widehat{\Psi },&-\infty \lt x\lt R_0,\\ d_2 \widehat{\Psi }_{xx}+c_\nu \widehat{\Psi }_x=(b_2+a_2\Phi ^\ast )\widehat{\Psi }-a_2(e_2-\hat{v}_{c_\nu })\widehat{\Phi },&-\infty \lt x\lt R_0 \end{cases} \end{eqnarray}
\begin{eqnarray} \begin{cases} d_1 \widehat{\Phi }_{xx}+c_\nu \widehat{\Phi }_x=(b_1+a_1\Psi ^\ast )\widehat{\Phi }-a_1(e_1-\hat{u}_{c_\nu })\widehat{\Psi },&-\infty \lt x\lt R_0,\\ d_2 \widehat{\Psi }_{xx}+c_\nu \widehat{\Psi }_x=(b_2+a_2\Phi ^\ast )\widehat{\Psi }-a_2(e_2-\hat{v}_{c_\nu })\widehat{\Phi },&-\infty \lt x\lt R_0 \end{cases} \end{eqnarray}
and
Since
![]() $\left(\widehat{\Phi },\widehat{\Psi }\right)\preceq (0,0)$
for
$\left(\widehat{\Phi },\widehat{\Psi }\right)\preceq (0,0)$
for
![]() $x\lt R_0$
and (4.17) holds true, there exist
$x\lt R_0$
and (4.17) holds true, there exist
![]() $\zeta _1,\zeta _2\in \mathbb R$
such that
$\zeta _1,\zeta _2\in \mathbb R$
such that
Then, (4.15) is equivalent to
Suppose
![]() $\widehat{\Phi }(\zeta _1)\lt 0$
. We can obtain a contradiction by distinguishing the following two cases:
$\widehat{\Phi }(\zeta _1)\lt 0$
. We can obtain a contradiction by distinguishing the following two cases:
-
(i)
 $[b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _2)\lt 0$
;
$[b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _2)\lt 0$
; -
(ii)
 $[b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _2)\geq 0$
.
$[b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _2)\geq 0$
.
When case (i) happens, in view of (4.14) and
![]() $\left(\widehat{\Phi },\widehat{\Psi }\right)(x)\preceq (0,0)$
for
$\left(\widehat{\Phi },\widehat{\Psi }\right)(x)\preceq (0,0)$
for
![]() $x\lt R_0$
, one can use the equation for
$x\lt R_0$
, one can use the equation for
![]() $\widehat{\Phi }$
in (4.16) to deduce
$\widehat{\Phi }$
in (4.16) to deduce
 \begin{eqnarray*} \begin{aligned} 0\leq &\ d_1 \widehat{\Phi }_{xx}(\zeta _1)+c_\nu \widehat{\Phi }_x(\zeta _1)\\ \leq &\ [b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _1)\\ \leq &\ [b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _2)\lt 0, \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} 0\leq &\ d_1 \widehat{\Phi }_{xx}(\zeta _1)+c_\nu \widehat{\Phi }_x(\zeta _1)\\ \leq &\ [b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _1)\\ \leq &\ [b_1+a_1(M^\ast -\epsilon _0)]\widehat{\Phi }(\zeta _1)-a_1(e_1-H^\ast +\epsilon _0)\widehat{\Psi }(\zeta _2)\lt 0, \end{aligned} \end{eqnarray*}
which is a contradiction, and hence case (i) is impossible.
If case (ii) happens, one can use (4.14) and the equation of
![]() $\widehat{\Psi }$
in (4.16) to deduce
$\widehat{\Psi }$
in (4.16) to deduce
 \begin{eqnarray*} \begin{aligned} 0\leq &\ d_2 \widehat{\Psi }_{xx}(\zeta _2)+c_\nu \widehat{\Psi }_x(\zeta _2)\\ \leq &\ [b_2+a_2(H^\ast -\epsilon _0)]\widehat{\Psi }(\zeta _2)-a_2(e_2-M^\ast +\epsilon _0)\widehat{\Phi }(\zeta _2)\\ \leq &\ [b_2+a_2(H^\ast -\epsilon _0)]\widehat{\Psi }(\zeta _2)-a_2(e_2-M^\ast +\epsilon _0)\widehat{\Phi }(\zeta _1)\\ =&\ \frac{\widehat{\Phi }(\zeta _1)}{a_1(e_1-H^\ast +\epsilon _0)}\Big \{\frac{a_1(e_1-H^\ast +\epsilon _0)}{\widehat{\Phi }(\zeta _1)}\widehat{\Psi }(\zeta _2) [b_2+a_2(H^\ast -2\epsilon _0)]\\ &\ \def\lumina\hspace{3cm} -{a_1(e_1-H^\ast +\epsilon _0)}a_2(e_2-M^\ast +\epsilon _0)\Big \}\\ \leq &\ \frac{\widehat{\Phi }(\zeta _1)}{a_1(e_1-H^\ast +\epsilon _0)} A(\epsilon _0)\ (\mbox{due to the assumption in case (ii)}), \end{aligned} \end{eqnarray*}
\begin{eqnarray*} \begin{aligned} 0\leq &\ d_2 \widehat{\Psi }_{xx}(\zeta _2)+c_\nu \widehat{\Psi }_x(\zeta _2)\\ \leq &\ [b_2+a_2(H^\ast -\epsilon _0)]\widehat{\Psi }(\zeta _2)-a_2(e_2-M^\ast +\epsilon _0)\widehat{\Phi }(\zeta _2)\\ \leq &\ [b_2+a_2(H^\ast -\epsilon _0)]\widehat{\Psi }(\zeta _2)-a_2(e_2-M^\ast +\epsilon _0)\widehat{\Phi }(\zeta _1)\\ =&\ \frac{\widehat{\Phi }(\zeta _1)}{a_1(e_1-H^\ast +\epsilon _0)}\Big \{\frac{a_1(e_1-H^\ast +\epsilon _0)}{\widehat{\Phi }(\zeta _1)}\widehat{\Psi }(\zeta _2) [b_2+a_2(H^\ast -2\epsilon _0)]\\ &\ \def\lumina\hspace{3cm} -{a_1(e_1-H^\ast +\epsilon _0)}a_2(e_2-M^\ast +\epsilon _0)\Big \}\\ \leq &\ \frac{\widehat{\Phi }(\zeta _1)}{a_1(e_1-H^\ast +\epsilon _0)} A(\epsilon _0)\ (\mbox{due to the assumption in case (ii)}), \end{aligned} \end{eqnarray*}
where
From
![]() $\mathcal R_0\gt 1$
, we easily see by direct computation that
$\mathcal R_0\gt 1$
, we easily see by direct computation that
![]() $A(0)=a_1a_2e_1e_2-b_1b_2\gt 0$
. Therefore, by the continuity of
$A(0)=a_1a_2e_1e_2-b_1b_2\gt 0$
. Therefore, by the continuity of
![]() $A(\epsilon _0)$
with respect to
$A(\epsilon _0)$
with respect to
![]() $\epsilon _0$
, we have
$\epsilon _0$
, we have
![]() $A(\epsilon _0)\gt 0$
by taking
$A(\epsilon _0)\gt 0$
by taking
![]() $\epsilon _0\gt 0$
small enough, which yields
$\epsilon _0\gt 0$
small enough, which yields
Again, we arrive at a contradiction. Therefore,
![]() $\widehat{\Phi }(\zeta _1)=0$
, or equivalently,
$\widehat{\Phi }(\zeta _1)=0$
, or equivalently,
![]() $\widehat{\Phi }(x)=0$
for
$\widehat{\Phi }(x)=0$
for
![]() $x\lt R_0$
. Similarly, we can prove
$x\lt R_0$
. Similarly, we can prove
![]() $\widehat{\Psi }(x)=0$
for
$\widehat{\Psi }(x)=0$
for
![]() $x\lt R_0$
by repeating the above arguments. Thus, (4.15) holds.
$x\lt R_0$
by repeating the above arguments. Thus, (4.15) holds.
We are now ready to reach a contradiction by considering
![]() $(\Phi,\Psi )(x,t)$
, which satisfies the first two equations in (4.11). Moreover, for any
$(\Phi,\Psi )(x,t)$
, which satisfies the first two equations in (4.11). Moreover, for any
![]() $t\in \mathbb{R}$
and
$t\in \mathbb{R}$
and
![]() $x\leq R^*$
,
$x\leq R^*$
,
 \begin{align*} &(\Phi,\Psi )(x,t)\succeq \left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x),\\ &\Phi (R_0,t)\succeq u_{c_\nu }(R^\ast -R_0)-\omega _1(R_0)\succeq u_{c_\nu }(R^\ast -R_0+\epsilon ),\\ &\Psi (R_0,t)\succeq v_{c_\nu }(R^\ast -R_0)-\omega _2(R_0)\succeq v_{c_\nu }(R^\ast -R_0+\epsilon ). \end{align*}
\begin{align*} &(\Phi,\Psi )(x,t)\succeq \left ( u_{c_\nu },v_{c_\nu }\right )(R^\ast -x),\\ &\Phi (R_0,t)\succeq u_{c_\nu }(R^\ast -R_0)-\omega _1(R_0)\succeq u_{c_\nu }(R^\ast -R_0+\epsilon ),\\ &\Psi (R_0,t)\succeq v_{c_\nu }(R^\ast -R_0)-\omega _2(R_0)\succeq v_{c_\nu }(R^\ast -R_0+\epsilon ). \end{align*}
Therefore, we can use the comparison principle to deduce that
which is equivalent to
Letting
![]() $s\rightarrow -\infty$
, due to (4.15) we obtain
$s\rightarrow -\infty$
, due to (4.15) we obtain
By Step 2,
Taking
![]() $\epsilon _1\in (0,\epsilon ]$
small enough, we have, for
$\epsilon _1\in (0,\epsilon ]$
small enough, we have, for
![]() $x\in [R_0,R^\ast +\epsilon _1]$
,
$x\in [R_0,R^\ast +\epsilon _1]$
,
Hence, for
![]() $x\in [R_0,R^\ast +\epsilon _1]$
and
$x\in [R_0,R^\ast +\epsilon _1]$
and
![]() $t\in \mathbb{R}$
,
$t\in \mathbb{R}$
,
Combining this with (4.18), we obtain
for all small
![]() $\epsilon _1\in (0,\epsilon )$
, which contradicts the definition of
$\epsilon _1\in (0,\epsilon )$
, which contradicts the definition of
![]() $R^\ast$
. This completes the proof.
$R^\ast$
. This completes the proof.
Proposition 4.3.
![]() $(\Phi,\Psi )(x,t)\equiv (u_{c_\nu },v_{c_\nu })(R^\ast -x)$
and
$(\Phi,\Psi )(x,t)\equiv (u_{c_\nu },v_{c_\nu })(R^\ast -x)$
and
![]() $L(t)\equiv R^*$
.
$L(t)\equiv R^*$
.
Proof. We already know that
![]() $R^*=L(0)=\min L(t)$
and
$R^*=L(0)=\min L(t)$
and
with
It follows from the strong maximum principle for cooperative systems and the Hopf boundary lemma that
On the other hand,
![]() $L^{\prime}(0)=0$
implies, by the last identity in (4.2),
$L^{\prime}(0)=0$
implies, by the last identity in (4.2),
Thus, we must have
![]() $(\Phi,\Psi )(x,t)\equiv (u_{c_\nu },v_{c_\nu })(R^\ast -x)$
, which implies
$(\Phi,\Psi )(x,t)\equiv (u_{c_\nu },v_{c_\nu })(R^\ast -x)$
, which implies
![]() $L(t)\equiv L(0)$
.
$L(t)\equiv L(0)$
.
4.3. Proof of Theorem 1.2
We are now ready to complete the proof of Theorem 1.2. For clarity, we achieve this goal by first proving two claims.
Claim 1: Let
![]() $\{t_n\}$
be the sequence in Lemma 4.1
. Then for every
$\{t_n\}$
be the sequence in Lemma 4.1
. Then for every
![]() $t\in \mathbb R$
,
$t\in \mathbb R$
,
![]() $\lim _{n\rightarrow \infty }h^{\prime}(t+t_n)=c_\nu$
. Moreover, (1.8) holds along
$\lim _{n\rightarrow \infty }h^{\prime}(t+t_n)=c_\nu$
. Moreover, (1.8) holds along
![]() $t=t_n$
.
$t=t_n$
.
It follows from Lemma 4.1 and Proposition 4.3 that
![]() $h(t+t_n)-k(t+t_n)\rightarrow L(0)=R^*$
in
$h(t+t_n)-k(t+t_n)\rightarrow L(0)=R^*$
in
![]() $C_{loc}^{1+\frac{\alpha }{2}}(\mathbb{R})$
. Hence,
$C_{loc}^{1+\frac{\alpha }{2}}(\mathbb{R})$
. Hence,
![]() $h^{\prime}(t+t_n)\rightarrow c_\nu$
in
$h^{\prime}(t+t_n)\rightarrow c_\nu$
in
![]() $C_{loc}^{\frac{\alpha }{2}}(\mathbb{R}).$
It then follows easily from Lemma 4.1 and Proposition 4.3 that
$C_{loc}^{\frac{\alpha }{2}}(\mathbb{R}).$
It then follows easily from Lemma 4.1 and Proposition 4.3 that
Hence, for any
![]() $L_0\gt 0$
,
$L_0\gt 0$
,
On the other hand, for any given small
![]() $\epsilon \gt 0$
, by Lemmas 3.2 and 3.4, there exists
$\epsilon \gt 0$
, by Lemmas 3.2 and 3.4, there exists
![]() $L_1\gt 0$
and some large integer
$L_1\gt 0$
and some large integer
![]() $N\geq 1$
such that
$N\geq 1$
such that
Clearly, for
![]() $L_2\gt 0$
large,
$L_2\gt 0$
large,
Therefore, if we take
![]() $L_0=\max \{L_1, L_2\}$
, then for
$L_0=\max \{L_1, L_2\}$
, then for
![]() $n\geq N$
,
$n\geq N$
,
It follows that
Consider (1.3) with initial function
![]() $(H_0(\!-x), M_0(\!-x))$
, the above proved conclusions imply that
$(H_0(\!-x), M_0(\!-x))$
, the above proved conclusions imply that
Claim 2:
![]() $\lim _{t\rightarrow \infty }(h(t)-c_\nu t)=h^*\,:\!=R^\ast -2C=L(0)-2C$
.
$\lim _{t\rightarrow \infty }(h(t)-c_\nu t)=h^*\,:\!=R^\ast -2C=L(0)-2C$
.
By Claim 1, along a sequence
![]() $\{t_n\}$
satisfying
$\{t_n\}$
satisfying
(4.19) holds and
Let us note that
If the desired conclusion does not hold, then
![]() $\limsup _{t\to \infty }(h(t)-c_\nu t)=\tilde h^*\gt h^*$
. Thus, we can find a sequence
$\limsup _{t\to \infty }(h(t)-c_\nu t)=\tilde h^*\gt h^*$
. Thus, we can find a sequence
![]() $\{s_n\}$
increasing to
$\{s_n\}$
increasing to
![]() $+\infty$
as
$+\infty$
as
![]() $n\to \infty$
such that
$n\to \infty$
such that
We now examine
![]() $(\overline H,\overline M, \overline g,\overline h)$
defined in (3.1). Take
$(\overline H,\overline M, \overline g,\overline h)$
defined in (3.1). Take
![]() $X_0=(\tilde h^*-h^*)/4\gt 0$
and
$X_0=(\tilde h^*-h^*)/4\gt 0$
and
![]() $T^*=t_n$
. Then take
$T^*=t_n$
. Then take
![]() $\sigma =(\tilde h^*-h^*)/4\gt 0$
and choose
$\sigma =(\tilde h^*-h^*)/4\gt 0$
and choose
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
![]() $K_1\gt 0$
such that (3.9), (3.12) and (3.13) hold. As in the proof of Lemma 3.2, by direct calculations we see that (3.3), (3.4), (3.5), (3.6) and (3.7) hold.
$K_1\gt 0$
such that (3.9), (3.12) and (3.13) hold. As in the proof of Lemma 3.2, by direct calculations we see that (3.3), (3.4), (3.5), (3.6) and (3.7) hold.
We show next that for all large
![]() $n$
, due to (4.19) and (4.20), the inequalities in (3.8) hold as well, and therefore the comparison principle can be applied to conclude that
$n$
, due to (4.19) and (4.20), the inequalities in (3.8) hold as well, and therefore the comparison principle can be applied to conclude that
Indeed, for
![]() $x\in [\overline{g}(t_n),h(t_n)]=[g(t_n), h(t_n)]$
, by (4.19) and (4.20), we have
$x\in [\overline{g}(t_n),h(t_n)]=[g(t_n), h(t_n)]$
, by (4.19) and (4.20), we have
 \begin{equation*}\begin {aligned} \overline {H}(x,t_n)&=(1+K_1)u_{c_\nu }(\bar {h}(t_n)-x)\\ &=(1+K_1)u_{c_\nu }(h(t_n)+X_0-x)\\ &\geq H(x, t_n) \mbox { for all large } n, \end {aligned} \end{equation*}
\begin{equation*}\begin {aligned} \overline {H}(x,t_n)&=(1+K_1)u_{c_\nu }(\bar {h}(t_n)-x)\\ &=(1+K_1)u_{c_\nu }(h(t_n)+X_0-x)\\ &\geq H(x, t_n) \mbox { for all large } n, \end {aligned} \end{equation*}
and
 \begin{equation*}\begin {aligned} \overline {M}(x,t_n)&=(1+K_1)v_{c_\nu }(\bar {h}(t_n)-x)\\ &=(1+K_1)v_{c_\nu }(h(t_n)+X_0-x)\\ &\geq M(x, t_n) \mbox { for all large } n. \end {aligned} \end{equation*}
\begin{equation*}\begin {aligned} \overline {M}(x,t_n)&=(1+K_1)v_{c_\nu }(\bar {h}(t_n)-x)\\ &=(1+K_1)v_{c_\nu }(h(t_n)+X_0-x)\\ &\geq M(x, t_n) \mbox { for all large } n. \end {aligned} \end{equation*}
Hence, (4.22) holds for all large
![]() $n$
, say
$n$
, say
![]() $n\geq N=N(K_1, X_0)$
. In particular, for all large integer
$n\geq N=N(K_1, X_0)$
. In particular, for all large integer
![]() $k$
satisfying
$k$
satisfying
![]() $s_k\geq t_n$
we have
$s_k\geq t_n$
we have
It follows that
Letting
![]() $n\to \infty$
we then obtain
$n\to \infty$
we then obtain
which is impossible.
Thus, we have proved Claim 2 and then any positive sequence
![]() $\{t_n\}$
converging to
$\{t_n\}$
converging to
![]() $+\infty$
can be used in Lemma 4.1, and so it has a subsequence such that (4.21) and (4.19) hold. This clearly implies that the second part in (1.7) and (1.8) holds.
$+\infty$
can be used in Lemma 4.1, and so it has a subsequence such that (4.21) and (4.19) hold. This clearly implies that the second part in (1.7) and (1.8) holds.
As before, consider (1.3) with initial function
![]() $(H_0(\!-x), M_0(\!-x))$
; the above proved conclusions imply that the first part in (1.7) and (1.8) holds as well. Theorem 1.2 is now proved.
$(H_0(\!-x), M_0(\!-x))$
; the above proved conclusions imply that the first part in (1.7) and (1.8) holds as well. Theorem 1.2 is now proved.
Acknowledgements
This work was supported by the Natural Science Foundation of China (12071270,12371496) and the Natural Science Basic Research Program of Shaanxi (2023-JC-JQ-03). Y. Du was also supported by the Australian Research Council. We are grateful to the referees for their detailed suggestions to improve the presentation of the paper.
Competing interests
None.