No CrossRef data available.
Article contents
On the Lie symmetries of characteristic function hierarchy in compressible turbulence
Published online by Cambridge University Press: 11 April 2022
Abstract
We compute the Lie symmetries of characteristic function (CF) hierarchy of compressible turbulence, ignoring the effects of viscosity and heat conductivity. In the probability density function (PDF) hierarchy, a typical non-local nature is observed, which is naturally eliminated in the CF hierarchy. We observe that the CF hierarchy retains all the symmetries satisfied by compressible Euler equations. Broadly speaking, four types of symmetries can be discerned in the CF hierarchy: (i) symmetries corresponding to coordinate system invariance, (ii) scaling/dilation groups, (iii) projective groups and (iv) statistical symmetries, where the latter define measures of intermittency and non-gaussianity. As the multi-point CFs need to satisfy additional constraints such as the reduction condition, the projective symmetries are only valid for monatomic gases, that is, the specific heat ratio, 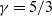 $\gamma = 5/3$. The linearity of the CF hierarchy results in the statistical symmetries due to the superposition principle. For all of the symmetries, the global transformations of the CF and various key compressible statistics are also presented.
$\gamma = 5/3$. The linearity of the CF hierarchy results in the statistical symmetries due to the superposition principle. For all of the symmetries, the global transformations of the CF and various key compressible statistics are also presented.
MSC classification
- Type
- Papers
- Information
- European Journal of Applied Mathematics , Volume 34 , Special Issue 5: Symmetries and Differential Equations , October 2023 , pp. 913 - 935
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press



