Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T08:19:59.908Z Has data issue: false hasContentIssue false
  • English
  • Français

On steady states of van der Waals force driven thin film equations

Published online by Cambridge University Press:  01 April 2007

HUIQIANG JIANG  and
WEI-MING NI
HUIQIANG JIANG
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA email: [email protected]
WEI-MING NI
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

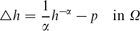Let , N ≥2 be a bounded smooth domain and α > 1. We are interested in the singular elliptic equation with Neumann boundary conditions. In this paper, a complete description of all continuous radially symmetric solutions is given. In particular, we construct nontrivial smooth solutions as well as rupture solutions. Here a continuous solution is said to be a rupture solution if its zero set is nonempty. When N = 2 and α = 3, the equation is used to model steady states of van der Waals force driven thin films of viscous fluids. We also consider the physical problem when total volume of the fluid is prescribed.

Type
Papers
Information
European Journal of Applied Mathematics , Volume 18 , Issue 2 , April 2007 , pp. 153 - 180
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Almgren, R., Bertozzi, A. & Brenner, M. P. (1996) Stable and unstable singularities in the unforced Hele-Shaw cell. Phys. Fluids 8 (6), 1356–1370.CrossRefGoogle Scholar
[2]Barenblatt, G. I., Beretta, E. & Bertsch, M. (1997) The problem of the spreading of a liquid film along a solid surface: a new mathematical formulation. Proc. Natl. Acad. Sci. U.S.A. 94 (19), 10024–10030.CrossRefGoogle ScholarPubMed
[3]Beretta, E. (1997) Selfsimilar source solutions of a fourth order degenerate parabolic equation. Nonlinear Anal. 29 (7), 741–760.CrossRefGoogle Scholar
[4]Bernoff, A. J. & Bertozzi, A. L. (1995) Singularities in a modified Kuramoto-Sivashinsky equation describing interface motion for phase transition. Physica D 85 (3), 375–404.CrossRefGoogle Scholar
[5]Bertozzi, A. L., Grün, G. & Witelski, T. P. (2001) Dewetting films: bifurcations and concentrations. Nonlinearity 14 (6), 1569–1592.Google Scholar
[6]Bertozzi, A. L. & Pugh, M. (1996) The lubrication approximation for thin viscous films: regularity and long-time behavior of weak solutions. Commun. Pure Appl. Math. 49 (2), 85–123.3.0.CO;2-2>CrossRefGoogle Scholar
[7]Bertozzi, A. L. & Pugh, M. C. (2000) Finite-time blow-up of solutions of some long-wave unstable thin film equations. Indiana Univ. Math. J. 49 (4), 1323–1366.CrossRefGoogle Scholar
[8]Bertozzi, A. L. (1998) The mathematics of moving contact lines in thin liquid films. Notices Am. Math. Soc. 45 (6), 689–697.Google Scholar
[9]Bertozzi, A. L., Brenner, M. P., Dupont, T. F. & Kadanoff, L. P. (1994) Singularities and similarities in interface flows. In: Trends and Perspectives in Applied Mathematics. Appl. Math. Sci. 100, 155–208. Springer, New York.CrossRefGoogle Scholar
[10]Bertsch, M., Dal Passo, R., Garcke, H. & Grün, G. (1998) The thin viscous flow equation in higher space dimensions. Adv. Differential Equations 3 (3), 417–440.CrossRefGoogle Scholar
[11]Constantin, P., Dupont, T. F., Goldstein, R. E., Kadanoff, L. P., Shelley, M. J. & Zhou, S.-M. (1993) Droplet breakup in a model of the Hele-Shaw cell. Phys. Rev. E (3), 47 (6), 4169–4181.CrossRefGoogle Scholar
[12]Dal, Passo, R., Garcke, H. & Grün, G. (1998) On a fourth-order degenerate parabolic equation: global entropy estimates, existence, and qualitative behavior of solutions. SIAM J. Math. Anal. 29 (2), 321–342 (electronic).Google Scholar
del Pino, M. A. & Hernandez, G. E. (1996) Solvability of the Neumann problem in a ball for −Δ u + u−v = h(|x|), v>1. J. Differential Equations 124 (1), 108–131.CrossRefGoogle Scholar
[13]Dupont, T. F., Goldstein, R. E., Kadanoff, L. P. & Zhou, S.-M. (1993) Finite-time singularity formation in Hele-Shaw systems. Phys. Rev. E (3) 47 (6), 4182–4196.CrossRefGoogle ScholarPubMed
[14]Ehrhard, P. (1994) The spreading of hanging drops. J. Colloid Interface 168 (1), 242–246.CrossRefGoogle Scholar
[15]Grün, G. (2004) Droplet spreading under weak slippage—existence for the Cauchy problem. Commun. Partial Differential Equations 29 (11–12), 1697–1744.CrossRefGoogle Scholar
[16]Hartman, P. (1964) Ordinary Differential Equations, Wiley, New York.Google Scholar
[17]Jiang, H. & Lin, F. (2004) Zero set of Sobolev functions with negative power of integrability. Chin. Ann. Math. Ser. B 25 (1), 65–72.CrossRefGoogle Scholar
[18]Laugesen, R. S. & Pugh, M. C. (2000) Linear stability of steady states for thin film and Cahn-Hilliard type equations. Arch. Ration. Mech. Anal. 154 (1), 3–51.CrossRefGoogle Scholar
[19]Laugesen, R. S. & Pugh, M. C. (2000) Properties of steady states for thin film equations. Eur. J. Appl. Math. 11 (3), 293–351.CrossRefGoogle Scholar
[20]Laugesen, R. S. & Pugh, M. C. (2002) Energy levels of steady states for thin-film-type equations. J. Differential Equations 182 (2), 377–415.CrossRefGoogle Scholar
[21]Laugesen, R. S. & Pugh, M. C. (2002) Heteroclinic orbits, mobility parameters and stability for thin film type equations. Electron. J. Differential Equations 95, 29 pp. (electronic).Google Scholar
[22]Myers, T. G. (1998) Thin films with high surface tension. SIAM Rev. 40 (3), 441–462 (electronic).CrossRefGoogle Scholar
[23]Oron, A., Davis, S. H. & Bankoff, S. G. (1997) Nonlinear theory of film rupture. Rev. Mod. Phys. 69 (3), 931–980.CrossRefGoogle Scholar
[24]Shelley, M. J., Goldstein, R. E. & Pesci, A. I. (1993) Topological transitions in Hele-Shaw flow. In: Singularities in Fluids, Plasmas and Optics (Heraklion, 1992), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 404, 167–188. Kluwer Acad. Publ., Dordrecht.CrossRefGoogle Scholar
[25]Slepčev, D. & Pugh, M. C. (2005) Selfsimilar blowup of unstable thin-film equations. Indiana Univ. Math. J. 54 (6), 1697–1738.Google Scholar
[26]Williams, M. B. & Davis, S. H. (1982) Nonlinear theory of film rupture. J. Colloid Interface. Sci. 90 (1), 220–228.CrossRefGoogle Scholar
[27]Witelski, T. P. & Bernoff, A. J. (1999) Stability of self-similar solutions for van der {W}aals driven thin film rupture. Phys. Fluids 11 (9), 2443–2445.CrossRefGoogle Scholar
[28]Witelski, T. P. & Bernoff, A. J. (2000) Dynamics of three-dimensional thin film rupture. Physica. D 147 (1–2), 155–176.CrossRefGoogle Scholar
[29]Zhang, W. W. & Lister, J. R. (1999) Similarity solutions for van der {W}aals rupture of a thin film on a solid substrate. Phys. Fluids 11 (9), 2454–2462.CrossRefGoogle Scholar