Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T06:16:32.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear evolution equations on the half-line with dynamic boundary conditions

Part of: Harmonic analysis in one variable Partial differential equations Equations of mathematical physics and other areas of application General theory in ordinary differential equations General higher-order equations and systems Equations and systems with constant coefficients

Published online by Cambridge University Press:  03 May 2021

D. A. SMITH Open the ORCID record for D. A. SMITH [Opens in a new window]  and
W. Y. TOH
D. A. SMITH
Affiliation:
Yale-NUS College, Singapore 138533, Singapore emails: [email protected]; [email protected]
W. Y. TOH
Affiliation:
Yale-NUS College, Singapore 138533, Singapore emails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The classical half-line Robin problem for the heat equation may be solved via a spatial Fourier transform method. In this work, we study the problem in which the static Robin condition 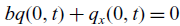$$bq(0,t) + {q_x}(0,t) = 0$$ is replaced with a dynamic Robin condition; 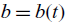$$b = b(t)$$ is allowed to vary in time. Applications include convective heating by a corrosive liquid. We present a solution representation and justify its validity, via an extension of the Fokas transform method. We show how to reduce the problem to a variable coefficient fractional linear ordinary differential equation for the Dirichlet boundary value. We implement the fractional Frobenius method to solve this equation and justify that the error in the approximate solution of the original problem converges appropriately. We also demonstrate an argument for existence and unicity of solutions to the original dynamic Robin problem for the heat equation. Finally, we extend these results to linear evolution equations of arbitrary spatial order on the half-line, with arbitrary linear dynamic boundary conditions.

Keywords

Partial differential equationtime-dependent boundary conditionFokas transform methodfractional differential equation

MSC classification

Primary: 35A22: Transform methods (e.g. integral transforms) 34A08: Fractional differential equations 35G16: Initial-boundary value problems for linear higher-order equations 35E15: Initial value problems 35Q79: PDEs in connection with classical thermodynamics and heat transfer
Secondary: 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type
Type
Papers
Information
European Journal of Applied Mathematics , Volume 33 , Issue 3 , June 2022 , pp. 505 - 537
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aitzhan, S., Bhandari, S. & Smith, D. A. (2020) Fokas diagonalization of piecewise constant coefficient linear differential operators on finite intervals and networks (submitted) arXiv:2012.05638 [math.SP].Google Scholar
Ashton, A. C. L. (2012) On the rigorous foundations of the Fokas method for linear elliptic partial differential equations. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 468(2141), 1325–1331.Google Scholar
Baleanu, D., Fernandez, A. & Fokas, A. S. (2018) Solving PDEs of fractional order using the unified transform method. Appl. Math. Comput. 339, 738–749.Google Scholar
Becker, N. M., Bivins, R. L., Hsu, Y. C., Murphy, H. D., WhiteJr., A. B. & Wing, G. M. (1983) Heat diffusion with time-dependent convective boundary conditions. Int. J. Num. Methods Eng. 19, 1871–1880.Google Scholar
Biondini, G. & Trogdon, T. (2019) Evolution partial differential equations with discontinuous data. Quart. Appl. Math. 77, 689–726.Google Scholar
Bobyk, B. Ya., Shvets’, R. M. & Yatskiv, O. I. (2012) Thermostressed state of a cylinder with thin near-surface layer having time-dependent thermophysical properties. J. Math. Sci. 187, 647–666.Google Scholar
Chen, H. T., Sun, S. L., Huang, H. C. & Lee, S. Y. (2010) Analytic closed solution for the heat conduction with time dependent heat convection coefficient at one boundary. Comput. Model. Eng. Sci. 59(2), 107–126.Google Scholar
Colbrook, M. J. (2020) Extending the unified transform: curvilinear polygons and variable coefficient PDEs. IMA J. Num. Anal. 40, 976–1004.CrossRefGoogle Scholar
Colbrook, M. J., Flyer, N. & Fornberg, B. (2018) On the Fokas method for the solution of elliptic problems in both convex and non-convex polygonal domains. J. Comp. Phys. 374, 996–1016.CrossRefGoogle Scholar
Colbrook, M. J., Fokas, A. S. & Hashemzadeh, P. (2019) A hybrid analytical-numerical technique for elliptic PDEs. SIAM J. Sci. Comp. 41, A1066–A1090.CrossRefGoogle Scholar
Crowdy, D. G. (2015) A transform method for Laplace’s equation in multiply connected circular domains. IMA J. Appl. Math. 80, 1902–1931.Google Scholar
Crowdy, D. G. & Luca, E. (2018) A transform method for the biharmonic equation in multiply connected circular domains. IMA J. Appl. Math. 83, 942–976.Google Scholar
Deconinck, B., Pelloni, B. & Sheils, N. E. (2014) Non-steady-state heat conduction in composite walls. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 470(2165), 20130605.CrossRefGoogle Scholar
Deconinck, B. & Sheils, N. E. (2020) The time-dependent Schrödinger equation with piecewise constant potentials. E. J. Appl. Math. 31, 57–83.Google Scholar
Deconinck, B., Sheils, N. E. & Smith, D. A. (2016) The linear KdV equation with an interface. Comm. Math. Phys. 347, 489–509.CrossRefGoogle Scholar
Deconinck, B., Trogdon, T. & Vasan, V. (2014) The method of Fokas for solving linear partial differential equations. SIAM Rev. 56(1), 159–186.CrossRefGoogle Scholar
Diethelm, K. (2010) The Analysis of Fractional Differential Equations, Courant Lecture Notes in Mathematics, Springer-Verlag, Berlin, Heidelberg.CrossRefGoogle Scholar
Fokas, A. S. (2001) Two dimensional linear partial differential equations in a convex polygon. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 457, 371–393.Google Scholar
Fokas, A. S. (2002) Integrable nonlinear evolution equations on the half-line. Comm. Math. Phys. 230(1), 1–39.Google Scholar
Fokas, A. S. (2002) A new transform method for evolution PDEs. IMA J. Appl. Math. 67, 559–590.CrossRefGoogle Scholar
Fokas, A. S. A Unified Approach to Boundary Value Problems, CBMS-SIAM, 2008.Google Scholar
Fokas, A. S., Its, A. R. & Sung, L. Y. (2005) The nonlinear Schrödinger equation on the half-line. Nonlinearity 18(4), 1771–1822.Google Scholar
Fokas, A. S. & Kalimeris, K. (2014) Eigenvalues for the Laplace operator in the interior of an equilateral triangle. Comput. Methods Funct. Theory 14, 1–33.CrossRefGoogle Scholar
Fokas, A. S. & Lenells, J. (2011) Boundary-value problems for the stationary axisymmetric Einstein equations: a rotating disc. Nonlinearity 24(1), 177–206.Google Scholar
Fokas, A. S., Lenells, J. & Pelloni, B. (2013) Boundary value problems for the elliptic sine-Gordon equation in a semi-strip. J. Nonlinear Sci. 23, 241–282.CrossRefGoogle Scholar
Fokas, A. S. & Mantzavinos, D. (2013) The unified method for the heat equation: I. Non-separable boundary conditions and non-local constraints in one dimension. Eur. J. Appl. Math. 24, 857–886.Google Scholar
Fokas, A. S. & Mantzavinos, D. (2015) The unified method for the heat equation: II. Non-separable boundary conditions in two dimensions. E. J. Appl. Math. 26, 887–916.Google Scholar
Fokas, A. S. & Pelloni, B. (2001) Two-point boundary value problems for linear evolution equations. Math. Proc. Cambridge Philos. Soc. 131, 521–543.CrossRefGoogle Scholar
Fokas, A. S. & Pelloni, B. (eds.) (2015) Unified Transform for Boundary Value Problems: Applications and Advances, SIAM.CrossRefGoogle Scholar
Fokas, A. S. & Smith, D. A. (2016) Evolution PDEs and augmented eigenfunctions. Finite interval. Adv. Differ. Equations 21(7/8), 735–766.Google Scholar
Fokas, A. S. & Spence, E. A. (2012) Synthesis, as opposed to separation, of variables. SIAM Rev. 54(2), 291–324.CrossRefGoogle Scholar
Fokas, A. S. & Sung, L. Y. (1999) Initial-boundary value problems for linear dispersive evolution equations on the half-line (unpublished).Google Scholar
Govindarajan, R., Prasath, S. G. & Vasan, V. (2019) Accurate solution method for the Maxey-Riley equation, and the effects of Basset history. J. Fluid Mech. 868, 428–460.Google Scholar
Holy, Z. J. (1972) Temperature and stresses in reactor fuel elements due to time- and space-dependent heat-transfer coefficients. Nuclear Eng. Des. 18, 145–197.CrossRefGoogle Scholar
Ivanov, V. V. & Salomatov, V. V. (1965) On the calculation of the temperature field in solids with variable heat-transfer coefficients. J. Eng. Phys. 9, 63–64.Google Scholar
Ivanov, V. V. & Salomatov, V. V. (1966) Unsteady temperature field in solid bodies with variable heat transfer coefficient. J. Eng. Phys. 11, 151–152.CrossRefGoogle Scholar
Jackson, D. (1915) Expansion problems with irregular boundary conditions. Proc. Am. Acad. Arts Sci. 51(7), 383–417.CrossRefGoogle Scholar
Kilbas, A. A., Marichev, O. I. & Samko, S. G. (2002) Fractional Integrals and Derivatives: Theory and Applications, Taylor & Francis, London.Google Scholar
Kilbas, A. A., Srivastava, H. M. & Trujillo, J. J. (2006) Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies, vol. 204, Elsevier.Google Scholar
Kozlov, V. N. (1970) Solution of heat-conduction problem with variable heat-exchange coefficient. J. Eng. Phys. 18, 100–104.Google Scholar
Lee, S. Y. & Tu, T. W. (2015) Unsteady temperature field in slabs with different kinds of time-dependent boundary conditions. Acta Mechanica 226, 3597–3609.CrossRefGoogle Scholar
Miller, P. D. & Smith, D. A. (2018) The diffusion equation with nonlocal data. J. Math. Anal. Appl. 466(2), 1119–1143.CrossRefGoogle Scholar
Moitsheki, R. J. (2008) Transient heat diffusion with temperature-dependent conductivity and time-dependent heat transfer coefficient. Math. Problems Eng. 2008(347568), 1–9.CrossRefGoogle Scholar
Özişik, M. N. & Murray, R. L. (1974) On the solution of linear diffusion problems with variable boundary condition parameters. J. Heat Transfer 96(1), 48–51.CrossRefGoogle Scholar
Pelloni, B. (2004) Well-posed boundary value problems for linear evolution equations on a finite interval. Math. Proc. Cambridge Philos. Soc. 136, 361–382.CrossRefGoogle Scholar
Pelloni, B. & Pinotsis, D. A. (2010) The elliptic sine-Gordon equation in a half plane. Nonlinearity 23(1), 77.CrossRefGoogle Scholar
Pelloni, B. & Smith, D. A. (2013) Spectral theory of some non-selfadjoint linear differential operators. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 469(2154), 20130019.CrossRefGoogle Scholar
Pelloni, B. & Smith, D. A. (2016) Evolution PDEs and augmented eigenfunctions. Half line. J. Spectr. Theory 6, 185–213.Google Scholar
Pelloni, B. & Smith, D. A. (2018) Nonlocal and multipoint boundary value problems for linear evolution equations. Stud. Appl. Math. 141(1), 46–88.CrossRefGoogle Scholar
Pinsky, M. A. (2011) Paryial Differential Equations and Boundary-Value Problems, Pure and Applied Undergraduate Texts, American Mathematical Society, Providence, Rhode Island, USA.Google Scholar
Postol’nik, Yu. S. (1970) One-dimensional convective heating with a time-dependent heat-transfer coefficient. J. Eng. Phys. 18, 233–238.CrossRefGoogle Scholar
Sheils, N. E. & Deconinck, B. (2015) Interface problems for dispersive equations. Stud. Appl. Math. 134(3), 253–275.CrossRefGoogle Scholar
Sheils, N. E. & Smith, D. A. (2015) Heat equation on a network using the Fokas method. J. Phys. A Math. Theor. 48(33), 21 pp.Google Scholar
Smith, D. A. (2012) Well-posed two-point initial-boundary value problems with arbitrary boundary conditions. Math. Proc. Cambridge Philos. Soc. 152, 473–496.CrossRefGoogle Scholar
Smith, D. A. (2015) The Unified Transform Method for Linear Initial-Boundary Value Problems: A Spectral Interpretation, Unified Transform Method for Boundary Value Problems: Applications and Advances, SIAM, Philadelphia, PA.Google Scholar
Smith, D. A., Trogdon, T. & Vasan, V. (2019) Linear dispersive shocks, (submitted) arXiv:1908.08716 [math.AP].Google Scholar
Stadler, W. (1973) A theorem on the uniform convergence of Fourier-type integrals. J. Math. Anal. Appl. 42, 409–412.CrossRefGoogle Scholar
Usero, D. (2008) Fractional Taylor series for Caputo fractional derivatives. Construction of numerical schemes. http://www.fdi.ucm.es/profesor/lvazquez/calcfrac/docs/paper_Usero.pdf,.Google Scholar
Wang, L., Yang, Bi ., Yu, X. & Zeng, C. (2017) Identification of the boundary heat transfer coefficient from interior measurement of temperature field. Appl. Math. Lett. 63, 6–13.CrossRefGoogle Scholar