2 Adversarial robustness and its Bayesian relaxation

In the following, we consider a supervised machine learning problem of the following form. We are given a training dataset $\{(y_1, z_1),\ldots, (y_K, z_K)\}$ of pairs of features $y_1,\ldots, y_K \in Y \,:\!=\,\mathbb {R}^{d_Y}$ and labels $z_1,\ldots, z_K \in Z$ . Moreover, we are given a parametric model of the form $g: X \times Y \rightarrow Z$ , with $X \,:\!=\, \mathbb {R}^d$ denoting the parameter space. The goal is now to find a parameter $\theta ^*$ , for which

\begin{equation*} g(y_k|\theta ^*) \approx z_k \qquad (k=1,\ldots, K). \end{equation*}

In practice the function $g(\!\cdot |\theta ^*)$ shall then be used to predict labels of features (especially such outside of training dataset).

The parameter $\theta ^*$ is usually found through optimisation. Let $\mathcal {L}:Z \times Z \rightarrow \mathbb {R}$ denote a loss function – a function that gives a reasonable way of comparing the output of $g$ with observed labels. Usual examples are the square loss for continuous labels and cross entropy loss for discrete labels. Then, we need to solve the following optimisation problem:

(2.1) \begin{align} \min _{\theta \in X} & \frac {1}{K}\sum _{k=1}^K \Phi (y_k,z_k|\theta ), \end{align}

where $\Phi (y,z|\theta ) \,:\!=\, \mathcal {L}(g(y|\theta ),z)$ .

Machine learning models $g$ that are trained in this form are often susceptible to adversarial attacks. That means, for a given feature vector $y$ , we can find a ‘small’ $\xi \in Y$ for which $g(y+\xi |\theta ^*) \neq g(y|\theta ^*)$ . In this case, an adversary can change the model’s predicted label by a very slight alteration of the input feature. Such a $\xi$ can usually be found through optimisation on the input domain:

\begin{equation*}\max _{\xi \in B(\varepsilon )}\Phi (y+\xi, z|\theta ),\end{equation*}

where $B(\varepsilon ) = \{\xi : \|\xi \|\leq \varepsilon \}$ denotes the $\varepsilon$ -ball centred at $0$ and $\varepsilon \gt 0$ denotes the size of the adversarial attack. Hence, the attacker tries to change the prediction of the model whilst altering the model input only by a small value $\leq \varepsilon$ . Other kinds of attacks are possible, the attacker may, e.g. try to not only change the predicted label to any other label, but rather to a particular target label, see, e.g. [Reference Kurakin, Goodfellow and Bengio26].

In adversarially robust training, we replace the optimisation problem (2.1) by the minmax optimisation problem below:

(2.2) \begin{equation} \min _{\theta \in X} \frac {1}{K}\sum _{k=1}^K \max _{\xi _k \in B(\varepsilon )}\Phi (y_k+\xi _k,z_k|\theta ). \end{equation}

Thus, we now train the network by minimising the loss also with respect to potential adversarial attacks. Finding the accurate solutions to such minmax optimisation problems is difficult: usually there is no underlying saddlepoint structure, e.g. $\Phi (y,z|\theta )$ is neither convex in $\theta$ nor concave in $y$ , $X$ and $Y$ tend to be very high-dimensional spaces, and the number of data points $K$ may prevent the accurate computation of gradients. However, good heuristics have been established throughout the last decade – we have mentioned some of them in Section 1.

In this work, we aim to study a relaxed version of the minmax problem, which we refer to as the Bayesian adversarial robustness problem. This problem is given by

(2.3) \begin{equation} \min _{\theta \in X} \frac {1}{K}\sum _{k =1}^K \int _{B({\varepsilon })} \Phi (y_k+\xi _k,z_k|\theta ) \pi ^{\gamma, \varepsilon }_k(\mathrm {d}\xi _k|\theta ), \end{equation}

where the Bayesian adversarial distribution $\pi ^{\gamma, \varepsilon }_k(\cdot |\theta )$ has (Lebesgue) density

\begin{equation*} \xi \mapsto \frac {\exp (\gamma \Phi (y_k+\xi, z_k|\theta )) \mathbf {1}[\xi \in B(\varepsilon )]}{\int _{B(\varepsilon )} \exp (\gamma \Phi (y_k+\xi ',z_k|\theta )) \mathrm {d}\xi '}, \end{equation*}

where $\gamma \gt 0$ is an inverse temperature, $\varepsilon \gt 0$ still denotes the size of the adversarial attack, and $\mathbf {1}[\cdot ]$ denotes the indicator: $\mathbf {1}[\mathrm {true}] \,:\!=\, 1$ and $\mathbf {1}[\mathrm {false}] \,:\!=\, 0$ . The distribution $\pi ^{\gamma, \varepsilon }_k(\cdot |\theta )$ is concentrated on the $\varepsilon$ -ball, $\varepsilon \gt 0$ controls the range of the attack, $\gamma \gt 0$ controls its focus. We illustrate this behaviour in Figure 1. Next, we comment on the mentioned relaxation and the Bayesian derivation of this optimisation problem.

Figure 1. Plots of the Lebesgue density of $\pi _1^{\gamma, \varepsilon }(\cdot |\theta _0)$ for energy $\Phi (y_1 + \xi, z_1|\theta _0) = (\xi -0.1)^2/2$ , choosing parameters $\varepsilon \in \{0.025, 0.1, 0.4\}$ and $\gamma \in \{0.1, 10, 1000\}$ .

2.1 Relaxation

Under certain assumptions,Footnote ¹ one can show that

\begin{equation*}\pi ^{\gamma, \varepsilon }_k(\cdot |\theta ) \rightarrow \mathrm {Unif}(\mathrm {argmax}_{\xi \in Y} \Phi (y_k + \xi, z_k|\theta ))\end{equation*}

weakly as $\gamma \rightarrow \infty$ , see [Reference Hwang20]. Indeed, the Bayesian adversarial distribution converges to the uniform distribution over the global maximisers computed with respect to the adversarial attack. This limiting behaviour, that we can also see in Figure 1, forms the basis of simulated annealing methods for global optimisation. Moreover, it implies that the optimisation problems (2.2) and (2.3) are identical in the limit $\gamma \to \infty$ , since

\begin{align*} \lim _{\gamma \rightarrow \infty } \frac {1}{K}\sum _{k =1}^K &\int _{B({\varepsilon })} \Phi (y_k+\xi _k,z_k|\theta ) \pi ^{\gamma, \varepsilon }_k(\mathrm {d}\xi _i|\theta ) \\ &= \frac {1}{K}\sum _{k =1}^K \int _{B({\varepsilon })} \Phi (y_k+\xi _k,z_k|\theta ) \mathrm {Unif}(\mathrm {argmax}_{\xi \in Y} \Phi (y_k + \xi, z_k|\theta ))(\mathrm {d}\xi _i), \end{align*}

and since $\xi _k \sim \mathrm {Unif}(\mathrm {argmax}_{\xi \in Y} \Phi (y_k + \xi, z_k|\theta ))$ implies $\Phi (y_k+\xi _k,z_k|\theta ) = \max _{\xi \in B(\varepsilon )}\Phi (y_k+\xi, z_k|\theta )$ almost surely for $k =1,\ldots, K$ . A strictly positive $\gamma$ on the other hand leads to a relaxed problem circumventing the minmax optimisation. [Reference Cipriani, Scagliotti and Wöhrer8] have also discussed this relaxation of an adversarial robustness problem in the context of a finite set of attacks, i.e. the $\varepsilon$ -ball $B(\varepsilon )$ is replaced by a finite set. Probabilistically robust learning is another type of relaxation, see for example [Reference Bungert, Trillos, Jacobs, McKenzie, Nikolić and Wang4, Reference Robey, Chamon, Pappas and Hassani43]. Similar to our work, instead of doing the worst-case optimisation, i.e. finding the perturbation $\xi$ that maximises the loss, they replace it with a probability measure on $\xi$ . This probability measure, however, follows a different paradigm.

2.2 Bayesian attackers

We can understand the kind of attack that is implicitly employed in (2.3) as a Bayesian attack. We now briefly introduce the Bayesian learning problem to then explain its relation to this adversarial attack. In Bayesian learning, we model $\theta$ as a random variable with a so-called prior (distribution) $\pi _{\textrm { prior}}$ . The prior incorporates information about $\theta$ . In Bayesian learning, we now inform the prior about data $\{(y_1, z_1),\ldots, (y_K, z_K)\}$ by conditioning $\theta$ on that data. Indeed, we train the model by finding the conditional distribution of $\theta$ given that $g(y_k|\theta ) \approx z_k$ ( $k =1,\ldots, K)$ . In the Bayesian setting, we represent ‘ $\approx$ ’ by a noise assumption consistent with the loss function $\mathcal {L}$ . This is achieved by defining the so-called likelihood as $\exp (\!-\Phi )$ . The conditional distribution describing $\theta$ is called the posterior (distribution) $\pi _{\textrm { post}}$ and can be obtained through Bayes’ theorem, which states that

\begin{equation*} \pi _{\textrm { post}}(A) = \frac {\int _A \exp \left (-\frac {1}{K}\sum _{k=1}^K\Phi (y_k, z_k|\theta )\right ) \pi _{\textrm { prior}}(\mathrm {d}\theta )}{\int _X \exp \left (-\frac {1}{K}\sum _{i=k}^K\Phi (y_k, z_k|\theta )\right ) \pi _{\textrm { prior}}(\mathrm {d}\theta )}, \end{equation*}

for measurable $A \subseteq X$ . A model prediction with respect to feature $y$ can then be given by the posterior mean of the output $g$ , which is

\begin{equation*} \int _{{\mathbb {R}}^n} g(y|\theta ) \pi _{\textrm { post}}(\mathrm {d}\theta ). \end{equation*}

The Bayesian attacker treats the attack $\xi _k$ in exactly such a Bayesian way. They define a prior distribution for the attack, which is the uniform distribution over the $\varepsilon$ -ball:

\begin{equation*}\mathrm {Unif}(B(\varepsilon )) = \int _{B(\varepsilon )}\mathbf {1}[\xi _k \in \cdot ]\mathrm {d}\xi _k.\end{equation*}

The adversarial likelihood is designed to essentially cancel out the likelihood in the Bayesian learning problem, by defining a function that gives small mass to the learnt prediction and large mass to anything that does not agree with the learnt prediction:

\begin{equation*} \exp (\gamma \Phi (y_k+\xi _k,z_k|\theta )). \end{equation*}

Whilst this is not a usual likelihood corresponding to a particular noise model, we could see this as a special case of Bayesian forgetting [Reference Fu, He, Xu and Tao12]. In Bayesian forgetting, we would try to remove a single dataset from a posterior distribution by altering the distribution of the parameter $\theta$ . In this case, we try to alter the knowledge we could have gained about the feature vector by altering that feature vector to produce a different prediction.

3 Adversarial Bayesian particle sampler

We now derive a particle-based method that shall solve (2.3). To simplify the presentation in the following, we assume that $K=1$ , i.e. there is only a single data point. The derivation for multiple data points is equivalent – computational implications given by multiple data points will be discussed in Section 6. We also ignore the dependence of $\Phi$ on particular data points and note only the dependence on parameter and attack. Indeed, we write (2.3) now as

\begin{equation*} \min _{\theta \in X} F(\theta ) \,:\!=\, \int _{B({\varepsilon })} \Phi (\xi, \theta ) \pi ^{\gamma, \varepsilon }(\mathrm {d}\xi |\theta ). \end{equation*}

To solve this minimisation problem, we study the gradient flow corresponding to the energy $F$ , that is: ${\mathrm {d}\zeta _t} = -\nabla _\zeta F(\zeta _t){\mathrm {d}t}$ . The gradient flow is a continuous-time variant of the gradient descent algorithm. The gradient flow can be shown to converge to a minimiser of $F$ in the longterm limit if $F$ satisfies certain regularity assumptions. The gradient of $F$ has a rather simple expression:

\begin{align*} \nabla _\theta F(\theta ) &= \nabla _\theta \frac { \int _{B(\varepsilon )}\Phi (\xi, \theta )\exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi }{\int _{B(\varepsilon )} \exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi } \\ &= \frac { \int _{B(\varepsilon )} \nabla _\theta \Phi (\xi, \theta ) \cdot \exp (\gamma \Phi (\xi, \theta )) + \gamma \nabla _\theta \Phi (\xi, \theta ) \cdot \Phi (\xi, \theta )\exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi }{\int _{B(\varepsilon )} \exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi } \\ &\qquad - \frac {\left ( \int _{B(\varepsilon )}\Phi (\xi, \theta )\exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi \right )\left (\int _{B(\varepsilon )} \gamma \nabla _\theta \Phi (\xi, \theta ) \cdot \exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi \right )}{\left (\int _{B(\varepsilon )}\exp (\gamma \Phi (\xi, \theta )) \mathrm {d}\xi \right )^2} \\ &= \int _{B({\varepsilon })} \nabla _\theta \Phi (\xi, \theta ) \pi ^{\gamma, \varepsilon }(\mathrm {d}\xi |\theta ) + \gamma \mathrm {Cov}_{\pi ^{\gamma, \varepsilon }(\cdot |\theta )}(\Phi (\cdot, \theta ), \nabla _\theta \Phi (\cdot, \theta )), \end{align*}

where we assume that $\Phi$ is continuously differentiable, bounded below and sufficiently regular to be allowed here to switch gradients and integrals. As usual, we define the covariance of appropriate functions $f,g$ with respect to a probability distribution $\pi$ , by

\begin{equation*} \mathrm {Cov}_{\pi }(f,g) \,:\!=\, \int _X f(\theta )g(\theta ) \pi (\mathrm {d}\theta ) - \int _X f(\theta ) \pi (\mathrm {d}\theta )\int _X g(\theta ) \pi (\mathrm {d}\theta ). \end{equation*}

The structure of $\nabla _\theta F$ is surprisingly simple, requiring only integrals of the target function and its gradient with respect to $\pi ^{\gamma, \varepsilon }$ , but, e.g. not its normalising constant. In practice, it is usually not possible to compute these integrals analytically or to even sample independently from $\pi ^{\gamma, \varepsilon }(\cdot |\theta )$ , which would be necessary for a stochastic gradient descent approach. The latter approach first introduced by [Reference Robbins and Monro42] allows the minimisation of expected values by replacing these expected values by sample means; see also [Reference Jin, Latz, Liu and Schönlieb22] and [Reference Latz28] for continuous-time variants. Instead, we use a particle system approach that has been studied for a different problem by [Reference Johnston, Crucinio, Akyildiz, Sabanis and Girolami2] and [Reference Kuntz, Lim and Johansen24]. The underlying idea is to approximate $\pi ^{\gamma, \varepsilon }(\cdot |\theta )$ by an overdamped Langevin dynamics, which is restricted to the $\varepsilon$ -Ball $B(\varepsilon )$ with reflecting boundary conditions:

\begin{equation*}\mathrm {d}\xi _t = \gamma \nabla _\xi \Phi (\xi _t,\theta )\mathrm {d}t + \sqrt {2}\mathrm {d}W_t,\end{equation*}

where $(W_t)_{t \geq 0}$ denotes a standard Brownian motion on $Y$ . Alternatively, one may write the dynamics as $\mathrm {d}\xi _t = \nabla _\xi \Phi (\xi _t,\theta )\mathrm {d}t + \sqrt {2/\gamma }\mathrm {d}W_t$ , which is equivalent to the current form after a time re-scaling. Under weak assumptions on $\Phi$ , this Langevin dynamics converges to the distribution $\pi ^{\gamma, \varepsilon }(\cdot |\theta )$ as $t \rightarrow \infty$ . However, due to the heavy computational costs, in practice, we are not able to simulate the longterm behaviour of this dynamics for all fixed $\theta$ to produce samples of $\pi ^{\gamma, \varepsilon }(\cdot |\theta )$ as required for stochastic gradient descent. Instead, we run a number $N$ of (seemingly independent) Langevin dynamics $(\xi _t^{1,N})_{t \geq 0}, \ldots, (\xi _t^{N,N})_{t \geq 0}$ . We then obtain an approximate gradient flow $(\theta _t^N)_{t \geq 0}$ that uses the ensemble of particles $(\xi _t^{1,N})_{t \geq 0}, \ldots, (\xi _t^{N,N})_{t \geq 0}$ to approximate the expected values in the gradient $\nabla _\theta F$ and then feed $(\theta _t^N)_{t \geq 0}$ back into the drift of the $(\xi _t^{1,N})_{t \geq 0}, \ldots, (\xi _t^{N,N})_{t \geq 0}$ . Hence, we simultaneously approximate the gradient flow $(\zeta _t)_{t \geq 0}$ by $(\theta ^N_t)_{t \geq 0}$ and the Bayesian adversarial distribution $(\pi ^{\gamma, \varepsilon }(\cdot |\theta ^N_t))_{t \geq 0}$ by $(\xi _t^{1,N})_{t \geq 0}, \ldots, (\xi _t^{N,N})_{t \geq 0}$ . Overall, we obtain the dynamical system

\begin{align*} \mathrm {d}\theta _t^N &= - \frac {1}{N}\sum _{n=1}^N\nabla _\theta \Phi (\xi _t^{n,N},\theta _t^N)\mathrm {d}t - \gamma \widehat {\mathrm {Cov}}(\xi _t^N)\mathrm {d}t, \\ \mathrm {d}\xi _t^{i,N} &= \gamma \nabla _\xi \Phi (\xi _t^{i,N},\theta ^N_t)\mathrm {d}t + \sqrt {2}\mathrm {d}W_t^{i} \qquad (i =1,\ldots, N). \end{align*}

where $(W_t^{i})_{t \geq 0}$ are mutually independent Brownian motions on $Y$ for $i = 1,\ldots, N$ . Again, the Langevin dynamics $(\xi _t^{1,N})_{t \geq 0}, \ldots, (\xi _t^{N,N})_{t \geq 0}$ are defined on the ball $B(\varepsilon )$ with reflecting boundary conditions – we formalise this fact below. The empirical covariance is given by

\begin{equation*}\widehat {\mathrm {Cov}}(\xi _t^N) = \frac 1{N} \sum _{i=1}^N \Phi (\xi _t^{i,N},\theta ^N_t)\nabla _\theta \Phi (\xi _t^{i,N},\theta ^N_t) - \frac 1{N^2}\sum _{i=1}^K \Phi (\xi _t^{i,N},\theta ^N_t) \sum _{j=1}^K\nabla _\theta \Phi (\xi _t^{j,N},\theta ^N_t).\end{equation*}

We refer to the dynamical system $(\theta ^N_t, \xi ^{1,N}_t,\ldots, \xi ^{N,N}_t)_{t \geq 0}$ as Abram. We illustrate the dynamics of Abram in Figure 2, where we consider a simple example.

Figure 2. Examples of the Abram method given $\Phi (\xi, \theta ) = \frac {1}{2}(\xi + \theta )^2$ , $\varepsilon = 1$ , and different combinations of $(\gamma, N) = (10,3)$ (top left), $(0.1,3)$ (top right), $(10,50)$ (bottom left), $(0.1, 50)$ (bottom right). In each of the four quadrants, we show the simulated path $(\theta _t^N)_{t \geq 0}$ (top), the particle paths $(\xi _t^{1,N},\ldots, \xi _t^{N,N})_{t \geq 0}$ (centre), and the path of probability distributions $(\pi ^{\gamma, \varepsilon }(\cdot |\theta _t^N))_{t \geq 0}$ (bottom) that shall be approximated by the particles. The larger $\gamma$ leads to a concentration of $\pi ^{\gamma, \varepsilon }$ at the boundary, whilst it is closer to uniform if $\gamma$ is small. More particles lead to a more stable path $(\theta ^N_t)_{t \geq 0}$ . A combination of large $N$ and $\gamma$ leads to convergence to the minimiser $\theta _* = 0$ of $F$ .

We have motivated this particle system as an approximation to the underlying gradient flow $(\zeta _t)_{t \geq 0}$ . As $N \rightarrow \infty$ , the dynamics $(\theta ^N_t)_{t \geq 0}$ does not necessarily convergence to the gradient flow $(\zeta _t)_{t \geq 0}$ , but to a certain McKean–Vlasov stochastic differential equation (SDE), see [Reference McKean34]. We study this convergence behaviour in the following, as well as the convergence of the McKean–Vlasov SDE to the minimiser of $F$ and, thus, justify Abram as a method for Bayesian adversarial learning. First, we introduce the complete mathematical set-up and give required assumptions. To make it easier for the reader to keep track of the different stochastic processes that appear throughout this work, we summarise them in Table 1.

Table 1. Definitions of stochastic processes throughout this work

3.1 Mean-field limit

In the following, we are interested in the mean field limit of Abram, i.e. we analyse the limit of $(\theta ^N_t)_{t \geq 0}$ as $N \rightarrow \infty$ . Thus, we can certainly assume for now that $\gamma \,:\!=\, 1$ and $\varepsilon \in (0,1)$ being fixed. We write $B \,:\!=\, B(\varepsilon )$ . Then, Abram $(\theta ^N_t, \xi ^{1,N}_t,\ldots, \xi ^{N,N}_t)_{t \geq 0}$ satisfies

(3.1) \begin{align} \theta ^N_t &= \theta _0 - \int _0^t\mu _s^N(\nabla _\theta \Phi (\cdot, \theta ^N_s))\mathrm {d}s - \int _0^t \mathrm {Cov}_{\mu _s^N}(\Phi (\cdot, \theta ^N_s),\nabla _\theta \Phi (\cdot, \theta ^N_s))\mathrm {d}s, \\ \xi _t^{i,N} &=\xi ^i_0 +\int _0^t\nabla _x \Phi (\xi _s^{i,N},\theta ^N_s)\mathrm {d}s + \sqrt {2}W^i_t+\int _0^tn(\xi _s^{i,N})\mathrm {d}l^{i,N}_s\qquad (i=1,\ldots, N). \nonumber \end{align}

Here, $(W_t^1)_{t \geq 0},\ldots, (W_t^N)_{t \geq 0}$ are independent Brownian motions on $Y$ and the initial particle values $\xi ^1_0,\ldots, \xi ^N_0$ are independent and identically distributed. There and throughout the rest of this work, we denote the expectation of some appropriate function $f$ with respect to a probability measure $\pi$ by $\pi (f) \,:\!=\, \int _X f(\theta ) \pi (\mathrm {d}\theta ).$ We use $\mu _t^N$ to denote the empirical distribution of the particles $(\xi _t^{1,N}, \ldots, \xi _t^{N,N})$ at time $t \geq 0$ . That is $\mu _t^N\,:\!=\,\frac {1}{N}\sum _{i=1}^N\delta (\!\cdot - {\xi _t^{i, N}})$ , where $\delta (\!\cdot - \xi )$ is the Dirac mass concentrated in $\xi \in B$ . This implies especially that we can write

\begin{align*} \mu _t^N(f) = \frac {1}{N}\sum _{i=1}^N f(\xi _t^{i,N}), \qquad \mathrm {Cov}_{\mu _t^N}(f,g) = \frac {1}{N}\sum _{i=1}^N f(\xi _t^{i,N})g(\xi _t^{i,N})-\frac {1}{N^2}\sum _{i=1}^N \sum _{j=1}^N f(\xi _t^{i,N})g(\xi _t^{j,N}), \end{align*}

for appropriate functions $f$ and $g$ . The particles are constrained to stay within $B$ by the last term in the equations of the $(\xi _t^{1,N}, \ldots, \xi _t^{N,N})_{t \geq 0}$ . Here, $n(x)=-x/\left \|x \right \|$ for $x\in \partial B$ is the inner normal vector field. Although we focus on Abram $(\theta ^N_t, \xi ^{1,N}_t,\ldots, \xi ^{N,N}_t)_{t \geq 0}$ , we remark that the solution of equations (3.1) is $(\theta ^N_t, \xi ^{1,N}_t,\ldots, \xi ^{N,N}_t, l^{1,N}_t,\ldots, l^{N,N}_t)_{t \geq 0}$ . The functions $(l^{1,N}_t,\ldots, l^{N,N}_t)_{t \geq 0}$ are uniquely defined under the additional conditions:

1. (1) $l^{i,N}$ ’s are non-decreasing with $l^{i,N}(0)=0$ and

2. (2) $\int _0^t \boldsymbol {1}[{\xi ^{i,N}_s\notin \partial B(\varepsilon )}]dl^{i,N}(s)=0$ .

Condition (2) implies that $l^{i,N}$ can increase only when $\xi ^{i, N}$ is in $\partial B(\varepsilon )$ . Intuitively, $l^{i,N}$ cancels out part of $\xi ^{i, N}$ so that it stays inside $B(\varepsilon )$ . For more discussion on diffusion processes with reflecting boundary conditions, see e.g. [Reference Pilipenko40]. Additionally, it is convenient to define

\begin{align*} G(\theta, \nu )= \nabla _\theta \Big [\nu ( \Phi (\cdot, \theta ))+ \mathrm {Var}_\nu [\Phi (\cdot, \theta )]/2\Big ]=\nu (\nabla _\theta \Phi (\cdot, \theta ))+\mathrm {Cov}_{\nu }(\Phi (\cdot, \theta ),\nabla _\theta \Phi (\cdot, \theta )), \end{align*}

for any probability measure $\nu$ on $({B}, \mathcal {B}B)$ and $\theta \in X$ , where $\mathcal {B}B$ denotes the Borel- $\sigma$ -algebra corresponding to $B$ and, following the notation above, $\nu ( \Phi (\cdot, \theta )) = \int _B \Phi (\xi, \theta )\nu (\mathrm {d}\xi )$ . We finish this background section by defining the limiting McKean–Vlasov SDE with reflection

(3.2) \begin{align} \theta _t &= \theta _0- \int _0^t\mu _s(\nabla _\theta \Phi (\cdot, \theta _s))\mathrm {d}s - \int _0^t \mathrm {Cov}_{\mu _s}(\Phi (\cdot, \theta _s),\nabla _\theta \Phi (\cdot, \theta _s))\mathrm {d}s,\\ \xi _t &=\xi _0+ \int _0^t\nabla _x \Phi (\xi _s,\theta _s)\mathrm {d}s + \sqrt {2}W_t+\int _0^tn(\xi _s)\mathrm {d}l_s, \nonumber \end{align}

with $\mu _t$ denoting the law of $\xi _t$ at time $t \geq 0$ . The goal of this work is to show that the particle system (3.1) converges to this McKean–Vlasov SDEs as $N\to \infty$ and to then show that the McKean–Vlasov SDE can find the minimiser of $F$ .

3.2 Assumptions

We now list assumptions that we consider throughout this work. We start with the Lipschitz continuity of $\nabla \Phi$ and $G$ .

Assumption 3.1 (Lipschitz). The function $\nabla _\xi \Phi$ is Lipschitz continuous, i.e. there exists a Lipschitz constant $L\gt 1$ such that

\begin{align*} \left \|\nabla _\xi \Phi (\xi, \tilde \theta )-\nabla _\xi \Phi (\tilde \xi, \tilde \theta ) \right \|\le L\Big (\left \|\xi -\tilde \xi \right \|+\left \|\theta -\tilde \theta \right \|\Big ), \end{align*}

for any $\xi, \tilde \xi \in B$ and $\theta, \tilde \theta \in {\mathbb {R}}^n$ . Similarly, we assume that $G(\theta, \mu )$ is Lipschitz in the following sense: there is an $L\gt 1$ such that

\begin{align*} \left \|G(\theta, \nu )-G(\tilde \theta, \tilde \nu ) \right \|\le L\Big (\left \|\theta -\tilde \theta \right \|+{{\mathcal W}}_1(\nu, \tilde \nu )\Big ), \end{align*}

for any probability measures $\nu$ , $\tilde \nu$ on $(B, \mathcal {B}B)$ and $\theta, \ \tilde \theta \in {\mathbb {R}}^n.$

In Assumption 3.1 and throughout this work, ${{\mathcal W}}_p$ denotes the Wasserstein- $p$ distance given by

\begin{align*} {{\mathcal W}}^p_p(\nu, \nu ') = \inf \left \lbrace \int _{X\times X}\left \|y-y' \right \|^p\Gamma (\mathrm {d}y,\mathrm {d}y') : \Gamma \text { is a coupling of } \nu, \nu '\right \rbrace, \end{align*}

for probability distributions $\nu, \nu '$ on $(X, \mathcal {B}X)$ and $p \geq 1$ . In addition to the Wasserstein distance, we sometimes measure the distance between probability distributions $\nu, \nu '$ on $(X, \mathcal {B}X)$ using the total variation distance given by

\begin{equation*} \|\nu -\nu '\|_{{\textrm { TV}}} = \sup _{A \in \mathcal {B}X}|\nu (A)-\nu '(A)|. \end{equation*}

The Lipschitz continuity of $G$ actually already implies the Lipschitz continuity of $\nabla _\theta \Phi$ . By setting $\nu = \delta (\cdot -\xi )$ and $\tilde \nu =\delta (\cdot - {\tilde \xi })$ , we have

\begin{align*} \left \|\nabla _\theta \Phi (\xi, \tilde \theta )-\nabla _\theta \Phi (\tilde \xi, \tilde \theta ) \right \| &= \left \|G(\theta, \delta (\cdot -\xi ))-G(\tilde \theta, \delta (\cdot -\tilde \xi )) \right \| \\ &\le L\Big (\left \|\theta -\tilde \theta \right \|+{{\mathcal W}}_1(\delta (\cdot - \xi ),\delta (\cdot - \tilde \xi ))\Big ) = L\Big (\left \|\xi -\tilde \xi \right \|+\left \|\theta -\tilde \theta \right \|\Big ) . \end{align*}

We assume throughout that the constant $L\gt 1$ to simplify the constants in the Theorem5.5. Finally, we note that Assumption 3.1 implies the well-posedness of both (3.1) and (3.2), see ([Reference Adams, dos Reis, Ravaille, Salkeld and Tugaut1], Theorems 3.1, 3.2).

Next, we assume the strong monotonicity of $G$ , which, as we note below, also implies the strong convexity of $\Phi (x,\cdot )$ for any $x \in B$ . This assumption is not realistic in the context of deep learning (e.g. [Reference Choromanska, Henaff, Mathieu, Arous and LeCun7]), but not unusual when analysing learning techniques.

Assumption 3.2 (Strong monotonicity). For any probability measure $\nu$ on $(B, \mathcal {B}B)$ , $G(\cdot, \nu )$ is $2\lambda$ -strongly monotone, i.e. for any $\theta, \tilde \theta \in {\mathbb {R}}^n$ , we have

\begin{align*} \left \langle G(\theta, \nu )-G(\tilde \theta, \nu ), \theta -\tilde \theta \right \rangle \ge 2\lambda \left \|\theta -\tilde \theta \right \|^2, \end{align*}

for some $\lambda \gt 0$ .

By choosing $\nu = \delta (\cdot -\xi )$ in Assumption 3.2 for $\xi \in B,$ we have $\mathrm {Cov}_{\nu }(\Phi (\cdot, \theta ),\nabla _\theta \Phi (\cdot, \theta ))=0$ , which implies that $\left \langle \nabla _\theta \Phi (x,\theta ) -\nabla _\theta \Phi (x,\theta '),\theta -\theta '\right \rangle \ge 2\lambda \left \|\theta -\theta ' \right \|^2$ . Thus, the $2\lambda$ -strong monotonicity of $G$ in $\theta$ also implies the $2\lambda$ -strong convexity of $\Phi$ in $\theta$ .

The assumptions stated throughout this sections are fairly strong, they are satisfied in certain linear-quadratic problems on bounded domains. We illustrate this in an example below.

Example 3.3. We consider a prototypical adversarial robustness problem based on the potential $\Phi (\xi, \theta ) \,:\!=\, \left \|\xi -\theta \right \|^2$ with $\theta$ in a bounded set $X' \subseteq X$ – problems of this form appear, e.g. in adversarially robust linear regression. Next, we are going to verify that this problem satisfies Assumptions 3.1 and 3.2 .

We have $\nabla _\xi \Phi (\xi, \theta )=2(\xi -\theta ),$ which is Lipschitz in both $\theta$ and $\xi$ . Since

\begin{align*} \nabla _\theta \Phi (\xi, \theta )&=2(\xi -\theta ), \\ \Phi (\xi, \theta )-\int _B\Phi (\xi, \theta )\nu (\mathrm d \xi )&=\left (\left \|\xi \right \|^2-\int _B \left \|\xi \right \|^2\nu (\mathrm d \xi )\right ) -2\theta \cdot \left (\xi -\int _B \xi \nu (\mathrm d \xi )\right ), \\ \nabla _\theta \Phi (\xi, \theta )-\int _B\nabla _\theta \Phi (\xi, \theta )\nu (\mathrm d \xi ) &=-2\left (\xi -\int _B \xi \nu (\mathrm d \xi )\right ), \end{align*}

we have that

\begin{align*} G(\theta, \nu )= 2\theta -2{\mathbb E}_\nu [\xi ]+4\theta \cdot \mathrm {Var}_\nu (\xi )-2 \mathrm {Cov}_\nu (\left \|\xi \right \|^2,\xi ), \end{align*}

where ${\mathbb E}_\nu [\xi ]=\int _B \xi \nu (\mathrm d \xi )$ and $\mathrm {Cov}_\nu (\left \|\xi \right \|^2,\xi )= \int _B(\left \|\xi \right \|^2-{\mathbb E}_\nu [\left \|\xi \right \|^2]) (\xi -{\mathbb E}_\nu [\xi ])\nu (\mathrm d \xi )$ . Since the $\varepsilon$ -ball and $\theta \in X'$ are bounded, we have that $G(\theta, \nu )$ is Lipschitz in both $\theta$ and $\nu$ . Thus, it satisfies Assumption 3.1 . In order to make $G(\theta, \nu )$ satisfy Assumption 3.2 , we choose $\varepsilon$ small enough such that the term $4\theta \cdot \mathrm {Var}_\nu (\xi )$ is $1$ -Lipschitz. In this case, we can verify that $\left \langle G(\theta, \nu )-G(\theta ',\nu ),\theta -\theta '\right \rangle \ge \left \|\theta -\theta ' \right \|^2$ and, thus, Assumption 3.2 .

4 Propagation of chaos

We now study the large particle limit ( $N\to \infty$ ) of the Abram dynamics (3.1). When considering a finite time interval $[0,T]$ , we see that the particle system (3.1) approximates the McKean–Vlasov SDE (3.2) in this limit. We note that we assume in the following that $0\lt \varepsilon \lt 1$ . Moreover, we use the Wasserstein- $2$ distance instead of Wasserstein- $1$ distance in Assumption 3.1. We have ${{\mathcal W}}_1(\nu, \nu ')\le {{\mathcal W}}_2(\nu, \nu ')$ for any probability measures $\nu, \nu '$ for which the distances are finite, see [Reference Villani52]. Thus, convergence in ${{\mathcal W}}_2$ also implies convergence in ${{\mathcal W}}_1$ . We now state the main convergence result.

Theorem 4.1. Let Assumption 3.1 hold. Then, there is a constant $C_{d,T}\gt 0$ such that for all $T\ge 0$ and $N\ge 1$ we have the following inequality

\begin{align*} \sup _{t\in [0,T]}{\mathbb E}\big [\left \|\theta _t^N-\theta _t \right \|^2+{{\mathcal W}}^2_2(\mu _t^N,\mu _t)\big ]\le o_{d,T,N}\,:\!=\,C_{d,T} {\begin{cases} N^{-\alpha _d},&\text { if } d\ne 4,\\ \log (1+N)N^{-\frac {1}{2}},&\text { if }d=4, \end{cases} } \end{align*}

where $\alpha _d= 2/d$ for $d\gt 4$ and $\alpha _d=1/2$ for $d\lt 4.$

The dependence of $d, T$ on $C_{d, T}$ is not explicit except in some special cases which we discuss in Section 5. The upper bound is essentially $N^{-2/d}+N^{-1/2}$ with the dominating term differing for $d\gt 4$ and $d\lt 4$ . In fact, when $d\lt 4$ , the convergence rate can not be better than $N^{-1/2},$ see ( [Reference Fournier and Guillin11], Page 2) for an example in which the lower bound is obtained.

Hence, we obtain convergence of both the gradient flow approximation $(\theta ^N_t)_{t \geq 0}$ and the particle approximation $(\mu _t^N)$ to the respective components in the McKean–Vlasov SDE. We prove this result by a coupling method. To this end, we first collect a few auxiliary results: studying the large sample limit of an auxiliary particle system and the distance of the original particle system to the auxiliary system. To this end, we sample $N$ trajectories of $(\xi _t)_{t \geq 0}$ from equations (3.2) as

(4.1) \begin{align} \xi ^i_t &=\xi ^i_0+ \int _0^t\nabla _x \Phi (\xi ^i_s,\theta _s)\mathrm {d}s + \sqrt {2}W^i_t+\int _0^tn(\xi ^i_s)\mathrm {d}l^i_s \qquad (i=1, \ldots, N), \end{align}

where the Brownian motions $(W_t^1,\ldots, W_t^N)_{t \geq 0}$ are the ones from (3.1). Of course these sample paths $(\xi _t^1,\ldots, \xi _t^N)_{t \geq 0}$ are different from the $(\xi _t^{1,N},\ldots, \xi _t^{N,N})_{t \geq 0}$ in equation (3.1): Here, $(\theta _t)_{t \geq 0}$ only depends on the law of $(\xi _t)_{t \geq 0}$ , whereas $(\theta _t^N)_{t \geq 0}$ depends on position of the particles $(\xi ^{i,N}_t)_{t \geq 0}$ . As the $(\xi _t^1)_{t \geq 0}, \ldots, (\xi _t^N)_{t \geq 0}$ are i.i.d., we can apply the empirical law of large numbers from [Reference Fournier and Guillin11] and get the following result.

Proposition 4.2. Let Assumption 3.1 hold. Then,

\begin{equation*}\sup _{t\ge 0}{\mathbb E}\Big [ {{\mathcal W}}^2_2\Big (N^{-1}\sum ^N_{i=1}\delta _{\xi _t^i},\mu _t\Big )\Big ]\le o_{d,T,N},\end{equation*}

where $o_{d,T,N}$ is the constant given in Theorem 4.1 .

For any $i = 1,\ldots, N$ , we are now computing bounds for the pairwise distances between $\xi ^i_t$ and $\xi _t^{i,N}$ for $t \geq 0$ . We note again that these paths are pairwise coupled through the associated Brownian motions $(W_t^i)_{t \geq 0}$ , respectively.

Lemma 4.3. Let Assumption 3.1 hold and recall that $\xi _0^{i,N} = \xi _0^i$ . Then,

\begin{align*} \left \|\xi _t^{i,N}-\xi _t^i \right \|^2\le 2L\int _0^t\Big [\left \|\xi _s^{i,N}-\xi _s^i \right \|^2+ \left \|\theta _s^N-\theta _s \right \|^2\Big ] \mathrm {d}s \qquad (i = 1,\ldots, N), \end{align*}

for $t \in [0,T]$ .

Proof. Recall that $(l^{1,N}_t,\ldots, l^{N,N}_t)_{t \geq 0}$ is non-decreasing in time and, hence, has finite total variation. We apply Itô’s formula to $\left \|\xi _t^{i,N}-\xi _t^i \right \|^2$ and obtain

\begin{align*} \left \|\xi _t^{i,N}-\xi _t^i \right \|^2= 2 \underbrace {\int _0^t \left \langle \xi _s^{i,N}-\xi _s^i,\nabla _x \Phi (\xi ^{i,N}_s,\theta ^N_s)-\nabla _x \Phi (\xi ^i_s,\theta _s)\right \rangle \mathrm {d}s}_{(I1)}\\ + \underbrace {2\int _0^t\left \langle n(\xi ^{i,N}_s), \xi _s^{i,N}-\xi _s^i \right \rangle \mathrm {d}l^{i,N}_s -2\int _0^t\left \langle n(\xi ^i_s), \xi _s^{i,N}-\xi _s^i \right \rangle \mathrm {d}l^i_s}_{(I2)}. \end{align*}

We first argue that $(I2)\le 0.$ Recall that $ n(x)=-x/\left \|x \right \|$ and that the processes $(\xi ^{i,N}_t)_{t \geq 0}$ and $(\xi ^{i}_t)_{t \geq 0}$ take values in the $\varepsilon$ -ball $B$ with $\varepsilon \lt 1$ . Then, we have

\begin{align*} 2\int _0^t\left \langle n(\xi ^{i,N}_s), \xi _s^{i,N}-\xi _s^i \right \rangle \mathrm {d}l^{i,N}_s&= 2\int _0^t\left \langle n(\xi ^{i,N}_s), \xi _s^{i,N}\right \rangle \mathrm {d}l^{i,N}_s- 2\int _0^t\left \langle n(\xi ^{i,N}_s), \xi _s^i \right \rangle \mathrm {d}l^{i,N}_s\\ &= -2 {\varepsilon } l^{i,N}_t- 2 \int _0^t\left \langle n(\xi ^{i,N}_s), \xi _s^i \right \rangle \mathrm {d}l^{i,N}_s\le -2{\varepsilon } l^{i,N}_t+2{\varepsilon }\int _0^t\mathrm {d}l^{i,N}_s= 0, \end{align*}

where the last inequality holds since $- 2 \int _0^t\left \langle n(\xi ^{i,N}_s), \xi _s^i \right \rangle \mathrm {d}l^{i,N}_s\leq 2 \int _0^t\left |\left \langle n(\xi ^{i,N}_s), \xi _s^i \right \rangle \right |\mathrm {d}l^{i,N}_s\leq 2{\varepsilon }\int _0^t\mathrm {d}l^{i,N}_s$ . Similarly, we have

\begin{align*} -2\int _0^t\left \langle n(\xi ^i_s), \xi _s^{i,N}-\xi _s^i \right \rangle \mathrm {d}l^i_s = 2\int _0^t\left \langle n(\xi ^i_s), \xi _s^i- \xi _s^{i,N }\right \rangle \mathrm {d}l^i_s \le 0. \end{align*}

Hence, we have $(I2)\le 0.$

For $(I1)$ , due to Assumption 3.1 and, again, due to the boundedness of $B,$ we have

\begin{align*} (I1)&\le L\int _0^t\left \|\xi _s^{i,N}-\xi _s^i \right \|\Big [\left \|\xi _s^{i,N}-\xi _s^i \right \|+ \left \|\theta _s^N-\theta _s \right \|\Big ] \mathrm {d}s \le 2L\int _0^t\Big [\left \|\xi _s^{i,N}-\xi _s^i \right \|^2+ \left \|\theta _s^N-\theta _s \right \|^2\Big ] \mathrm {d}s. \end{align*}

Finally, we study the distance between $\theta _t^N$ and $\theta _t$ for $t \geq 0$ .

Lemma 4.4. Let Assumption 3.1 hold. Then, we have

\begin{align*} \left \|\theta _t^N-\theta _t \right \|^2\le 3L \int _0^t\left \|\theta _s^N-\theta _s \right \|^2 \mathrm {d}s+\frac {2L}{N}\sum ^N_{i=1}\int _0^t \left \|\xi ^{i,N}_s-\xi _s^i \right \|^2\mathrm {d}s+2L\int _0^t{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s)\mathrm {d}s, \end{align*}

for $t \in [0,T].$

Proof. Due to Assumption 3.1 and since ${{\mathcal W}}_1(\mu ^N_s,\mu _s)\le {{\mathcal W}}_2(\mu ^N_s,\mu _s)$ , we have

(4.2) \begin{align} \left \|\theta _t^N-\theta _t \right \|^2 =& -2\int _0^t \left \langle \theta _s^N-\theta _s,G(\theta _s^N,\mu ^N_s)-G(\theta _s,\mu _s)\right \rangle \mathrm {d}s\nonumber \\ &\le 2L\int _0^t \left \|\theta _s^N-\theta _s \right \|\Big (\left \|\theta _s^N-\theta _s \right \|+{{\mathcal W}}_2(\mu ^N_s,\mu _s)\Big )\mathrm {d}s\nonumber \\ &\le 2L \int _0^t\left \|\theta _s^N-\theta _s \right \|^2 \mathrm {d}s+2L\int _0^t \left \|\theta _s^N-\theta _s \right \|{{\mathcal W}}_2(\mu ^N_s,\mu _s)\mathrm {d}s\nonumber \\ &\le 3L \int _0^t\left \|\theta _s^N-\theta _s \right \|^2 \mathrm {d}s+L\int _0^t {{\mathcal W}}^2_2(\mu ^N_s,\mu _s)\mathrm {d}s. \end{align}

The triangle inequality implies that

(4.3) \begin{align} {{\mathcal W}}^2_2(\mu ^N_s,\mu _s)\le 2{{\mathcal W}}^2_2(\mu ^N_s,N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i})+2{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s)\nonumber \\ \le \frac {2}{N}\sum ^N_{i=1}\left \|\xi ^{i,N}_s-\xi _s^i \right \|^2+2{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s). \end{align}

Combining (4.2) and (4.3), we obtain

\begin{align*} \left \|\theta _t^N-\theta _t \right \|^2\le 3L \int _0^t\left \|\theta _s^N-\theta _s \right \|^2 \mathrm {d}s+\frac {2L}{N}\sum ^N_{i=1}\int _0^t \left \|\xi ^{i,N}_s-\xi _s^i \right \|^2\mathrm {d}s+2L\int _0^t{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s)\mathrm {d}s. \end{align*}

We now proceed to the proof of Theorem4.1.

Proof of Theorem 4.1 We commence by constructing an upper bound for

\begin{equation*}u_t^N\,:\!=\,N^{-1}\sum ^N_{i=1} \left \|\xi ^{i,N}_t-\xi _t^i \right \|^2+ \left \|\theta _t^N-\theta _t \right \|^2.\end{equation*}

From Lemma 4.3 and Lemma 4.4, we have

\begin{align*} u_t^N&\le 5L\int _0^t u_s^N\mathrm {d}s+ 2L\int _0^t{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s)\mathrm {d}s. \end{align*}

Grönwall’s inequality implies that

\begin{align*} u_t^N\le 2Le^{5Lt}\int _0^t{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s)\mathrm {d}s. \end{align*}

According to Proposition 4.2, we have

\begin{align*} {\mathbb E}[ u_t^N]\le 2Le^{5Lt}\int _0^t{\mathbb E}[{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s)]\mathrm {d}s\le 2C_d Le^{(1+5L)t}o_{d,T,N}, \end{align*}

whereas (4.3) implies

\begin{align*} \left \|\theta _t^N-\theta _t \right \|^2+ {{\mathcal W}}^2_2(\mu ^N_s,\mu _s) \le u_t^N+2{{\mathcal W}}^2_2(N^{-1}\sum ^N_{i=1}\delta _{\xi _s^i},\mu _s). \end{align*}

Therefore,

\begin{align*} \sup _{t\in [0,T]}{\mathbb E}\big [\left \|\theta _t^N-\theta _t \right \|^2+{{\mathcal W}}^2_2(\mu _t^N,\mu _t)\big ]\le \sup _{t\in [0,T]}{\mathbb E}[u_t^N]+ \sup _{t\in [0,T]}{\mathbb E}\big [{{\mathcal W}}^2_2(\mu _t^N,\mu _t)\big ]\le C_{d,T}o_{d,T,N}, \end{align*}

where $C_{d,T}= 2C_d(1+ Le^{(1+5L)t}).$

5 Longtime behaviour of the McKean–Vlasov process

Theorem4.1 implies that the gradient flow approximation in Abram $(\theta _t^N)_{t \geq 0}$ converges to the corresponding part of the McKean–Vlasov SDE $(\theta _t)_{t \geq 0}$ given in (3.2). In this section, we show that this McKean–Vlasov SDE is able to find the minimiser $\theta _*$ of $F = \int _{B({\varepsilon })} \Phi (\xi, \cdot ) \pi ^{\gamma, \varepsilon }(\mathrm {d}\xi |\cdot ).$ This, thus, gives us a justification to use Abram to solve the Bayesian adversarial robustness problem. We start by showing that $F$ admits a minimiser.

Proof. We first argue that $F$ is bounded below and obtains a minumum at some point $\theta _*.$ From Subsection 3.2, we already know that $\Phi (0,\theta )$ is $2\lambda$ -strongly convex in $\theta$ . Without loss of generality, we assume $\Phi (0,0)=0$ and $\nabla _\theta \Phi (0,0)=0$ , that is $\Phi (0,\theta )$ reaches its minimum $0$ at $\theta _*=0.$ Since $\Phi (\xi, \cdot )$ is $2\lambda$ strongly convex for any $\xi \in B$ , we have that

(5.1) \begin{align} \Phi (\xi, \theta )\ge \Phi (\xi, 0)+ \theta \cdot \nabla _\theta \Phi (\xi, 0)+\lambda \left \|\theta \right \|^2. \end{align}

Assumption 3.1 implies that,

\begin{equation*}\left \|\nabla _\theta \Phi (\xi, 0) \right \|=\left \|\nabla _\theta \Phi (\xi, 0)-\nabla _\theta \Phi (0,0) \right \|\le L\left \|\xi \right \|\le L,\end{equation*}

and

\begin{equation*}\left |\Phi (\xi, 0)\right |= \left |\Phi (\xi, 0)-\Phi (0,0)\right |\le \sup _{\zeta \in B}\left \|\nabla _\xi \Phi (\zeta, 0) \right \|\left \|\xi \right \|\le (L+C_0)\left \|\xi \right \|\le L+C_0,\end{equation*}

where $C_0=\left \|\nabla _\xi \Phi (0,0) \right \|.$ Therefore, we have $\Phi (\xi, \theta )\ge -L-C_0- L\left \|\theta \right \|+\lambda \left \|\theta \right \|^2,$ which is bounded below by $-L-C_0-\frac {L^2}{4\lambda }.$ Thus, $F$ is bounded below by the same value. We can always choose some $R_0=R_0(L,\lambda, C_0)$ , such that for $\left \|\theta \right \|\ge R_0,$ $ \Phi (\xi, \theta )\ge C_0+L$ . Moreover, we already have $ \Phi (\xi, 0)\le L+C_0.$ Thus, $F(\theta ) \ge C_0+L$ when $\left \|\theta \right \|\ge R_0$ and $F(0) \le C_0+L$ . Hence, $F$ attains its minimum on the $R_0$ -ball $\{\theta \in X: \left \|\theta \right \|\le R_0\}.$

Before stating the main theorem of this section – the convergence of the McKean–Vlasov SDE to the minimiser of $F$ – we need to introduce additional assumptions.

Assumption 5.2 (Neumann Boundary Condition). Let $\Phi (\cdot, \theta )$ satisfy a Neumann boundary condition on $\partial B,$

\begin{align*} \frac {\partial _\xi \Phi (\xi, \theta )}{\partial n}= \nabla _\xi \Phi (\xi, \theta )\cdot n(\xi )=0, \end{align*}

for any $\theta \in X.$

For a general function $\Phi$ defined on $B$ , this assumption can be satisfied by smoothly extending $\Phi$ on $B'$ with radius $2{\varepsilon }$ such that it vanishes near the boundary of $B'$ . We shall see that this assumption guarantees the existence of the invariant measure of the auxiliary dynamical system (5.3) that we introduce below.

Assumption 5.3 (Small-Lipschitz). For any probability measures $\nu$ , $\tilde \nu$ on $(B, \mathcal {B}B)$ and $\theta \in {\mathbb {R}}^n,$

\begin{align*} \left \|G(\theta, \nu )-G(\theta, \tilde \nu ) \right \|\le \ell \left \|\nu -\tilde \nu \right \|_{{\textrm { TV}}}, \end{align*}

where $\ell = (\frac {(\delta \land \lambda )\sqrt {\lambda }e^{-t_0} }{4\sqrt {2}CL})\land (\frac {\sqrt {\lambda }}{\sqrt {2}L})$ and $t_0= t_0(\delta, \lambda, C)=(\delta \land \lambda )^{-1}\log (4C)$ . The constants $\delta$ and $C$ appear in Proposition 5.6 .

Equivalently, we may say that this assumption requires $G$ to have a small enough Lipschitz constant. If $\varepsilon$ (the radius of $B$ ) is very small, this assumption is implied by Assumption 3.1, since ${{\mathcal W}}_1(\nu, \tilde \nu )\le {\varepsilon }^d \int _B \int _B \boldsymbol {1}_{x\ne y}\pi (\mathrm d x,\mathrm d y)= {\varepsilon }^d \left \|\nu -\tilde \nu \right \|_{{\textrm { TV}}}.$

We illustrate these assumptions again in the linear-quadratic problem that we considered in Example 3.3 and show that Assumptions 5.2 and 5.3 can be satisfied in this case.

Example 5.4 (Example 3.3 continued). We consider again $\Phi (\xi, \theta ) = \left \|\xi -\theta \right \|^2$ with $\theta$ in a bounded $X' \subseteq X$ . Unfortunately, $\Phi$ does not satisfy Assumption 5.2 , since the term $(\xi -\theta )\cdot \xi$ is not necessary to be zero on the boundary of $B$ . Instead, we study a slightly larger ball by considering $\widehat {\varepsilon } = 2\varepsilon$ instead of $\varepsilon$ and also replace $\Phi$ by $\widehat {\Phi }(\xi, \theta )=\left \|m(\xi )-\theta \right \|^2,$ where $m:{\mathbb {R}}^d\to {\mathbb {R}}^d$ is smooth and equal to $\xi$ on the $\varepsilon$ -ball and vanishes near the boundary of the $2{\varepsilon }$ -ball. Since $m(\xi )$ varnishes near the boundary of $2\varepsilon$ -ball, $\widehat {\Phi }$ satisfies Assumption 5.2 .

We note that $\nabla _\xi \widehat {\Phi }(\xi, \theta )=2D_\xi m(\xi ) (m(\xi )-\theta ).$ Hence, $\nabla _\xi \widehat {\Phi }$ is Lipschitz in both $\theta$ and $\xi$ which directly follows from the boundedness and Lipschitz continuity of $m$ , $D_\xi m$ . Analogously to Example 3.3 , we have

\begin{align*} G(\theta, \nu )= 2\theta -2{\mathbb E}_\nu [m(\xi )]+4\theta \cdot \mathrm {Var}_\nu (m(\xi ))-2 \mathrm {Cov}_\nu (\left \|m(\xi ) \right \|^2,m(\xi )), \end{align*}

and also see that it still satisfies Assumptions 3.1 , 3.2 when $\theta$ is bounded and $\varepsilon$ is small. Finally, Assumption 5.3 is satisfied if $\varepsilon$ is chosen to be sufficiently small.

We are now able to state the main convergence theorem of this section. Therein, we still consider $\theta _*$ to be a minimiser of function of $F$ .

Theorem 5.5. Let Assumptions 3.1 , 3.2 , 5.2 , and 5.3 hold and let $(\theta _t, \mu _t)_{t \geq 0}$ be the solution to the McKean–Vlasov SDE (3.2) . Then, there are constants $\eta \gt 0$ and $\tilde C \gt 0$ with which we have

(5.2) \begin{align} \left \|\theta _t-\theta _* \right \|^2+ \left \| \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\le \tilde C \Big (\left \|\theta _0-\theta _* \right \|^2+ \left \| \mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big ) e^{-\eta t}. \end{align}

We can see this result as both a statement about the convergence of $(\theta _t^N)_{t \geq 0}$ to the minimiser, but also as an ergodicity statement about $(\theta _t^N,\xi _t)_{t \geq 0}$ . The ergodicity of a McKean–Vlasov SDE with reflection has also been subject of Theorem 3.1 in [Reference Wang53]. In their work, the process is required to have a non-degenerate diffusion term. Hence, their result does not apply immediately, since the marginal $(\theta _t)_{t \geq 0}$ is deterministic (conditionally on $(\xi _t)_{t \geq 0}$ ). Our proof ideas, however, are still influenced by [Reference Wang53].

We note additionally that Theorem5.5 implies the uniqueness of the minimiser $\theta _*$ – we had only shown existence in Proposition 5.1: If there exists another minimiser $\theta _*'$ , then the dynamics (3.2) is invariant at $(\theta _0,\xi _0)\sim \delta _{\theta _*'}\otimes \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*'})$ , which means $(\theta _t,\xi _t)\sim \delta _{\theta _*'} \otimes \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*'})$ for all $t\ge 0.$ Hence, we have $\left \|\theta '_*-\theta _* \right \|\le \tilde C\left \|\theta '_*-\theta _* \right \|e^{-\eta t}$ . The right-hand side vanishes as $t\to \infty, $ which implies $\theta _*'=\theta _*.$

In order to prove Theorem5.5, we first consider the case where $\theta _t\equiv \theta _*$ , i.e.

(5.3) \begin{align} \widehat \xi _t &=\xi _0+ \int _0^t\nabla _x \Phi (\widehat \xi _s,\theta _*)\mathrm {d}s + \sqrt {2}W_t+\int _0^t\nu (\widehat \xi _s)\mathrm {d}\widehat l_s. \end{align}

We denote the law of $\widehat \xi _t$ by $\widehat \mu _t$ , $t \geq 0$ . Motivated by [Reference Wang53], we first show the exponential ergodicity for the process $(\widehat \xi _t)_{t \geq 0}$ .

Proposition 5.6. Let Assumptions 3.1 and 5.2 hold. Then, $(\widehat \xi _t)_{t \geq 0}$ defined in (5.3) is well-posed and admits an unique invariant measure $\pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}).$ Moreover, $(\widehat \xi _t)_{t \geq 0}$ is exponentially ergodic. In particular, there exist $C,\delta \gt 0,$ such that

\begin{align*} \left \|\widehat \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\le C \left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}} e^{-\delta t}. \end{align*}

Proof. The well-posedness and exponential ergodicity is a direct corollary of ( [Reference Wang53], Theorem 2.3). We only need to verify that $\pi ^{\gamma, \varepsilon }(\cdot |{\theta _*})$ is invariant under the dynamics (5.3). We know that the probability distributions $(\widehat \mu _t)_{t \geq 0}$ satisfies the following linear PDE with Neumann boundary condition

\begin{align*} \partial _t \widehat \mu _t = \Delta \widehat \mu _t-\mathrm {div} (\widehat \mu _t\nabla _\xi \Phi (\xi, \theta _*)),\qquad \frac {\partial \widehat \mu _t}{\partial n}\Big |_{\partial B}=0. \end{align*}

So any invariant measure of the dynamics (5.3) is a probability distribution that solves the following stationary PDE

\begin{align*} \Delta \widehat \mu -\mathrm {div} (\widehat \mu \nabla _\xi \Phi (\xi, \theta _*))=0,\qquad \frac {\partial \widehat \mu }{\partial n}\Big |_{\partial B}=0. \end{align*}

Now, $\widehat \mu =\pi ^{\gamma, \varepsilon }(\cdot |{\theta _*})$ is a basic result in the theory of Langevin SDEs with reflection, see, e.g. [Reference Sato, Takeda, Kawai and Suzuki44].

Most of the time, we are not able to quantify the constants $C$ and $\delta$ : the Harris-like theorem from [Reference Wang53] is not quantitative. A special case in which we can quantify $C$ and $\delta$ is when the potential separates in the sense that $\nabla _\xi \Phi (\xi, \theta _*)= (f_1(\xi _1, \theta _*),\ldots, f_{d_Y}(\xi _{d_Y}, \theta _*))$ . Then (5.3) can be viewed as $d_Y$ independent reflection SDEs. If we denote their ergodicity constants as $C_i$ and $\delta _i$ for $i=1,\ldots, d_Y$ , then ( [Reference Jin, Latz, Liu and Schönlieb22], Proof of Proposition 1) implies that we can choose $C\,:\!=\,\sum _{i=1}^d C_i$ and $\delta \,:\!=\,\min _{i=1,\ldots, d}\delta _i$ . Thus, in this case, the constant $C$ is linear in the dimension $d.$

Next, we bound the distance $\left \|\mu _t- \widehat \mu _t \right \|_{{\textrm { TV}}}$ by Girsanov’s theorem – a classical way to estimate the distance between two SDEs with different drift terms. This is again motivated by ( [Reference Wang53], proof of Lemma 3.2). There, the method is used to bound the distance between two measure-dependent SDEs. In our case, it also involves the state $\theta _t$ , which depends on $t.$ Hence, the right-hand side depends on the path of $(\theta _s)_{0\le s\le t}.$

Lemma 5.7. Let Assumption 3.1 hold. Then, we have

\begin{align*} \left \|\mu _t- \widehat \mu _t \right \|^2_{{\textrm { TV}}}\le L^2 \int _0^t\left \|\theta _s-\theta _* \right \|^2 \mathrm {d}s. \end{align*}

Proof. We follow the same idea as ( [Reference Wang53], proof of Lemma 3.2). In our case, we need to choose

\begin{align*} Z_t= \exp \Big (\int _0^t z(\theta _*,\theta _s,\xi _s)\cdot \mathrm {d}W_s-\frac {1}{2}\int _0^t \left \|z(\theta _*,\theta _s,\xi _s) \right \|^2\mathrm {d}s \Big ), \end{align*}

where $z(\theta _*,\theta, x)= (\nabla _x \Phi (x,\theta )-\nabla _x \Phi (x,\theta _*))/\sqrt {2}$ . ( [Reference Gall29], Proposition5.6) implies that the process $(Z_t)_{t \geq 0}$ is a martingale due to $z(\theta _*,\theta _s,\xi _s)$ being bounded and $\int _0^t \left \|z(\theta _*,\theta _s,\xi _s) \right \|^2\mathrm {d}s$ being the quadratic variation process of $\int _0^t z(\theta _*,\theta _s,\xi _s)\cdot \mathrm {d}W_s$ .

We define the probability measure $\mathbb {Q}_t\,:\!=\, Z_t{\mathbb {P}},$ i.e. $\mathbb {Q}_t(A)\,:\!=\, {\mathbb E}[ Z_t \boldsymbol {1}_A]$ for any $\mathcal {F}_t$ -measurable set $A$ . And we notice that the quadratic covariation between $\int _0^t z(\theta _*,\theta _s,\xi _s)\cdot \mathrm {d}W_s$ and $W_t$ is given by

\begin{align*} \left \langle \int _0^. z(\theta _*,\theta _s,\xi _s)\cdot \mathrm {d}W_s,W_.\right \rangle _t= \int _0^t z(\theta _*,\theta _s,\xi _s)\mathrm {d}s. \end{align*}

Hence by Girsanov’s theorem (see ([Reference Gall29], Theorem 5.8, Conséquences (c))]), $\tilde W_t\,:\!=\, W_t-\int _0^t z(\theta _*,\theta _s,\xi _s)\mathrm {d}s$ is a Brownian motion under $\mathbb {Q}_t$ with the same filtration $\mathcal {F}_t$ .

We rewrite (3.2) as

\begin{align*} \xi _t &=\xi _0+ \int _0^t\nabla _x \Phi (\xi _s,\theta _*)\mathrm {d}s + \sqrt {2}\tilde W_t+\int _0^tn(\xi _s)\mathrm {d}l_s, \end{align*}

which has the same distribution as $\widehat \xi _t$ under $\mathbb {Q}_t.$ Hence

\begin{align*} \left \|\mu _t- \widehat \mu _t \right \|_{{\textrm { TV}}}=& \sup _{\left |f\right |\le 1}\left |{\mathbb E}[f(\xi _t)]- {\mathbb E}[f(\xi _t)Z_t]\right |\le {\mathbb E}[\left |Z_t-1\right |]\\ \le & 2{\mathbb E}[R_t\log (R_t)]^{\frac {1}{2}}=2 {\mathbb E}_{Q_t}\Big [\int _0^t z(\theta _*,\theta _s,\xi _s)\cdot \mathrm {d}W_s-\frac {1}{2}\int _0^t \left \|z(\theta _*,\theta _s,\xi _s) \right \|^2\mathrm {d}s\Big ]^{\frac {1}{2}}\\ =& 2 {\mathbb E}_{Q_t}\Big [\int _0^t z(\theta _*,\theta _s,\xi _s)\cdot \mathrm {d}\tilde W_s+\frac {1}{2}\int _0^t \left \|z(\theta _*,\theta _s,\xi _s) \right \|^2\mathrm {d}s\Big ]^{\frac {1}{2}}\\ =& \sqrt {2} {\mathbb E}_{Q_t}\Big [\int _0^t \left \|z(\theta _*,\theta _s,\xi _s) \right \|^2\mathrm {d}s\Big ]^{\frac {1}{2}}\le L\Big (\int _0^t\left \|\theta _s-\theta _* \right \|^2 \mathrm {d}s\Big )^{\frac {1}{2}}. \end{align*}

where the first “ $\leq$ ” is implied by Pinsker’s inequality.

Using these auxiliary results, we can now formulate the proof of Theorem5.5.

Proof of Theorem 5.5 We take the time derivative of $\left \|\theta _t-\theta _* \right \|^2,$

\begin{align*} \frac {\mathrm {d}\left \|\theta _t-\theta _* \right \|^2}{\mathrm {d}t}=& - \left \langle G(\theta _t,\mu _t)-G(\theta _*,\pi ^{\gamma, \varepsilon }(\cdot |{\theta _*})),\theta _t-\theta _*\right \rangle \\ &\le -2\lambda \left \|\theta _t-\theta _* \right \|^2+\ell \left \|\theta _t-\theta _* \right \|\left \|\mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|_{{\textrm { TV}}}\\ &\le -\lambda \left \|\theta _t-\theta _* \right \|^2+\frac {\ell ^2}{\lambda } \left \|\mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}, \end{align*}

where the first “ $\leq$ ” is due to the $\varepsilon$ -Young’s inequality. This implies

\begin{equation*}\frac {\mathrm {d}(e^{\lambda t}\left \|\theta _t-\theta _* \right \|^2)}{\mathrm {d}t}\le \frac {\ell ^2}{\lambda }e^{\lambda t} \left \|\mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}.\end{equation*}

Hence, we have

(5.4) \begin{align} \left \|\theta _t-\theta _* \right \|^2\le e^{-\lambda t}\left \|\theta _0-\theta _* \right \|^2+\frac {\ell ^2}{\lambda }\int _0^t \left \|\mu _s- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\mathrm {d}s. \end{align}

Then, using the triangle inequality, we see that

\begin{align*} \left \|\theta _t-\theta _* \right \|^2+ m\left \| \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}&\le \underbrace { \left \|\theta _t-\theta _* \right \|^2}_{(5.4)}+\underbrace {2m\left \| \mu _t- \widehat \mu _t \right \|^2_{{\textrm { TV}}}}_{Lemma 5.7}+\underbrace {2m\left \| \widehat \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}}_{Proposition 5.6} \\ &\le \int _0^t \Big (\frac {\ell ^2}{\lambda }\left \|\mu _s-\pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}+2mL^2\left \|\theta _s-\theta _* \right \|^2\Big )\mathrm {d}s\\ &\qquad +2C\Big (\left \|\theta _0-\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )e^{-(\delta \land \lambda ) t}. \end{align*}

Let $m=m(\ell, L,\lambda )=\frac {\ell }{L\sqrt {2\lambda }}$ , we conclude from the above inequality that

\begin{align*} \left \|\theta _t-\theta _* \right \|^2+ m\left \| \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}&\le 2mL^2\int _0^t \Big (m\left \|\mu _s-\pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}+\left \|\theta _s-\theta _* \right \|^2\Big )\mathrm {d}s\\ &\qquad +2C\Big (\left \|\theta _0-\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )e^{-(\delta \land \lambda ) t}. \end{align*}

Hence, by Grönwall’s inequality, we have

(5.5) \begin{align} \left \|\theta _t-\theta _* \right \|^2&+ m\left \| \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}} \nonumber \\ &\le C\Big (\left \|\theta _0-\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big ) \Big (2mL^2\int _0^t e^{2mL^2(t-s)} e^{-(\delta \land \lambda ) s}\mathrm {d}s+e^{-(\delta \land \lambda ) t}\Big )\nonumber \\ &= C\Big (\frac {2mL^2}{2mL^2+\delta \land \lambda }(e^{2mL^2 t}-e^{-(\delta \land \lambda )t})+e^{-(\delta \land \lambda ) t}\Big )\Big (\left \|\theta _0-\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )\nonumber \\ &\le C\Big (\frac {2mL^2}{\delta \land \lambda } e^{2mL^2 t}+e^{-(\delta \land \lambda ) t}\Big )\Big (\left \|\theta _0-\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )\nonumber \\ &\le C_{t, L,\ell, \lambda }\Big (\left \|\theta _0-\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big ), \end{align}

where $C_{t, L,\ell, \lambda }= C\Big (\frac {2mL^2}{\delta \land \lambda } e^{2mL^2 t}+e^{-(\delta \land \lambda ) t}\Big ).$ According to Assumption 5.3, we know that $2mL^2=\frac {\ell L\sqrt {2}}{\sqrt {\lambda }}\le 1$ . Next, we are going to show that $0\lt C_{t_0, L,\ell, \lambda }\le 1/2$ for $t_0=t_0(\delta, \lambda, C)=(\delta \land \lambda )^{-1}\log (4C).$ Again, from Assumption 5.3, we know $\frac {2mL^2}{\delta \land \lambda } e^ {t_0}\le \frac {1}{4C}$ . Hence we finally have,

\begin{align*} C_{t_0, L,\ell, \lambda }\le \frac {2CmL^2}{\delta \land \lambda } e^ {t_0}+ Ce^{-(\delta \land \lambda ) t_0}\le \frac {1}{2}. \end{align*}

For any $t\ge 0,$ we always have $[\frac {t}{t_0}]t_0\le t \lt [\frac {t}{t_0}]t_0+t_0,$ where $[x]$ denotes the greatest integer $\leq x.$ Hence,

\begin{align*} \left \|\theta _t-\theta _* \right \|^2+ m\left \| \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}&\le 2^{-[\frac {t}{t_0}]}\Big (\left \|\theta _{t- [\frac {t}{t_0}]t_0}-\theta _* \right \|^2+m\left \|\mu _{t- [\frac {t}{t_0}]t_0}- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )\\ &\le 2^{-\frac {t}{t_0}+1}\sup _{0\le s\le t_0}\Big (\left \|\theta _s -\theta _* \right \|^2+m\left \|\mu _s- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )\\ &\le 2^{-\frac {t}{t_0}+1}C\Big (\frac {e^{t_0}}{\delta \land \lambda } +1\Big )\Big (\left \|\theta _0 -\theta _* \right \|^2+m\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big ), \end{align*}

where the last inequality is from (5.5) and $C_{s, L,\ell, \lambda }$ could be bounded by $C(\frac {e^{t_0}}{\delta \land \lambda } +1)$ for $0\le s\le t_0$ . And since $m\le \frac {1}{2L^2}\lt 1,$ we conclude that

\begin{align*} \left \|\theta _t-\theta _* \right \|^2+ \left \| \mu _t- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}&\le m^{-1}2^{-\frac {t}{t_0}+1}C\Big (\frac {e^{t_0}}{\delta \land \lambda } +1\Big )\Big (\left \|\theta _0 -\theta _* \right \|^2+\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big )\\ &\le 2L^2 2^{-\frac {t}{t_0}+1}C\Big (\frac {e^{t_0}}{\delta \land \lambda } +1\Big )\Big (\left \|\theta _0 -\theta _* \right \|^2+\left \|\mu _0- \pi ^{\gamma, \varepsilon }(\cdot |{\theta _*}) \right \|^2_{{\textrm { TV}}}\Big ). \end{align*}

Finally, we choose the constants $\eta =\eta (\delta, \lambda, C)= \log (2)t_0^{-1}=(\delta \land \lambda )\frac {\log (2)}{\log (4C)}$ and $\tilde C= \tilde C(L,C,\delta, \lambda )= 4CL^2\Big (\frac {e^{t_0}}{\delta \land \lambda } +1\Big )= 4CL^2\Big (\frac {(4C)^{(\delta \land \lambda )^{-1}}}{\delta \land \lambda } +1\Big ) .$

6 Algorithmic considerations

Throughout this work, we have considered Abram as a continuous-time dynamical system. To employ it for practical adversarially robust machine learning, this system needs to be discretised, i.e. we need to employ a time stepping scheme to obtain a sequence $(\theta ^N_k, \xi _k^{1, N}, \ldots, \xi _k^{N,N})_{k=1}^\infty$ that approximates Abram at discrete points in time. We now propose two discrete schemes for Abram, before then discussing the simulation of Bayesian adversarial attacks.

6.1 Discrete Abram

We initialise the particles by sampling them from the uniform distribution in the $\varepsilon$ -ball. Then, we employ a projected Euler–Maruyama scheme to discretise the particles $(\xi _t^{1, N}, \ldots, \xi _t^{N,N})_{t \geq 0}$ . The Euler–Maruyama scheme (see, e.g. [Reference Higham and Kloeden19]) is a standard technique for first order diffusion equation—we use a projected version to adhere to the reflecting boundary condition inside the ball $B$ . Projected Euler–Maruyama schemes of this form have been studied in terms of almost sure convergence [Reference Słomiński49] and, importantly, also in terms of their longtime behaviour [Reference Lamperski, Belkin and Kpotufe27]. The gradient flow part $(\theta ^N_t)_{t \geq 0}$ is discretised using a forward Euler method – turning the gradient flow into a gradient descent algorithm [Reference Nocedal and Wright39]. In applications, it is sometimes useful to allow multiple iterations of the particle dynamics $(\xi _t^{1, N}, \ldots, \xi _t^{N,N})_{t \geq 0}$ per iteration of the gradient flow $(\theta ^N_t)_{t \geq 0}$ . This corresponds to a linear time rescaling in the particle dynamics that should lead to a more accurate representation of the respective adversarial distribution.

If the number of data points $(y_k, z_k)_{k=1}^K$ is large, we may be required to use a data subsampling technique. Indeed, we approximate $\frac {1}{K}\sum _{k=1}^K \Phi (y_k, z_k|\theta ) \approx \Phi (y_{k'}, z_{k'})$ with a $k' \sim \mathrm {Unif}(\{1,\ldots, K\})$ being sampled independently in every iteration of the algorithm. This gives us a stochastic gradient descent-type approximation of the gradients in the algorithm, see [Reference Robbins and Monro42]. We note that we have not analysed data subsampling within Abram – we expect that techniques from [Reference Jin, Latz, Liu and Schönlieb22, Reference Latz28] may be useful to do so. We summarise the method in Algorithm1.

Algorithm 1 Abram

Algorithm 2 Mini-batching Abram

6.3 Bayesian attacks

The mechanism used to approximate the Bayesian adversary in Algorithm1 can naturally be used as a Bayesian attack. We propose two different attacks:

1. 1. We use the projected Euler–Maruyama method to sample from the Bayesian adversarial distribution $\pi ^{\gamma, \varepsilon }$ corresponding to an input dataset $y \in Y$ and model parameter $\theta ^*$ . We summarise this attack in Algorithm3.

2. 2. Instead of attacking with a sample from $\pi ^{\gamma, \varepsilon }$ , we can attack with the mean of said distribution. From Proposition 5.6, we know that the particle system $(\widehat {\xi }_t)_{t \geq 0}$ that is based on a fixed parameter $\theta _*$ , is exponentially ergodic. Thus, we approximate the mean of $\pi ^{\gamma, \varepsilon }$ , by sampling $(\widehat {\xi }_t)_{t \geq 0}$ using projected Euler–Maruyama and approximate the mean by computing the sample mean throughout the sampling path. We summarise this method in Algorithm4.

Algorithm 3 Bayesian sample attack

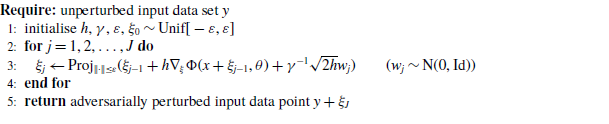
Algorithm 4 Bayesian mean attack

7 Deep learning experiments

We now study the application of Abram in deep learning. The model parameter $\theta$ is updated with batch size/number of particles $N$ . For each particle in the ensemble, the perturbation parameter $\xi$ is updated for $T$ steps. Each experimental run is conducted on a single Nvidia A6000 GPU.

7.1 MNIST

We test Algorithm1 and Algorithm2 on the classification benchmark data set MNIST [Reference LeCun and Cortes30] against different adversarial attacks and compare the results with the results after an FGSM-based [Reference Wong, Rice and Kolter57] adversarial training. We utilise the Adversarial Robustness Toolbox (ART) for the experiments, see [Reference Nicolae, Sinn, Tran, Buesser, Rawat, Wistuba, Zantedeschi, Baracaldo, Chen, Ludwig, Molloy and Edwards37] for more details. ART is a Python library for adversarial robustness that provides various APIs for defence and attack. We use a neural network with two convolution layers each followed by a max pooling. In Algorithm1, we set $\gamma =1, h=\varepsilon, \varepsilon =0.2$ . In Algorithm2, we set $\gamma =1, h=10\varepsilon, \varepsilon =0.2$ . We observe that setting larger noise scale for the attack during training helps Abram’s final evaluation performance. We train the neural network for 30 epochs (i.e. 30 full iterations through the data set) for each method. The number of particles (and batch size) is $N=128$ , and the inner loop is trained for $T=10$ times. To better understand how Abram responds to different attacks, we test against six attack methods: PGD [Reference Madry, Makelov, Schmidt, Tsipras and Vladu32], Auto-PGD [Reference Croce and Hein9], Carlini and Wagner [Reference Carlini and Wagner6], Wasserstein Attack [Reference Wong, Schmidt and Kolter56], as well as the Bayesian attacks introduced in this paper – see Algorithms3 and 4. We also test the method’s accuracy in the case of benign (non-attacked) input data. For the Bayesian sample attack and Bayesian mean attack, we set $\gamma =1000$ . See Table 2 for the comparison. The results are averaged over three random seeds. We observe that Abram performs similarly to FGSM under Wasserstein, Bayesian sample and Bayesian mean attack. FGSM outperforms Abram under Auto-PGD, PGD and Carlini & Wagner attack. We conclude that Abram is as effective as FGSM under certain weaker attacks, but can usually not outperform the conventional FGSM.

Table 2. Comparison of test accuracy (%) on MNIST with different adversarial attack after Abram, mini-batching Abram, and FGSM [Reference Wong, Rice and Kolter57] adversarial training

Another observation is that mini-batching Abram outperforms Abram significantly. Recall that in Abram we have used $128$ particles for each data point which can be viewed as SGD with batch size $1$ , whereas the mini-batching Abram is similar to the mini-batching SGD. Mini-batching Abram has the freedom to set the batch size which helps to reduce the variance in the stochastic optimisation and, thus, gives more stable results. In particular, with mini-batching Abram, gradients are approximated by multiple data points instead of one data point which is the case in Abram. Having a larger batch size also increases computation efficiency by doing matrix multiplication on GPUs, which is important in modern machine learning applications as the datasets can be expected to be large.

7.2 CIFAR10

Similarly, we test Algorithm2 on the classification benchmark dataset CIFAR10 [Reference Krizhevsky23] by utilising ART. The dataset is pre-processed by random crop and random horizontal flip following [Reference Krizhevsky23] for data augmentation. The neural network uses the Pre-act ResNet-18 [Reference He, Zhang, Ren and Sun18] architecture. For Abram, we set $\gamma =1, h=\varepsilon, \varepsilon =16/255$ . Similar as in the MNIST experiments, practically we find that setting larger noise scale for attack in training Abram helps to obtain a better final evaluation performance. The batch size $N=128$ and the inner loop is simulated for $T=10$ times. We train both mini-batching Abram and FGSM for 30 epochs. Due to its worse performance for MNIST and the large size of CIFAR10, we have not used the non-mini-batching version of Abram in this second problem. For the Bayesian sample attack and the Bayesian mean attack, we set $\gamma =1000$ . We present the results in Table 3. There, we observe that mini-batching Abram outperforms FGSM under Wasserstein and the Bayesian attacks, but not in any of the other cases.

Table 3. Comparison of test accuracy (%) on CIFAR10 with different adversarial attack after mini-batching Abram and FGSM [Reference Wong, Rice and Kolter57] adversarial training