Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T07:48:07.699Z Has data issue: false hasContentIssue false
  • English
  • Français

Entire solutions of the Fisher–KPP equation on the half line

Part of: Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  26 March 2019

BENDONG LOU ,
JUNFAN LU  and
YOSHIHISA MORITA
BENDONG LOU
Affiliation:
Department of Mathematics, Mathematics & Science College, Shanghai Normal University, Shanghai200234, China email: [email protected]
JUNFAN LU
Affiliation:
School of Mathematical Sciences, Tongji University, Shanghai200092, China email: [email protected]
YOSHIHISA MORITA
Affiliation:
Department of Applied Mathematics and Informatics, Ryukoku University, Seta Otsu520-2194, Japan email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the entire solutions of the Fisher–KPP (Kolmogorov–Petrovsky–Piskunov) equation ut = uxx + f(u) on the half line [0, ∞) with Dirichlet boundary condition at x = 0. (1) For any 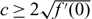$c \ge 2\sqrt {f'(0)} $, we show the existence of an entire solution 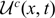${{\cal U}^c}(x,t)$ which connects the traveling wave solution φc(x + ct) at t = −∞ and the unique positive stationary solution V(x) at t = +∞; (2) We also construct an entire solution 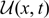${{\cal U}}(x,t)$ which connects the solution of ηt = f(η) at t = −∞ and V(x) at t = +∞.

Keywords

Reaction–diffusion equationFisher–KPP equationentire solutiontraveling wave solution

MSC classification

Primary: 35K57: Reaction-diffusion equations
Secondary: 35B08: Entire solutions 35B40: Asymptotic behavior of solutions
Type
Papers
Information
European Journal of Applied Mathematics , Volume 31 , Issue 3 , June 2020 , pp. 407 - 422
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This research was partly supported by the NSFC (No. 11671262) and JSPS KAKENHI Grant Number, 18H01139, 26247013 and JST CREST Grant Number JPMJCR14D3.

References

Aronson, D. G. & Weinberger, H. F. (1975) Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. In: Partial Differential Equations and Related Topics, Lecture Notes in Mathematics. Vol. 446, Springer, Berlin, pp. 5–49.CrossRefGoogle Scholar
Chen, X. & Guo, J.-S. (2005) Existence and uniqueness of entire solutions for a reaction–diffusion equation. J. Differ Equ. 212, 62–84.CrossRefGoogle Scholar
Chen, X., Guo, J.-S. & Ninomiya, H. (2006) Entire solutions of reaction–diffusion equations with balanced bistable nonlinearities. Proc. R. Soc. Edinb. Sect. A. 136, 1207–1237.CrossRefGoogle Scholar
Du, Y. & Lou, B. (2015) Spreading and vanishing in nonlinear diffusion problems with free boundaries. J. Eur. Math. Soc. 17, 2673–2724.CrossRefGoogle Scholar
Du, Y. & Matano, H. (2010) Convergence and sharp thresholds for propagation in nonlinear diffusion problems. J. Eur. Math. Soc. 12, 279–312.CrossRefGoogle Scholar
Fife, P. C. & Mcleod, J. B. (1977) The approach of solutions of nonlinear diffusion equations to travelling front solutions. Arch. Ration. Mech. Anal. 65, 335–361.CrossRefGoogle Scholar
Fukao, Y.Morita, Y. & Ninomiya, H. (2004) Some entire solutions of the Allen–Cahn equation. Taiwan. J. Math. 8, 15–32.CrossRefGoogle Scholar
Gu, H., Lou, B. & Zhou, M. (2015) Long time behavior of solutions of Fisher–KPP equation with advection and free boundaries. J. Funct. Anal. 269, 1714–1768.CrossRefGoogle Scholar
Guo, J.-S. & Morita, Y. (2005) Entire solutions of reaction–diffusion equations and an application to discrete diffusive equations. Discrete Contin. Dynam. Syst. 12, 193–212.CrossRefGoogle Scholar
Hamel, F. & Nadirashvili, N. (1999) Entire solutions of the KPP equation. Comm. Pure Appl. Math. 52, 1255–1276.3.0.CO;2-W>CrossRefGoogle Scholar
Kolmogorov, A. N., Petrovski, I. G. & Piskunov, N. S. (1937) A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem. Bull. Moscow Univ. Math. Mech. 1, 1–25.Google Scholar
Li, W., Sun, Y. & Wang, Z. (2010) Entire solutions in the Fisher–KPP equation with nonlocal dispersal. Nonlinear Anal. RWA. 11, 2302–2313.CrossRefGoogle Scholar
Morita, Y. & Ninomiya, H. (2006) Entire solutions with merging fronts to reaction–diffusion equations. J. Dynam. Differ. Equ. 18, 841–861.CrossRefGoogle Scholar
Morita, Y. & Ninomiya, H. (2010) Traveling wave solutions and entire solutions to reaction–diffusion equations. Sugaku Expositions, 23, 213–233 (Selected translation of Sugaku, Am. Math. Soc.).Google Scholar
Sun, Y., Li, W. & Wang, Z. (2011) Entire solutions in nonlocal dispersal equations with bistable nonlinearity. J. Differ. Equ. 251, 551–581.CrossRefGoogle Scholar
Wang, Z., Li, W. & Ruan, S. (2009) Entire solutions in bistable reaction–diffusion equations with nonlocal delayed nonlinearity. Trans. Am. Math. Soc. 361, 2047–2084.CrossRefGoogle Scholar
Wang, Z., Li, W. & Ruan, S. (2013) Entire solutions in lattice delayed differential equations with nonlocal interaction: bistable cases. Math. Model. Nat. Phenom. 8, 78–103.CrossRefGoogle Scholar
Wu, S., Shi, Z. & Yang, F. (2013) Entire solutions in periodic lattice dynamical systems. J. Differ. Equ. 255, 3505–3535.CrossRefGoogle Scholar
Yagisita, H. (2003) Backward global solutions characterizing annihilation dynamics of travelling fronts. Publ. Res. Inst. Math. Sci. 39, 117–164.CrossRefGoogle Scholar