Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Matioc, Anca-Voichita
and
Matioc, Bogdan-Vasile
2021.
The Muskat problem with surface tension and equal viscosities in subcritical $$L_p$$-Sobolev spaces.
Journal of Elliptic and Parabolic Equations,
Vol. 7,
Issue. 2,
p.
635.
Matioc, Bogdan–Vasile
and
Prokert, Georg
2021.
Two-phase Stokes flow by capillarity in full 2D space: an approach via hydrodynamic potentials.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 151,
Issue. 6,
p.
1815.
Matioc, Bogdan–Vasile
and
Prokert, Georg
2022.
Two-phase Stokes flow by capillarity in the plane: The case of different viscosities.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 29,
Issue. 5,
Chen, Ke
Nguyen, Quoc-Hung
and
Xu, Yiran
2022.
The Muskat problem with 𝐶¹ data.
Transactions of the American Mathematical Society,
Matioc, Bogdan-Vasile
and
Prokert, Georg
2023.
Capillarity-driven Stokes flow: the one-phase problem as small viscosity limit.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 74,
Issue. 6,
Shi, Jia
2023.
Regularity of Solutions to the Muskat Equation.
Archive for Rational Mechanics and Analysis,
Vol. 247,
Issue. 3,
Matioc, Anca–Voichita
and
Matioc, Bogdan–Vasile
2023.
A new reformulation of the Muskat problem with surface tension.
Journal of Differential Equations,
Vol. 350,
Issue. ,
p.
308.
García-Juárez, Eduardo
Gómez-Serrano, Javier
Haziot, Susanna V.
and
Pausader, Benoît
2024.
Desingularization of Small Moving Corners for the Muskat Equation.
Annals of PDE,
Vol. 10,
Issue. 2,
Paduro, Esteban
2024.
The second iterate of the Muskat equation in supercritical spaces.
Nonlinearity,
Vol. 37,
Issue. 4,
p.
045008.
Escher, Joachim
Matioc, Anca‐Voichita
and
Matioc, Bogdan‐Vasile
2024.
The Mullins–Sekerka problem via the method of potentials.
Mathematische Nachrichten,
Vol. 297,
Issue. 5,
p.
1960.
Shi, Jia
2024.
The regularity of the solutions to the Muskat equation: The degenerate regularity near the turnover points.
Advances in Mathematics,
Vol. 454,
Issue. ,
p.
109850.
Sánchez, Omar
2025.
Unbounded solutions for the Muskat problem.
Nonlinearity,
Vol. 38,
Issue. 2,
p.
025014.
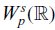 $W_p^s(\mathbb R)$
with s = 1+1/p is a critical space for this problem. We prove, for each s ∈ (1+1/p, 2) that the Rayleigh–Taylor condition identifies an open subset of
$W_p^s(\mathbb R)$
with s = 1+1/p is a critical space for this problem. We prove, for each s ∈ (1+1/p, 2) that the Rayleigh–Taylor condition identifies an open subset of 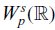 $W_p^s(\mathbb R)$
within which the Muskat problem is of parabolic type. This enables us to establish the local well-posedness of the problem in all these subcritical spaces together with a parabolic smoothing property.
$W_p^s(\mathbb R)$
within which the Muskat problem is of parabolic type. This enables us to establish the local well-posedness of the problem in all these subcritical spaces together with a parabolic smoothing property.