Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T07:12:16.146Z Has data issue: false hasContentIssue false
  • English
  • Français

A contact problem for viscoelastic bodies with inertial effects and unilateral boundary constraints

Published online by Cambridge University Press:  07 March 2016

RICCARDO SCALA  and
GIULIO SCHIMPERNA
RICCARDO SCALA
Affiliation:
Dipartimento di Matematica, Università di Pavia, Via Ferrata 1, 27100 Pavia, Italy email: [email protected], [email protected] Weierstrass Institute for Applied Analysis and Stochastics, Mohrenstr. 39, 10117 Berlin, Germany email: [email protected]
GIULIO SCHIMPERNA
Affiliation:
Dipartimento di Matematica, Università di Pavia, Via Ferrata 1, 27100 Pavia, Italy email: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a viscoelastic body occupying a smooth bounded domain 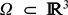$\Omega\subset \mathbb{R}^3$ under the effect of a volumic traction force g . The macroscopic displacement vector from the equilibrium configuration is denoted by u. Inertial effects are considered; hence, the equation for u contains the second-order term u tt . On a part ΓD of the boundary of Ω, the body is fixed and no displacement may occur; on a second part Γ N ⊂ ∂Ω, the body can move freely; on a third portion Γ C ⊂ ∂Ω, the body is in adhesive contact with a solid support. The boundary forces acting on ΓC due to the action of elastic stresses are responsible for delamination, i.e., progressive failure of adhesive bonds. This phenomenon is mathematically represented by a non-linear ordinary differential equation settled on ΓC and describing the evolution of the delamination order parameter z. Following the lines of a new approach outlined in Bonetti et al. (2015, arXiv:1503.01911) and based on duality methods in Sobolev–Bochner spaces, we define a suitable concept of weak solution to the resulting system of partial differential equations. Correspondingly, we prove an existence result on finite-time intervals of arbitrary length.

Keywords

second order parabolic equationviscoelasticityweak formulationcontact problemadhesionmixed boundary conditionsduality
Type
Papers
Information
European Journal of Applied Mathematics , Volume 28 , Issue 1 , February 2017 , pp. 91 - 122
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Attouch, H. (1984) Variational Convergence for Functions and Operators, Pitman, London.Google Scholar
[2] Barboteu, M., Bartosz, K. & Kalita, P. (2015) A dynamic viscoelastic contact problem with normal compliance, finite penetration and nonmonotone slip rate dependent friction. Nonlinear Anal. Real World Appl. 22, 452–472.Google Scholar
[3] Barbu, V., Colli, P., Gilardi, G. & Grasselli, M. (2000) Existence, uniqueness, and longtime behavior for a nonlinear Volterra integrodifferential equation. Differ. Integral Equ. 13, 1233–1262.Google Scholar
[4] Barbu, V. (1976) Nonlinear Semigroups and Differential Equations in Banach Spaces, Noord-hoff, Leyden.Google Scholar
[5] Blanchard, D., Damlamian, A. & Ghidouche, H. (1989) A nonlinear system for phase change with dissipation. Differ. Integral Equ. 2, 344–362.Google Scholar
[6] Bonetti, E., Bonfanti, G. & Rossi, R. (2008) Global existence for a contact problem with adhesion. Math. Methods Appl. Sci. 31, 1029–1064.Google Scholar
[7] Bonetti, E., BonfantiG. & Rossi, R. (2012) Analysis of a unilateral contact problem taking into account adhesion and friction. J. Differ. Equ. 235, 438–462.Google Scholar
[8] Bonetti, E., Rocca, E., Scala, R. & Schimperna, G. (2015) On the strongly damped wave equation with constraint, arXiv:1503.01911, submitted.Google Scholar
[9] Brézis, H. (1973) Opérateurs Maximaux Monotones et Semi-groupes de Contractions dans les Espaces de Hilbert, North-Holland Math. Studies, Vol. 5, North-Holland, Amsterdam.Google Scholar
[10] Brézis, H. (1972) Intégrales convexes dans les espaces de Sobolev. Israel J. Math. 13, 9–23.Google Scholar
[11] Cocou, M., Schryve, M. & Raous, M. (2010) A dynamic unilateral contact problem with adhesion and friction in viscoelasticity. Z. Angew. Math. Phys. 61, 721–743.Google Scholar
[12] Cocou, M. (2015) A class of dynamic contact problems with Coulomb friction in viscoelasticity. Nonlinear Anal. Real World Appl. 22, 508–519.Google Scholar
[13] Colli, P., Luterotti, F., Schimperna, G. & Stefanelli, U. (2002) Global existence for a class of generalized systems for irreversible phase changes. NoDEA Nonlinear Differ. Equ. Appl. 9, 255–276.Google Scholar
[14] Frémond, M. (2012) Phase Change in Mechanics, Springer-Verlag, Berlin, Heidelberg.Google Scholar
[15] Grun-Rehomme, M. (1977) Caractérisation du sous-différentiel d'intégrandes convexes dans les espaces de Sobolev (French). J. Math. Pures Appl. (9), 56, 149–156.Google Scholar
[16] Ioffe, A. D. (1977) On lower semicontinuity of integral functionals. I. SIAM J. Control Optim. 15, 521–538.Google Scholar
[17] Kuttler, K. L., Menike, R. S. R. & Shillor, M. (2009) Existence results for dynamic adhesive contact of a rod. J. Math. Anal. Appl. 351, 781–791.CrossRefGoogle Scholar
[18] Raous, M., Cangémi, L. & Cocu, M. (1999) A consistent model coupling adhesion, friction, and unilateral contact. Comput. Methods Appl. Mech. Eng. 177, 383–399.CrossRefGoogle Scholar
[19] Rossi, R. & Roubíček, T. (2011) Thermodynamics and analysis of rate-independent adhesive contact at small strains. Nonlinear Anal. 74, 3159–3190.CrossRefGoogle Scholar
[20] Rossi, R. & Roubíček, T. (2013) Adhesive contact delaminating at mixed mode, its thermodynamics and analysis. Interfaces Free Bound. 15, 1–37.Google Scholar
[21] Rossi, R. & Thomas, M. (2015) From an adhesive to a brittle delamination model in thermo-visco-elasticity. ESAIM Control Optim. Calc. Var. 21, 1–59.CrossRefGoogle Scholar
[22] Roubíček, T. (2005) Nonlinear Partial Differential Equations with Applications, Birkhäuser, Springer, Basel.Google Scholar
[23] Roubíček, T. (2013) Adhesive contact of visco-elastic bodies and defect measures arising by vanishing viscosity. SIAM J. Math. Anal. 45, 101–126.Google Scholar
[24] Scala, R. (2014) Limit of viscous dynamic processes in delamination as the viscosity and inertia vanish, to appear on ESAIM:COCV.Google Scholar
[25] Schimperna, G. & Pawłow, I. (2013) On a class of Cahn-Hilliard models with nonlinear diffusion. SIAM J. Math. Anal. 45, 31–63.Google Scholar
[26] Simon, J. (1987) Compact sets in the space Lp (0, T;B). Ann. Mat. Pura Appl. 146, 65–96.Google Scholar