Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T07:10:57.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of solutions of Fisher–KPP equation with free boundaries in time-periodic environment

Part of: Miscellaneous topics - Partial differential equations Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  25 March 2019

JINGJING CAI  and
LI XU
JINGJING CAI
Affiliation:
School of Mathematics and Physics, Shanghai University of Electric Power, Shanghai200090, China. emails: [email protected]; [email protected]
LI XU
Affiliation:
School of Mathematics and Physics, Shanghai University of Electric Power, Shanghai200090, China. emails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a free boundary problem of the form: ut = uxx + f(t, u) (g(t) < x < h(t)) with free boundary conditions h′(t) = −ux(t, h(t)) – α(t) and g′(t) = −ux(t, g(t)) + β(t), where β(t) and α(t) are positive T-periodic functions, f(t, u) is a Fisher–KPP type of nonlinearity and T-periodic in t. This problem can be used to describe the spreading of a biological or chemical species in time-periodic environment, where free boundaries represent the spreading fronts of the species. We study the asymptotic behaviour of bounded solutions. There are two T-periodic functions α0(t) and α*(t; β) with 0 < α0 < α* which play key roles in the dynamics. More precisely, (i) in case 0 < β< α0 and 0 < α < α*, we obtain a trichotomy result: (i-1) spreading, that is, h(t) – g(t) → +∞ and u(t, ⋅ + ct) → 1 with 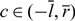$c\in (-\overline{l},\overline{r})$, where 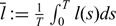$ \overline{l}:=\frac{1}{T}\int_{0}^{T}l(s)ds$, 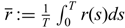$\overline{r}:=\frac{1}{T}\int_{0}^{T}r(s)ds$, the T-periodic functions −l(t) and r(t) are the asymptotic spreading speeds of g(t) and h(t) respectively (furthermore, r(t) > 0 > −l(t) when 0 < β < α < α0; r(t) = 0 > −l(t) when 0 < β < α = α0; 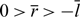$0 \gt \overline{r} \gt -\overline{l}$ when 0 < β < α0 < α < α*); (i-2) vanishing, that is, 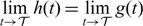$\lim\limits_{t \to \mathcal {T}}h(t) = \lim\limits_{t \to \mathcal {T}}g(t)$ and 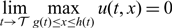$\lim\limits_{t \to \mathcal {T}}\max\limits_{g(t)\leq x\leq h(t)} u(t,x)=0$, where 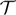$\mathcal {T}$ is some positive constant; (i-3) transition, that is, g(t) → −∞, h(t) → −∞, 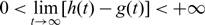$0<\lim\limits_{t \to \infty}[h(t)-g(t)] \lt +\infty$ and u(t, ⋅) → V(t, ⋅), where V is a T-periodic solution with compact support. (ii) in case β ≥ α0 or α ≥ α*, vanishing happens for any solution.

Keywords

Fisher–KPP equationfree boundary problemperiodic travelling waveasymptotic behaviour

MSC classification

Primary: 35K20: Initial-boundary value problems for second-order parabolic equations
Secondary: 35K55: Nonlinear parabolic equations 35B40: Asymptotic behavior of solutions 35R35: Free boundary problems
Type
Papers
Information
European Journal of Applied Mathematics , Volume 31 , Issue 3 , June 2020 , pp. 423 - 449
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This research was sponsored by NSFC (No. 11701359, No. 11502141).

References

Aronson, D. G. &Weinberger, H. F. (1975) Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. In: Partial Differential Equations and Related Topics, Lecture Notes in Mathematics, Vol. 446, Springer, Berlin, pp. 5–49.CrossRefGoogle Scholar
Aronson, D. G. & Weinberger, H. F. (1978) Multidimensional nonlinear diffusion arising in population genetics. Adv. Math. 30, 33–76.CrossRefGoogle Scholar
Bao, W., Du, Y., Lin, Z. G. & ZHU, H. P. (2018) Free boundary models for mosquito range movement driven by climate warming. J. Math. Biol. 76, 841–875.CrossRefGoogle ScholarPubMed
Cai, J. (2014) Asymptotic behavior of solutions of Fisher–KPP equation with free boundary conditions. Nonl. Anal. 16, 170–177.CrossRefGoogle Scholar
Cai, J. & Gu, H. (2017) Asymptotic behavior of solutions of free boundary problems for Fisher–KPP equation. Eur. J. Appl. Math. 28, 435–469.CrossRefGoogle Scholar
Cai, J., Lou, B. & Zhou, M. (2014) Asymptotic behavior of solutions of a reaction diffusion equation with free boundary conditions. J. Dyn. Diff. Equat. 26, 1007–1028.CrossRefGoogle Scholar
Cui, S. & Friedman, A. (1999) Analysis of a mathematical model of protocell, J. Math. Anal. Appl. 236, 171–206.CrossRefGoogle Scholar
Ding, W., Du, Y. & Liang, X. (2017) Spreading in space-time periodic media governed by a monostable equation with free boundaries, part 1: continuous initial functions. J. Diff. Eqns. 262, 4988–5021.CrossRefGoogle Scholar
Ding, W., Peng, R. & Wei, L. (2017) The diffusive logistic model with a free boundary in a heterogeneous time-periodic environment. J. Diff. Eqns. 263, 2736–2779.CrossRefGoogle Scholar
Du, Y. & Guo, Z. (2012) The Stefan problem for the Fisher–KPP equation. J. Diff. Eqns. 253, 996–1035.CrossRefGoogle Scholar
Du, Y., Guo, Z. & Peng, R. (2013) A diffusion logistic model with a free boundary in time-periodic environment. J. Funct. Anal. 265, 2089–2142.CrossRefGoogle Scholar
Du, Y. & Lin, Z. G. (2010) Spreading-vanishing dichotomy in the diffusive logistic model with a free boundary. SIAM J. Math. Anal. 42, 377–405.CrossRefGoogle Scholar
Du, Y. & Lou, B. (2015) Spreading and vanishing in nonlinear diffusion problems with free boundaries. J. Eur. Math. Soc. 17, 2673–2724.CrossRefGoogle Scholar
Du, Y., Lou, B. & Zhou, Z. (2015) Nonlinear diffusive problems with free boundaries: convergence, transition speed and zero number arguments. SIAM J. Math. Anal. 47, 3555–3584.CrossRefGoogle Scholar
Du, Y., Matano, H. & Wang, K. (2014) Regularity and asymptotic behavior of nonlinear Stefan problems. Arch. Ration. Mech. Anal. 212, 957–1010.CrossRefGoogle Scholar
Du, Y., Matsuzawa, H. & Zhou, M. (2014) Sharp estimate of the spreading speed determined by nonlinear free boundary problems. SIAM J. Math. Anal. 46, 375–396.CrossRefGoogle Scholar
Du, Y., Matsuzawa, H. & ZHOU, M. (2015) Spreading speed and profile for nonlinear Stefan problems in high space dimensions. J. Math. Pures Appl. 103, 741–787.CrossRefGoogle Scholar
Friedman, A. & HU, B. (1999) A Stefan problem for a protocell model. SIAM J. Math. Anal. 30, 912–926.CrossRefGoogle Scholar
Gu, H., Lou, B. & Zhou, M. (2015) Long time behavior of solutions of Fisher–KPP equation with advection and free boundaries. J. Funct. Anal. 269, 1714–1768.CrossRefGoogle Scholar
Hess, P. (1991) Periodic-parabolic boundary value problems and positivity. In: Pitman Research Notes in Mathematics, Vol. 247, Longman Scientific and Technical, Harlow.Google Scholar
Kaneko, Y.&Matsuzawa, H. (2015) Spreading speed and sharp asymptotic profiles of solutions in free boundary problems for nonlinear advection–diffusion equations. J. Math. Anal. Appl. 428, 43–76.CrossRefGoogle Scholar
Kaneko, Y. & Yamada, Y. (2011) A free boundary problem for a reaction–diffusion equation appearing in ecology. Adv. Math. Sci. Appl. 21, 467–492.Google Scholar
Li, F., Liang, X. & Shen, W. (2016) Diffusive KPP equations with free boundaries in time almost periodic environments: II. Spreading speed and semi-wave solutions. J. Diff. Eqns. 261, 2403–2445.CrossRefGoogle Scholar
Nadin, G. (2010) Existence and uniqueness of the solution of a space-time periodic reaction–diffusion equation. J. Diff. Eqns. 249, 1288–1304.CrossRefGoogle Scholar
Schwegler, H. & Tarumi, K. (1986) The protocell: a mathematical model of self-maintenance. Biosystems 19, 307–315.CrossRefGoogle ScholarPubMed
Schwegler, H., Tarumi, K. & Gerstmann, B. (1985) Physico-chemical model of a protocell. J. Math. Biol. 28, 335–348.CrossRefGoogle Scholar
Sun, N. K., Lou, B. & Zhou, M. (2017) Fisher–KPP equation with free boundaries and timeperiodic advections. Calc. Var. Partial Differ. Equ. 56, 61.CrossRefGoogle Scholar
Lou, B. & Yang, J. Spatial segregation limit of competition systems and free boundary problems, preprint.Google Scholar
Zhang, H., Qu, C. & Hu, B. (2009) Bifurcation for a free boundary problem modeling a protocell. Nonl. Anal. 70, 2779–2795.CrossRefGoogle Scholar