Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T02:15:01.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour for a non-local parabolic problem

Published online by Cambridge University Press:  01 June 2009

LIU QILIN ,
LIANG FEI  and
LI YUXIANG
LIU QILIN
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210018, Jiangsu, PR China email: [email protected] Department of Mathematics, Shanghai Jiao Tong University, Shanghai 200240, PR China
LIANG FEI
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210018, Jiangsu, PR China email: [email protected]
LI YUXIANG
Affiliation:
Department of Mathematics, Southeast University, Nanjing 210018, Jiangsu, PR China email: [email protected] Universitée Paris 13, CNRS UMR 7539, Laboratoire Analyse, Géométrie et Applications, 99, Avenue Jean-Baptiste Clément, 93430 Villetaneuse, France
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the asymptotic behaviour for the non-local parabolic problem 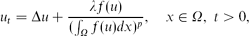with a homogeneous Dirichlet boundary condition, where λ > 0, p > 0 and f is non-increasing. It is found that (a) for 0 < p ≤ 1, u(x, t) is globally bounded and the unique stationary solution is globally asymptotically stable for any λ > 0; (b) for 1 < p < 2, u(x, t) is globally bounded for any λ > 0; (c) for p = 2, if 0 < λ < 2|∂Ω|2, then u(x, t) is globally bounded; if λ = 2|∂Ω|2, there is no stationary solution and u(x, t) is a global solution and u(x, t) → ∞ as t → ∞ for all x ∈ Ω; if λ > 2|∂Ω|2, there is no stationary solution and u(x, t) blows up in finite time for all x ∈ Ω; (d) for p > 2, there exists a λ* > 0 such that for λ > λ*, or for 0 < λ ≤ λ* and u0(x) sufficiently large, u(x, t) blows up in finite time. Moreover, some formal asymptotic estimates for the behaviour of u(x, t) as it blows up are obtained for p ≥ 2.

Type
Papers
Information
European Journal of Applied Mathematics , Volume 20 , Issue 3 , June 2009 , pp. 247 - 267
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bebernes, J. W. & Lacey, A. A. (1997) Global existence and finite time blow-up for a class of nonlocal parabolic problems. Adv. Differential Equations 2, 927–953.CrossRefGoogle Scholar
[2]Burns, T. J. (1994) Does a shear band result from a thermal explosion? Mech. Mater. 17 (2–3), 261–271.CrossRefGoogle Scholar
[3]Caglioti, E., Lions, P.-L., Marchioro, C. & Pulvirenti, M. (1992) A special class of stationary flows for two-dimensional Euler equations: A statistical mechanics description. Comm. Math. Phys. 143 (3), 501–525.CrossRefGoogle Scholar
[4]Carrillo, J. A. (1998) On a nonlocal elliptic equation with decreasing nonlinearity arising in plasma physics and heat conduction. Nonlinear Anal. 32 (1), 97–115.CrossRefGoogle Scholar
[5]Fowler, A. C., Frigaard, I. & Howison, S. D. (1992) Temperature surges in current-limiting circuit devices. SIAM J. Appl. Math. 52 (4), 998–1011.CrossRefGoogle Scholar
[6]Gilbarg, D. & Trudinger, N. S. (2001) Elliptic Partial Differential Equations of Second Order, Springer-Verlag, Berlin.CrossRefGoogle Scholar
[7]Kavallaris, N. I., Lacey, A. A. & Tzanetis, D. E. (2004) Global existence and divergence of critical solutions of a non-local parabolic problem in Ohmic heating process. Nonlinear Anal. 58 (7–8), 787–812.CrossRefGoogle Scholar
[8]Kavallaris, N. I. & Nadzieja, T. (2007) On the blow-up of the non-local thermistor problem. Proc. Edinb. Math. Soc. (2) 50 (2), 389–409.CrossRefGoogle Scholar
[9]Krzywicki, A. & Nadzieja, T. (1991) Some results concerning the Poisson–Boltzmann equation. Zastos. Mat. 21 (2), 265–272.Google Scholar
[10]Lacey, A. A. (1995) Thermal runaway in a non-local problem modelling Ohmic heating. I. Model derivation and some special cases. European J. Appl. Math. 6, 127–144.CrossRefGoogle Scholar
[11]Lacey, A. A. (1995) Thermal runaway in a non-local problem modelling Ohmic heating. II. General proof of blow-up and asymptotics of runaway. Eur. J. Appl. Math. 6, 201–224.CrossRefGoogle Scholar
[12]Olmstead, W. E., Nemat-Nasser, S. & Ni, L. (1994) Shear bands as surfaces of discontinuity. J. Mech. Phys. Solids 42, 697–709.CrossRefGoogle Scholar
[13]Sattinger, D. H. (1971/1972) Monotone methods in nonlinear elliptic and parabolic boundary value problems. Indiana Univ. Math. J. 21, 979–1000.CrossRefGoogle Scholar
[14]Tzanetis, D. M. (2002) Blow-up of radially symmetric solutions of a non-local problem modelling Ohmic heating Electron. J. Differential Equations 11, 1–26.Google Scholar