We show, by means of a perturbative weakly nonlinear analysis, that the axisymmetric magneto-rotational instability (MRI) in a magnetic Taylor-Couette (mTC) flow in a thin-gap gives rise, for very small magnetic Prandtl numbers $({\cal P}_{\rm m})$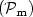, to a real Ginzburg-Landau equation for the disturbance amplitude. The saturation amplitude As is found to scale in this regime as ${\cal P}_{\rm m}^\delta$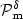, with 1/2 < δ < 2/3 (depending on the boundary conditions adopted). The asymptotic results are shown to comply with numerical calculations performed by using a spectral code. They suggest that the transport due to the nonlinearly developed MRI may be vanishingly small for ${\cal P}_{\rm m} \ll$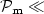 1.