A general problem with the theory of stellar tides is that the observations indicate that the effectiveness in circularising binary orbits is much larger than predicted by current theories. A mechanism that may be at least part of the solution to this problem is resonance locking: prolonged enhanced tidal interaction when the tide is nearly resonant with a stellar oscillation mode. In these lectures we focus on the dynamical tide which takes into account that the tides can indeed excite non-radial oscillations in a star when the forcing period happens to be close to the period of a free oscillation mode of the star. Such resonant interaction can in principle speed-up the tidal evolution of a close binary. By including the Coriolis force in rotating stars the oscillation spectrum is enriched by rotational oscillation modes that can also be excited by the tides. Although the chances that the tides in a particular binary system happen to be close to a resonance with a free oscillation mode seem nevertheless slim, it appears that binary systems with a significant orbital eccentricity, and thus with several tidal harmonics, evolve through many resonances on timescales short compared to their main sequence (MS) lifetime. Stellar rotation, which is usually neglected in tidal calculations, plays an important role in that it is relatively easy to tidally spin a star up or down, whereby the forcing frequency (in the stellar frame) can move towards a resonance with a free oscillation mode of the star on relatively short timescales. Often this gives rise to resonance locking whereby the system remains nearly resonant, with enhanced tidal evolution, for a relatively long period. We will present the results of several numerical simulations, for both massive MS binaries and solar type binary systems in which resonance locking is studied in some detail.Note: in the following all numerically listed frequencies are normalised by the stellar break-up speed $\Omega_c=\sqrt{G\, M_s/R^3_s}$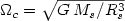, unless explicitly indicated otherwise.