Article contents
On the reduction of a random basis
Published online by Cambridge University Press: 22 September 2009
Abstract
For p ≤ n, let b1(n),...,bp(n) be independent random vectors in $\mathbb{R}^n$  with the same distribution invariant by rotation and without mass at the origin. Almost surely these vectors form a basis for the Euclidean lattice they generate. The topic of this paper is the property of reduction of this random basis in the sense of Lenstra-Lenstra-Lovász (LLL). If $\widehat b_{1}^{(n)},\ldots, \widehat b_p^{(n)}$
with the same distribution invariant by rotation and without mass at the origin. Almost surely these vectors form a basis for the Euclidean lattice they generate. The topic of this paper is the property of reduction of this random basis in the sense of Lenstra-Lenstra-Lovász (LLL). If $\widehat b_{1}^{(n)},\ldots, \widehat b_p^{(n)}$  is the basis obtained from b1(n),...,bp(n) by Gram-Schmidt orthogonalization, the quality of the reduction depends upon the sequence of ratios of squared lengths of consecutive vectors $r_j^{(n)} = \Vert \widehat b^{(n)}_{n-j+1}\Vert^2 / \Vert \widehat b^{(n)}_{n-j} \Vert^2$
is the basis obtained from b1(n),...,bp(n) by Gram-Schmidt orthogonalization, the quality of the reduction depends upon the sequence of ratios of squared lengths of consecutive vectors $r_j^{(n)} = \Vert \widehat b^{(n)}_{n-j+1}\Vert^2 / \Vert \widehat b^{(n)}_{n-j} \Vert^2$ 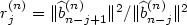 , j = 1,...,p - 1. We show that as n → +∡ the process $(r_j^{(n)}-1,j\geq 1)$
, j = 1,...,p - 1. We show that as n → +∡ the process $(r_j^{(n)}-1,j\geq 1)$ 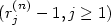 tends in distribution in some sense to an explicit process $({\mathcal R}_j -1,j\geq 1)$
tends in distribution in some sense to an explicit process $({\mathcal R}_j -1,j\geq 1)$ 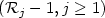 ; some properties of the latter are provided. The probability that a random random basis is s-LLL-reduced is then showed to converge for p = n - g, and g fixed, or g = g(n) → +∞.
; some properties of the latter are provided. The probability that a random random basis is s-LLL-reduced is then showed to converge for p = n - g, and g fixed, or g = g(n) → +∞.
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2009
References
- 3
- Cited by


