Published online by Cambridge University Press: 05 January 2012
In this article, we consider the stochastic heat equation $du=(\Delta u+f(t,x)){\rm d}t+ \sum_{k=1}^{\infty} g^{k}(t,x) \delta \beta_t^k, t \in [0,T]$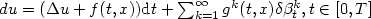 , with random coefficients f and gk,driven by a sequence (βk)k of i.i.d. fractional Brownianmotions of index H>1/2. Using the Malliavin calculus techniquesand a p-th moment maximal inequality for the infinite sum ofSkorohod integrals with respect to (βk)k, we prove that theequation has a unique solution (in a Banach space of summabilityexponent p ≥ 2), and this solution is Hölder continuous inboth time and space.
, with random coefficients f and gk,driven by a sequence (βk)k of i.i.d. fractional Brownianmotions of index H>1/2. Using the Malliavin calculus techniquesand a p-th moment maximal inequality for the infinite sum ofSkorohod integrals with respect to (βk)k, we prove that theequation has a unique solution (in a Banach space of summabilityexponent p ≥ 2), and this solution is Hölder continuous inboth time and space.