Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T15:35:11.928Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions for the distribution of M-estimates with applications to the Multi-Tone problem

Published online by Cambridge University Press:  05 January 2012

Christopher S. Withers  and
Saralees Nadarajah
Christopher S. Withers
Affiliation:
Applied Mathematics Group, Industrial Research Limited, Lower Hutt, New Zealand.
Saralees Nadarajah
Affiliation:
School of Mathematics, University of Manchester, Manchester M13 9PL, UK; [email protected]
Get access

Abstract

We give a stochastic expansion for estimates $\widehat{\theta}$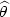that minimise the arithmetic mean of (typically independent) random functions of a known parameter θ.Examples include least squares estimates, maximum likelihood estimates and more generally M-estimates.This is used to obtain leading cumulant coefficients of $\widehat{\theta}$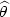needed for the Edgeworth expansions for the distribution and density n1/2 (of \widehat{\theta}$ 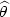− θ0) to magnitude n−3/2 (or to n−2 for the symmetric case),where θ0 is the true parameter value and n is typically the sample size.Applications are given to least squares estimates for both real and complex models.An alternative approach is given when the linear parameters of the model are nuisance parameters.The methods are illustrated with the problem of estimating the frequencieswhen the signal consists of the sum of sinusoids of unknown amplitudes.

Keywords

Biasedgeworthmaximum likelihoodM-estimatesSkewness
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 15: Supplement: In honor of Marc Yor , 2011 , pp. 139 - 167
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Booth, J.G., Hall, P. and Wood, A.T.A., On the validity of Edgeworth and saddlepoint approximations. Journal of Multivariate Analysis 51 (1994) 121–138. CrossRef
L. Comtet, Advanced Combinatorics. Reidel, Dordrecht, Holland (1974).
Gatto, R. and Ronchetti, E., General saddlepoint approximations of marginal densities and tail probabilities. Journal of the American Statistical Association 91 (1996) 666–673. CrossRef
Kakizawa, Y. and Taniguchi, M., Higher order asymptotic relation between Edgeworth approximation and saddlepoint approximation. Journal of the Japan Statistical Society 24 (1994) 109–119.
Monti, A.C., A new look at the relationship between Edgeworth expansion and saddlepoint approximation. Statistics and Probability Letters 17 (1993) 49–52. CrossRef
I.S. Reed, On a moment theorem for complex Gaussian processes. IRE Transactions on information theory IT-8 (1962) 194–195
C.S. Withers and S. Nadrajah, The bias and skewness of (univariate) M-estimates in regression. Technical Report, Applied Mathematics Group, Industrial Research Ltd., Lower Hutt, New Zealand (2007).
C.S. Withers and S. Nadarajah, Tilted Edgeworth expansions for asymptotically normal vectors. Annals of the Institute of Statistical Mathematics, doi: 10.1007/s10463-008-0206-0 (2008). CrossRef