Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T13:53:50.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic shape for the chemical distanceand first-passage percolation on the infinite Bernoulli cluster

Published online by Cambridge University Press:  15 September 2004

Olivier Garet  and
Régine Marchand
Olivier Garet
Affiliation:
Laboratoire de Mathématiques, Applications et Physique Mathématique d'Orléans UMR 6628, Université d'Orléans, BP 6759, 45067 Orléans Cedex 2, France; [email protected].
Régine Marchand
Affiliation:
Institut Elie Cartan Nancy (mathématiques), Université Henri Poincaré Nancy 1, Campus Scientifique, BP 239, 54506 Vandœuvre-lès-Nancy Cedex, France; [email protected].
Get access

Abstract

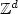The aim of this paper is to extend the well-known asymptotic shape result for first-passage percolation on $\mathbb{Z}^d$ to first-passage percolation on a random environment given by the infinite cluster of a supercritical Bernoulli percolation model. We prove the convergence of the renormalized set of wet vertices to a deterministic shape that does not depend on the realization of the infinite cluster.As a special case of our result, we obtain an asymptotic shape theorem for the chemical distance in supercritical Bernoulli percolation.We also prove a flat edge result in the case of dimension 2. Various examples are also given.

Keywords

Percolationfirst-passage percolationchemical distanceinfinite clusterasymptotic shaperandom environment.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 8 , August 2004 , pp. 169 - 199
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aizenman, M., Kesten, H. and Newman, C.M., Uniqueness of the infinite cluster and continuity of connectivity functions for short and long range percolation. Comm. Math. Phys. 111 (1987) 505–531. CrossRef
Antal, P. and Pisztora, A., On the chemical distance for supercritical Bernoulli percolation. Ann. Probab. 24 (1996) 1036–1048.
Boivin, D., First passage percolation: the stationary case. Probab. Theory Related Fields 86 (1990) 491–499. CrossRef
J.R. Brown, Ergodic theory and topological dynamics. Academic Press, Harcourt Brace Jovanovich Publishers, New York. Pure Appl. Math. 70 (1976).
Burton, R.M. and Keane, M., Density and uniqueness in percolation. Comm. Math. Phys. 121 (1989) 501–505. CrossRef
Cox, J.T., The time constant of first-passage percolation on the square lattice. Adv. Appl. Probab. 12 (1980) 864–879. CrossRef
Cox, J.T. and Durrett, R., Some limit theorems for percolation processes with necessary and sufficient conditions. Ann. Probab. 9 (1981) 583–603. CrossRef
Cox, J.T. and Kesten, H., On the continuity of the time constant of first-passage percolation. J. Appl. Probab. 18 (1981) 809–819. CrossRef
Durrett, R. and Liggett, T.M., The shape of the limit set in Richardson's growth model. Ann. Probab. 9 (1981) 186–193. CrossRef
Garet, O., Percolation transition for some excursion sets. Electron. J. Probab. 9 (2004) 255–292 (electronic). CrossRef
Häggström, O. and Meester, R., Asymptotic shapes for stationary first passage percolation. Ann. Probab. 23 (1995) 1511–1522. CrossRef
J.M. Hammersley and D.J.A. Welsh, First-passage percolation, subadditive processes, stochastic networks, and generalized renewal theory, in Proc. Internat. Res. Semin., Statist. Lab., Univ. California, Berkeley, Calif., Springer-Verlag, New York (1965) 61–110.
Kesten, H., Aspects of first passage percolation, in École d'été de probabilités de Saint-Flour, XIV–1984, Springer, Berlin. Lect. Notes Math. 1180 (1986) 125–264. CrossRef
Kesten, H. and Zhang, Y., The probability of a large finite cluster in supercritical Bernoulli percolation. Ann. Probab. 18 (1990) 537–555. CrossRef
Marchand, R., Strict inequalities for the time constant in first passage percolation. Ann. Appl. Probab. 12 (2002) 1001–1038.
Richardson, D., Random growth in a tessellation. Proc. Cambridge Philos. Soc. 74 (1973) 515–528. CrossRef
Y.G. Sinai, Introduction to ergodic theory. Princeton University Press, Princeton, N.J., Translated by V. Scheffer. Math. Notes 18 (1976).
W.F. Stout, Almost sure convergence. Academic Press, A subsidiary of Harcourt Brace Jovanovich, Publishers, New York-London. Probab. Math. Statist. 24 (1974).
van den Berg, J. and Kesten, H., Inequalities for the time constant in first-passage percolation. Ann. Appl. Probab. 3 (1993) 56–80. CrossRef