Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T05:19:32.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Positivity of the density for the stochasticwave equation in two spatial dimensions

Published online by Cambridge University Press:  15 May 2003

Mireille Chaleyat–Maurel  and
Marta Sanz–Solé
Mireille Chaleyat–Maurel
Affiliation:
Université Pierre et Marie Curie, Laboratoire de Probabilités, 175/179 rue du Chevaleret, 75013 Paris, France; and Université René Descartes, 45 rue des Saints Pères, 75006 Paris, France; [email protected].
Marta Sanz–Solé
Affiliation:
Facultat de Matemàtiques, Universitat de Barcelona, Gran Via 585, 08007 Barcelona, Spain; [email protected].
Get access

Abstract

We consider the random vector $u(t,\underlinex)=(u(t,x_1),\dots,u(t,x_d))$ 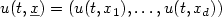, where t > 0, x1,...,xd aredistinct points of $\mathbb{R}^2$ 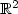and u denotes the stochastic process solution to a stochastic waveequation driven bya noise white in time and correlated in space. In a recent paper byMillet and Sanz–Solé[10], sufficient conditions are given ensuring existence andsmoothness ofdensity for $u(t,\underline x)$ 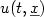. We study here the positivity of suchdensity. Usingtechniques developped in [1] (see also [9]) basedon Analysis on anabstract Wiener space, we characterize the set of points $y\in\mathbb{R}^d$ 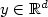where the density ispositive and we prove that, under suitable assumptions, this set is $\mathbb{R}^d$ .

Keywords

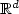Stochastic partial differential equationsMalliavin Calculuswaveequationprobability densities.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 7 , March 2003 , pp. 89 - 114
Copyright
© EDP Sciences, SMAI, 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S. Aida, S. Kusuoka and D. Stroock, On the support of Wiener functionals, edited by K.D. Elworthy and N. Ikeda, Asymptotic Problems in Probability Theory: Wiener Functionals and Asymptotics. Longman Scient. and Tech., New York, Pitman Res. Notes in Math. Ser. 284 (1993) 3-34.
Bally, V. and Pardoux, E., Malliavin Calculus for white-noise driven parabolic spde's. Potential Anal. 9 (1998) 27-64. CrossRef
Ben Arous, G. and Léandre, R., Décroissance exponentielle du noyau de la chaleur sur la diagonale (II). Probab. Theory Related Fields 90 (1991) 377-402.
Dalang, R. and Frangos, N., The stochastic wave equation in two spatial dimensions. Ann. Probab. 26 (1998) 187-212.
O. Lévêque, Hyperbolic stochastic partial differential equations driven by boundary noises. Thèse EPFL, Lausanne, 2452 (2001).
Márquez-Carreras, D., Mellouk, M. and Sarrà, M., On stochastic partial differential equations with spatially correlated noise: Smoothness of the law. Stochastic Proc. Appl. 93 (2001) 269-284. CrossRef
M. Métivier, Semimartingales. De Gruyter, Berlin (1982).
Millet, A. and Morien, P.-L., On a stochastic wave equation in two dimensions: Regularity of the solution and its density. Stochastic Proc. Appl. 86 (2000) 141-162. CrossRef
Millet, A. and Sanz-Solé, M., Points of positive density for the solution to a hyperbolic spde. Potential Anal. 7 (1997) 623-659. CrossRef
Millet, A. and Sanz-Solé, M., A stochastic wave equations in two space dimension: Smoothness of the law. Ann. Probab. 27 (1999) 803-844. CrossRef
Millet, A. and Sanz-Solé, M., Approximation and support theorem for a two space-dimensional wave equation. Bernoulli 6 (2000) 887-915. CrossRef
Morien, P.-L., Hölder and Besov regularity of the density for the solution of a white-noise driven parabolic spde. Bernoulli 5 (1999) 275-298. CrossRef
D. Nualart, Malliavin Calculus and Related Fields. Springer-Verlag (1995).
Nualart, D., Analysis on the Wiener space and anticipating calculus, in École d'été de Probabilités de Saint-Flour. Springer-Verlag, Lecture Notes in Math. 1690 (1998) 863-901.
Sanz-Solé, M. and Sarrà, M., Path properties of a class of Gaussian processes with applications to spde's, in Stochastic Processes, Physics and Geometry: New interplays, edited by F. Gesztesy et al. American Mathematical Society, CMS Conf. Proc. 28 (2000) 303-316.
Walsh, J.B., An introduction to stochastic partial differential equations, in École d'été de Probabilités de Saint-Flour, edited by P.L. Hennequin. Springer-Verlag, Lecture Notes in Math. 1180 (1986) 266-437.