Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T07:10:33.685Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of word occurrencesin a semi-Markov sequence of letters

Published online by Cambridge University Press:  21 July 2009

Margarita Karaliopoulou
Margarita Karaliopoulou*
Affiliation:
University of Athens, Department of Mathematics, 157 84 Athens, Greece; [email protected]; [email protected]
Get access

Abstract

Let a finite alphabet Ω. We consider a sequence of letters from Ωgenerated by a discrete time semi-Markov process $\{Z_{\gamma};\ \gamma\in \xN \}.$ 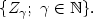Wederive the probability of a word occurrence in the sequence. We also obtain resultsfor the mean and variance of the number of overlapping occurrences of a word in afinite discrete time semi-Markov sequence of letters under certain conditions.

Keywords

Discrete time semi-Markovnumber of word occurrences
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 13 , July 2009 , pp. 328 - 342
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbu, V., Boussemart, M. and Limnios, N., Discrete time semi-Markov processes for reliability and survival analysis. Commun. Statist.-Theory and Meth. 33 (2004) 2833–2868. CrossRef
Chryssaphinou, O., Karaliopoulou, M. and Limnios, N., Discrete Time, On semi-Markov chains and applications in words occurrences. Commun. Statist.-Theory and Meth. 37 (2008) 1306–1322. CrossRef
Guibas, L.J. and Odlyzko, A.M., String Overlaps, pattern matching and nontransitive games. J. Combin. Theory Ser. A 30 (1981) 183–208. CrossRef
M. Lothaire, Combinatorics on Words. Addison-Wesley (1983).
G. Reinert, S. Schbath and M.S. Waterman, Probabilistic and Statistical Properties of Finite Words in Finite Sequences. In: Lothaire: Applied Combinatorics on Words. J. Berstel and D. Perrin (Eds.), Cambridge University Press (2005).
Stefanov, V.T., Some Waiting Time Problems, On. J. Appl. Prob. 37 (2000) 756–764. CrossRef
Stefanov, V.T., The intersite distances between pattern occurrences in strings generated by general discrete-and continuous-time models: an algorithmic approach. J. Appl. Prob. 40 (2003) 881–892. CrossRef