Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T16:40:57.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Metastable behaviour of small noise Lévy-Driven diffusions

Published online by Cambridge University Press:  25 July 2008

Peter Imkeller  and
Ilya Pavlyukevich
Peter Imkeller
Affiliation:
Institut für Mathematik, Humboldt-Universität zu Berlin, Rudower Chaussee 25, 12489 Berlin, Germany; [email protected]; [email protected]
Ilya Pavlyukevich
Affiliation:
Institut für Mathematik, Humboldt-Universität zu Berlin, Rudower Chaussee 25, 12489 Berlin, Germany; [email protected]; [email protected]
Get access

Abstract

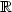We consider a dynamical system in $\mathbb{R}$ driven by a vector field -U', where U is a multi-well potential satisfying some regularity conditions. We perturb this dynamical system by a Lévy noise of small intensity and such that the heaviest tail of its Lévy measure is regularly varying. We show that the perturbed dynamical system exhibits metastable behaviour i.e. on a proper time scale it reminds of a Markov jump process taking values in the local minima of the potential U. Due to the heavy-tailnature of the random perturbation, the results differ strongly from the well studied purely Gaussian case.

Keywords

Lévy processjump diffusionheavy tailregular variationmetastabilityextreme eventsfirst exit timelarge deviations
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 12 , 2008 , pp. 412 - 437
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

N.H. Bingham, C.M. Goldie and J.L. Teugels, Regular variation, Encyclopedia of Mathematics and its applications 27. Cambridge University Press, Cambridge (1987).
Bovier, A., Eckhoff, M., Gayrard, V., and Klein, M., Metastability in reversible diffusion processes I: Sharp asymptotics for capacities and exit times. Eur. Math. Soc. 6 (2004) 399–424. CrossRef
Bovier, A., Gayrard, V. and Klein, M., Metastability in reversible diffusion processes II: Precise asymptotics for small eigenvalues. Eur. Math. Soc. 7 (2005) 69–99. CrossRef
Buslov, V.A. and Makarov, K.A., Life times and lower eigenvalues of an operator of small diffusion. Matematicheskie Zametki 51 (1992) 20–31.
S. Cerrai, Second order PDE's in finite and infinite dimension. A probabilistic approach. Lect. Notes Math. Springer, Berlin Heidelberg (2001).
Chechkin, A.V., Gonchar, V.Yu, Klafter, J. and Metzler, R., Barrier crossings of a Lévy flight. EPL 72 (2005) 348–354. CrossRef
On, M.V. Day the exponential exit law in the small parameter exit problem. Stochastics 8 (1983) 297–323.
Ditlevsen, P.D., Anomalous jumping in a double-well potential. Phys. Rev. E 60 (1999) 172–179. CrossRef
Ditlevsen, P.D., Observation of α-stable noise induced millenial climate changes from an ice record. Geophysical Research Letters 26 (1999) 1441–1444. CrossRef
M.I. Freidlin and A.D. Wentzell, Random perturbations of dynamical systems, Grundlehren der Mathematischen Wissenschaften 260. Springer, New York, NY, second edition (1998).
Galves, A., Olivieri, E. and Vares, M.E., Metastability for a class of dynamical systems subject to small random perturbations. Ann. Probab. 15 (1987) 1288–1305. CrossRef
Godovanchuk, V.V., Asymptotic probabilities of large deviations due to large jumps of a Markov process. Theory Probab. Appl. 26 (1982) 314–327. CrossRef
Imkeller, P. and Pavlyukevich, I., First exit times of SDEs driven by stable Lévy processes. Stochastic Process. Appl. 116 (2006) 611–642. CrossRef
O. Kallenberg, Foundations of modern probability. Probability and Its Applications. Springer, second edition (2002).
Kipnis, C. and Newman, C.M., The metastable behavior of infrequently observed, weakly random, one-dimensional diffusion processes. SIAM J. Appl. Math. 45 (1985) 972–982. CrossRef
Kolokol'tsov, V.N. and Makarov, K.A., Asymptotic spectral analysis of a small diffusion operator and the life times of the corresponding diffusion process. Russian J. Math. Phys. 4 (1996) 341–360.
P. Mathieu, Spectra, exit times and long time asymptotics in the zero-white-noise limit. Stoch. Stoch. Rep. 55 1–20 (1995).
Ph.E. Protter, Stochastic integration and differential equations, Applications of Mathematics 21. Springer, Berlin, second edition (2004).
Samorodnitsky, G. and Grigoriu, M., Tails of solutions of certain nonlinear stochastic differential equations driven by heavy tailed Lévy motions. Stoch. Process. Appl. 105 (2003) 69–97. CrossRef
A.D. Wentzell, Limit theorems on large deviations for Markov stochastic processes, Mathematics and Its Applications (Soviet Series) 38 . Kluwer Academic Publishers, Dordrecht (1990).
Williams, M., Asymptotic exit time distributions. SIAM J. Appl. Math. 42 (1982) 149–154. CrossRef
Ai H. Xia, Weak convergence of jump processes, in Séminaire de Probabilités, XXVI, Lect. Notes Math. 1526 Springer, Berlin (1992) 32–46.