Article contents
Local limit theorems for Brownian additive functionalsand penalisation of Brownian paths, IX
Published online by Cambridge University Press: 15 December 2008
Abstract
We obtain a local limit theorem for the laws of a class of Brownian additive functionals and we apply this result to a penalisation problem. We study precisely the case of the additive functional: $(A_t^{-}:= \int_0^t 1_{X_s < 0}{\rm d}s, t\geq 0)$ 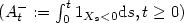 . On the other hand, we describe Feynman-Kac type penalisation results for long Brownian bridges thus completing some similar previous study for standard Brownian motion (see [B. Roynette, P. Vallois and M. Yor, Studia Sci. Math. Hung.43 (2006) 171–246]).
. On the other hand, we describe Feynman-Kac type penalisation results for long Brownian bridges thus completing some similar previous study for standard Brownian motion (see [B. Roynette, P. Vallois and M. Yor, Studia Sci. Math. Hung.43 (2006) 171–246]).
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2010
References
- 1
- Cited by


