Published online by Cambridge University Press: 15 August 2002
We consider a generalization of the so-called divide andcolor model recently introduced by Häggström. We investigate thebehavior of the magnetization in large boxes of the lattice $\mathbb{Z}^d$ 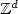 and its fluctuations. Thus, Laws of Large Numbers and CentralLimit Theorems are proved, both quenched and annealed. We showthat the properties of the underlying percolation process deeplyinfluence the behavior of the coloring model. In the subcriticalcase, the limit magnetization is deterministic and the CentralLimit Theorem admits a Gaussian limit. Conversely, the limitmagnetization is not deterministic in the supercritical case andthe limit of the Central Limit Theorem is not Gaussian, except inthe particular model with exactly two colors which are equallyprobable. We also prove a Central Limit Theorem for the size of the intersection of the infinite cluster with large boxes in supercritical bond percolation.
and its fluctuations. Thus, Laws of Large Numbers and CentralLimit Theorems are proved, both quenched and annealed. We showthat the properties of the underlying percolation process deeplyinfluence the behavior of the coloring model. In the subcriticalcase, the limit magnetization is deterministic and the CentralLimit Theorem admits a Gaussian limit. Conversely, the limitmagnetization is not deterministic in the supercritical case andthe limit of the Central Limit Theorem is not Gaussian, except inthe particular model with exactly two colors which are equallyprobable. We also prove a Central Limit Theorem for the size of the intersection of the infinite cluster with large boxes in supercritical bond percolation.