Article contents
Lifetime asymptotics of iterated Brownian motion in $\mathbb{R}^{n}$ 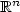
Published online by Cambridge University Press: 31 March 2007
Abstract
Let $\tau _{D}(Z) $ 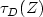 be the first exit time ofiterated Brownian motion from a domain $D \subset \mathbb{R}^{n}$
be the first exit time ofiterated Brownian motion from a domain $D \subset \mathbb{R}^{n}$ 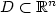 started at $z\in D$
started at $z\in D$ 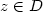 and let $P_{z}[\tau _{D}(Z)>t]$
and let $P_{z}[\tau _{D}(Z)>t]$ 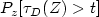 be itsdistribution. In this paper we establish the exact asymptotics of $P_{z}[\tau _{D}(Z)>t]$
be itsdistribution. In this paper we establish the exact asymptotics of $P_{z}[\tau _{D}(Z)>t]$ 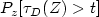 over bounded domains as an improvement of the results in DeBlassie (2004) [DeBlassie, Ann. Appl. Prob.14 (2004) 1529–1558] and Nane (2006) [Nane, Stochastic Processes Appl.116(2006) 905–916], for $z\in D$
over bounded domains as an improvement of the results in DeBlassie (2004) [DeBlassie, Ann. Appl. Prob.14 (2004) 1529–1558] and Nane (2006) [Nane, Stochastic Processes Appl.116(2006) 905–916], for $z\in D$ 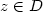 $ \displaystyle \lim_{t\to\infty}t^{-1/2}\exp\left(\frac{3}{2}\pi^{2/3}\lambda_{D}^{2/3}t^{1/3}\right)P_{z}[\tau_{D}(Z)>t]= C(z),\nonumber$
$ \displaystyle \lim_{t\to\infty}t^{-1/2}\exp\left(\frac{3}{2}\pi^{2/3}\lambda_{D}^{2/3}t^{1/3}\right)P_{z}[\tau_{D}(Z)>t]= C(z),\nonumber$ 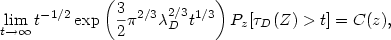 where $C(z)=(\lambda_{D}2^{7/2})/\sqrt{3 \pi}\left(\psi(z)\int_{D}\psi(y){\rm d}y\right) ^{2}$
where $C(z)=(\lambda_{D}2^{7/2})/\sqrt{3 \pi}\left(\psi(z)\int_{D}\psi(y){\rm d}y\right) ^{2}$ 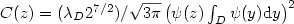 . Here λD is thefirst eigenvalue of the Dirichlet Laplacian $\frac{1}{2}\Delta$
. Here λD is thefirst eigenvalue of the Dirichlet Laplacian $\frac{1}{2}\Delta$ 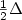 inD, and ψ is the eigenfunction corresponding toλD . We also study lifetime asymptotics of Brownian-time Brownian motion, $Z^{1}_{t} = z+X(|Y(t)|)$
inD, and ψ is the eigenfunction corresponding toλD . We also study lifetime asymptotics of Brownian-time Brownian motion, $Z^{1}_{t} = z+X(|Y(t)|)$ 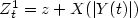 , where X t and Y t are independentone-dimensional Brownian motions, in several unbounded domains. Using these results we obtain partial results for lifetime asymptotics of iterated Brownian motion in these unbounded domains.
, where X t and Y t are independentone-dimensional Brownian motions, in several unbounded domains. Using these results we obtain partial results for lifetime asymptotics of iterated Brownian motion in these unbounded domains.
Keywords
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2007
References
- 7
- Cited by


