Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T08:10:03.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations for independent random variables – Application to Erdös-Renyi's functional law of large numbers

Published online by Cambridge University Press:  15 November 2005

Jamal Najim
Jamal Najim*
Affiliation:
CNRS, École Nationale Supérieure des Télécommunications, 46 rue Barrault 75634 Paris Cedex 13, France; [email protected]
Get access

Abstract

A Large Deviation Principle (LDP) is proved for the family $\frac{1}{n}\sum_1^n\mathbf{f}(x_i^n) \cdot Z^n_i$ 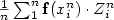where the deterministic probability measure $\frac{1}{n}\sum_1^n \delta_{x_i^n}$ 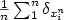converges weakly to a probability measure R and $(Z^n_i)_{i\in \mathbb{N}}$ 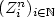are $\mathbb{R}^d$ 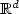-valued independent random variables whose distribution depends on $x_i^n$ 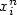and satisfies the following exponential moments condition: $$ \sup_{i,n} {\mathbb E}{\rm e}^{\alpha^* |Z_i^n|}< +\infty \quad\textrm{for some}\quad 0<\alpha^*<+\infty.$$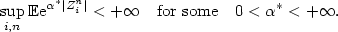

In this context, the identification of the rate function is non-trivial due to the absence of equidistribution. We rely on fine convex analysis to address this issue. Among the applications of this result, we extend Erdös and Rényi's functional law of large numbers.

Keywords

Large deviationsepigraphical convergenceErdös-Rényi's law of large numbers.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 9 , February 2005 , pp. 116 - 142
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben Arous, G., Dembo, A. and Guionnet, A., Aging of spherical spin glasses. Probab. Theory Related Fields 120 (2001) 1–67. CrossRef
Borovkov, K.A., The functional form of the Erdős-Rényi law of large numbers. Teor. Veroyatnost. i Primenen. 35 (1990) 758–762.
Chi, Z., The first-order asymptotic of waiting times with distortion between stationary processes. IEEE Trans. Inform. Theory 47 (2001) 338–347.
Chi, Z., Stochastic sub-additivity approach to the conditional large deviation principle. Ann. Probab. 29 (2001) 1303–1328. CrossRef
Csiszár, I., Sanov property, generalized I-projection and a conditionnal limit theorem. Ann. Probab. 12 (1984) 768–793. CrossRef
Dawson, D.A. and Gärtner, J., Multilevel large deviations and interacting diffusions. Probab. Theory Related Fields 98 (1994) 423–487. CrossRef
D.A. Dawson and J. Gärtner, Analytic aspects of multilevel large deviations, in Asymptotic methods in probability and statistics (Ottawa, ON, 1997). North-Holland, Amsterdam (1998) 401–440.
Deheuvels, P., Functional Erdős-Rényi laws. Studia Sci. Math. Hungar. 26 (1991) 261–295.
Dembo, A. and Kontoyiannis, I., The asymptotics of waiting times between stationary processes, allowing distortion. Ann. Appl. Probab. 9 (1999) 413–429.
Dembo, A. and Zajic, T., Large deviations: from empirical mean and measure to partial sums process. Stochastic Process. Appl. 57 (1995) 191–224. CrossRef
A. Dembo and O. Zeitouni, Large Deviations Techniques And Applications. Springer-Verlag, New York, second edition (1998).
J. Dieudonné, Calcul infinitésimal. Hermann, Paris (1968).
Djellout, H., Guillin, A. and Large, L. Wu and moderate deviations for quadratic empirical processes. Stat. Inference Stoch. Process. 2 (1999) 195–225. CrossRef
R.M. Dudley, Real Analysis and Probability. Wadsworth and Brooks/Cole (1989).
Ellis, R.S., Gough, J. and Pulé, J.V., The large deviation principle for measures with random weights. Rev. Math. Phys. 5 (1993) 659–692. CrossRef
Erdős, P. and Rényi, A., On a new law of large numbers. J. Anal. Math. 23 (1970) 103–111. CrossRef
Gamboa, F. and Gassiat, E., Bayesian methods and maximum entropy for ill-posed inverse problems. Ann. Statist. 25 (1997) 328–350.
Gantert, N., Functional Erdős-Renyi laws for semiexponential random variables. Ann. Probab. 26 (1998) 1356–1369.
Högnäs, G., Characterization of weak convergence of signed measures on [0,1]. Math. Scand. 41 (1977) 175–184. CrossRef
Léonard, C. and Najim, J., An extension of Sanov's theorem: application to the Gibbs conditioning principle. Bernoulli 8 (2002) 721–743.
Lynch, J. and Sethuraman, J., Large deviations for processes with independent increments. Ann. Probab. 15 (1987) 610–627. CrossRef
Najim, J., Cramér, A type theorem for weighted random variables. Electron. J. Probab. 7 (2002) 32 (electronic). CrossRef
R.T. Rockafellar, Convex Analysis. Princeton University Press, Princeton (1970).
Rockafellar, R.T., Integrals which are convex functionals, II. Pacific J. Math. 39 (1971) 439–469. CrossRef
R.T. Rockafellar and R.J-B. Wets, Variational Analysis. Springer (1998).
Sanchis, G.R., Addendum: “A functional limit theorem for Erdős and Rényi's law of large numbers”. Probab. Theory Related Fields 99 (1994) 475. CrossRef
Sanchis, G.R., A functional limit theorem for Erdős and Rényi's law of large numbers. Probab. Theory Related Fields 98 (1994) 1–5. CrossRef
Schuette, P.H., Large deviations for trajectories of sums of independent random variables. J. Theoret. Probab. 7 (1994) 3–45. CrossRef
S.L. Zabell, Mosco convergence and large deviations, in Probability in Banach spaces, 8 (Brunswick, ME, 1991). Birkhäuser Boston, Boston, MA, Progr. Probab. 30 (1992) 245–252.