Article contents
Hölderian invariance principle for Hilbertian linear processes
Published online by Cambridge University Press: 04 July 2009
Abstract
Let $(\xi_n)_{n\ge 1}$ 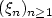 be the polygonal partial sums processes built on the linear processes $X_n=\sum_{i\ge 0}a_i(\epsilon_{n-i})$
be the polygonal partial sums processes built on the linear processes $X_n=\sum_{i\ge 0}a_i(\epsilon_{n-i})$ 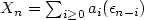 , n ≥ 1, where $(\epsilon_i)_{i\in\mathbb{Z}}$
, n ≥ 1, where $(\epsilon_i)_{i\in\mathbb{Z}}$ 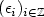 are i.i.d., centered random elements in some separable Hilbert space $\mathbb{H}$
are i.i.d., centered random elements in some separable Hilbert space $\mathbb{H}$ 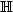 and the a i 's are bounded linear operators $\mathbb{H}\to \mathbb{H}$
and the a i 's are bounded linear operators $\mathbb{H}\to \mathbb{H}$ 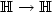 , with $\sum_{i\ge 0}\lVert a_i\rVert<\infty$
, with $\sum_{i\ge 0}\lVert a_i\rVert<\infty$ 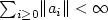 . We investigate functional central limit theorem for $\xi_n$
. We investigate functional central limit theorem for $\xi_n$ 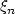 in the Hölder spaces $\mathrm{H}^o_\rho(\mathbb{H})$
in the Hölder spaces $\mathrm{H}^o_\rho(\mathbb{H})$ 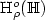 of functions $x:[0,1]\to\mathbb{H}$
of functions $x:[0,1]\to\mathbb{H}$ 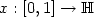 such that ||x(t + h) - x(t)|| = o(p(h)) uniformly in t, where p(h) = hαL(1/h), 0 ≤ h ≤ 1 with 0 ≤ α ≤ 1/2 and L slowly varying at infinity. We obtain the $\mathrm{H}^o_\rho(\mathbb{H})$
such that ||x(t + h) - x(t)|| = o(p(h)) uniformly in t, where p(h) = hαL(1/h), 0 ≤ h ≤ 1 with 0 ≤ α ≤ 1/2 and L slowly varying at infinity. We obtain the $\mathrm{H}^o_\rho(\mathbb{H})$ 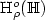 weak convergence of $\xi_n$
weak convergence of $\xi_n$ 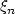 to some $\mathbb{H}$
to some $\mathbb{H}$ 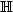 valued Brownian motion under the optimal assumption that for any c>0, $tP(\lVert \epsilon_0\rVert>ct^{1/2}\rho(1/t))=o(1)$
valued Brownian motion under the optimal assumption that for any c>0, $tP(\lVert \epsilon_0\rVert>ct^{1/2}\rho(1/t))=o(1)$ 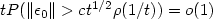 when t tends to infinity, subject to some mild restriction on L in the boundary case α = 1/2. Our result holds in particular with the weight functions p(h) = h1/2 lnβ(1/h), β > 1/2>.
when t tends to infinity, subject to some mild restriction on L in the boundary case α = 1/2. Our result holds in particular with the weight functions p(h) = h1/2 lnβ(1/h), β > 1/2>.
Keywords
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2009
References
- 2
- Cited by


