Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aoki, Kazuo
Tsuji, Tetsuro
and
Cavallaro, Guido
2009.
Approach to steady motion of a plate moving in a free-molecular gas under a constant external force.
Physical Review E,
Vol. 80,
Issue. 1,
Buttà, Paolo
Ferrari, Giorgio
and
Marchioro, Carlo
2010.
Speedy Motions of a Body Immersed in an Infinitely Extended Medium.
Journal of Statistical Physics,
Vol. 140,
Issue. 6,
p.
1182.
CAVALLARO, GUIDO
and
MARCHIORO, CARLO
2010.
ON THE APPROACH TO EQUILIBRIUM FOR A PENDULUM IMMERSED IN A STOKES FLUID.
Mathematical Models and Methods in Applied Sciences,
Vol. 20,
Issue. 11,
p.
1999.
Tsuji, Tetsuro
Aoki, Kazuo
and
Golse, François
2010.
Relaxation of a Free-Molecular Gas to Equilibrium Caused by Interaction with Vessel Wall.
Journal of Statistical Physics,
Vol. 140,
Issue. 3,
p.
518.
Cavallaro, Guido
Marchioro, Carlo
and
Tsuji, Tetsuro
2011.
Approach to equilibrium of a rotating sphere in a Stokes flow.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 57,
Issue. 2,
p.
211.
Tsuji, Tetsuro
and
Aoki, Kazuo
2012.
Decay of a Linear Pendulum in a Free-Molecular Gas and in a Special Lorentz Gas.
Journal of Statistical Physics,
Vol. 146,
Issue. 3,
p.
620.
Cavallaro, Guido
and
Marchioro, Carlo
2012.
On the Motion of an Elastic Body in a Free Gas.
Reports on Mathematical Physics,
Vol. 69,
Issue. 2,
p.
251.
Salvarani, Francesco
2013.
On the linear Boltzmann equation in evolutionary domains with an absorbing boundary.
Journal of Physics A: Mathematical and Theoretical,
Vol. 46,
Issue. 35,
p.
355501.
Tsuji, Tetsuro
and
Aoki, Kazuo
2013.
Moving boundary problems for a rarefied gas: Spatially one-dimensional case.
Journal of Computational Physics,
Vol. 250,
Issue. ,
p.
574.
Sisti, Francesco
and
Ricciuti, Costantino
2014.
Effects of Concavity on the Motion of a Body Immersed in a Vlasov Gas.
SIAM Journal on Mathematical Analysis,
Vol. 46,
Issue. 6,
p.
3579.
Tsuji, Tetsuro
and
Aoki, Kazuo
2014.
Decay of a linear pendulum in a collisional gas: Spatially one-dimensional case.
Physical Review E,
Vol. 89,
Issue. 5,
Chen, Xuwen
and
Strauss, Walter
2014.
Approach to Equilibrium of a Body Colliding Specularly and Diffusely with a Sea of Particles.
Archive for Rational Mechanics and Analysis,
Vol. 211,
Issue. 3,
p.
879.
Tsuji, Tetsuro
Arai, Junichi
and
Kawano, Satoyuki
2015.
Slow approach to steady motion of a concave body in a free-molecular gas.
Physical Review E,
Vol. 92,
Issue. 1,
Buttà, Paolo
Cavallaro, Guido
and
Marchioro, Carlo
2015.
Mathematical Models of Viscous Friction.
Vol. 2135,
Issue. ,
p.
63.
Chen, Xuwen
and
Strauss, Walter
2015.
Velocity Reversal Criterion of a Body Immersed in a Sea of Particles.
Communications in Mathematical Physics,
Vol. 338,
Issue. 1,
p.
139.
Chen, Xuwen
and
Strauss, Walter A.
2015.
Convergence to Equilibrium of a Body Moving in a Kinetic Sea.
SIAM Journal on Mathematical Analysis,
Vol. 47,
Issue. 6,
p.
4630.
Fanelli, Cristiano
Sisti, Francesco
and
Stagno, Gabriele V.
2016.
Time dependent friction in a free gas.
Journal of Mathematical Physics,
Vol. 57,
Issue. 3,
Koike, Kai
2018.
Motion of a Rigid Body in a Special Lorentz Gas: Loss of Memory Effect.
Journal of Statistical Physics,
Vol. 172,
Issue. 3,
p.
795.
Iatcenko, Anton
and
Sun, Weiran
2020.
Uniqueness of Solutions to a Gas-Disk Interaction System.
Archive for Rational Mechanics and Analysis,
Vol. 235,
Issue. 3,
p.
2027.
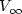 and prove that, under suitable smallness assumptions, the approach to equilibrium is $$|V(t)-V_\infty|\approx \frac{C}{t^{d+1}},$$
and prove that, under suitable smallness assumptions, the approach to equilibrium is $$|V(t)-V_\infty|\approx \frac{C}{t^{d+1}},$$ 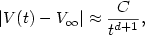 where d is the dimension of the space, and C is a positive constant. This approach is not exponential, as typical in friction problems, and even slower than for the same problem with elastic collisions.
where d is the dimension of the space, and C is a positive constant. This approach is not exponential, as typical in friction problems, and even slower than for the same problem with elastic collisions.