Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T02:58:08.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical analysis of the planewave discretization of some orbital-free and Kohn-Sham models

Published online by Cambridge University Press:  24 October 2011

Eric Cancès ,
Rachida Chakir  and
Yvon Maday
Eric Cancès
Affiliation:
Université Paris-Est, CERMICS, Project-team Micmac, INRIA-École des Ponts, 6 & 8 avenue Blaise Pascal, 77455 Marne-la-Vallée Cedex 2, France. [email protected]
Rachida Chakir
Affiliation:
UPMC Univ. Paris 06, UMR 7598 LJLL, 75005 Paris, France CNRS, UMR 7598 LJLL, 75005 Paris, France
Yvon Maday
Affiliation:
UPMC Univ. Paris 06, UMR 7598 LJLL, 75005 Paris, France CNRS, UMR 7598 LJLL, 75005 Paris, France Division of Applied Mathematics, 182 George Street, Brown University, Providence, RI 02912, USA

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this article, we provide a priori error estimates for the spectral andpseudospectral Fourier (also called planewave) discretizations of theperiodic Thomas-Fermi-von Weizsäcker (TFW) model and for the spectraldiscretization of the periodic Kohn-Shammodel, within the local density approximation (LDA). These modelsallow to compute approximations of the electronic ground state energy and densityof molecular systems in the condensed phase. The TFW model is strictlyconvex with respect to the electronic density, and allows for acomprehensive analysis. This is not the case for the Kohn-Sham LDAmodel, for which the uniqueness of the ground state electronic densityis not guaranteed. 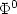We prove that, for any local minimizer $\Phi^0$ of the Kohn-Sham LDA model, and under a coercivity assumption ensuring the local uniqueness of this minimizer up to unitary transform, the discretized Kohn-Sham LDA problem has a minimizer in the vicinity of $\Phi^0$ 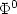for large enough energy cut-offs, and that this minimizer is unique up to unitary transform. We then derive optimal a priori error estimates for the spectral discretization method.

Keywords

Electronic structure calculationdensity functional theoryThomas-Fermi-von Weizsäcker modelKohn-Sham modelnonlinear eigenvalue problemspectral methods
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 46 , Issue 2 , March 2012 , pp. 341 - 388
Copyright
© EDP Sciences, SMAI, 2011

References

Anantharaman, A. and Cancès, E., Existence of minimizers for Kohn-Sham models in quantum chemistry. Ann. Inst. Henri Poincaré 26 (2009) 2425–2455. CrossRef
Benguria, R., Brezis, H. and Lieb, E.H., The Thomas-Fermi-von Weizsäcker theory of atoms and molecules. Comm. Math. Phys. 79 (1981) 167–180. CrossRef
Blanc, X. and Cancès, E., Nonlinear instability of density-independent orbital-free kinetic energy functionals. J. Chem. Phys. 122 (2005) 214–106. CrossRef
Born, M. and Oppenheimer, J.R., Zur quantentheorie der molekeln. Ann. Phys. 84 (1927) 457–484. CrossRef
Bourdaud, G. and Lanza de, M. Cristoforis, Regularity of the symbolic calculus in Besov algebras. Stud. Math. 184 (2008) 271–298. CrossRef
Cancès, E., Chakir, R. and Maday, Y., Numerical analysis of nonlinear eigenvalue problems. J. Sci. Comput. 45 (2010) 90–117. CrossRef
E. Cancès, R. Chakir, V. Ehrlacher and Y. Maday, in preparation.
E. Cancès, M. Defranceschi, W. Kutzelnigg, C. Le Bris and Y. Maday, Computational quantum chemistry: a primer, in Handbook of numerical analysis X. North-Holland, Amsterdam (2003) 3–270. CrossRef
E. Cancès, C. Le Bris and Y. Maday, Méthodes mathématiques en chimie quantique. Springer (2006).
Cancès, E., Stoltz, G., Staroverov, V.N., Scuseria, G.E. and Davidson, E.R., Local exchange potentials for electronic structure calculations. MathematicS In Action 2 (2009) 1–42. CrossRef
C. Canuto, M.Y. Hussaini, A. Quarteroni and T.A. Zang, Spectral methods: fundamentals in single domains. Springer (2006).
I. Catto, C. Le Bris and P.-L. Lions, Mathematical theory of thermodynamic limits: Thomas-Fermi type models. Oxford University Press (1998).
H. Chen, X. Gong, L. He and A. Zhou, Convergence of adaptive finite element approximations for nonlinear eigenvalue problems. arXiv preprint, http://arxiv.org/pdf/1001.2344.
Chen, H., Gong, X. and Zhou, A., Numerical approximations of a nonlinear eigenvalue problem and applications to a density functional model. Math. Methods Appl. Sci. 33 (2010) 1723–1742. CrossRef
R.M. Dreizler and E.K.U. Gross, Density functional theory. Springer (1990).
Edelman, A., Arias, T.A. and Smith, S.T., The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl. 20 (1998) 303–353. CrossRef
Gavini, V., Knap, J., Bhattacharya, K. and Ortiz, M., Non-periodic finite-element formulation of orbital-free density functional theory. J. Mech. Phys. Solids 55 (2007) 669–696. CrossRef
D. Gilbarg and N.S. Trudinger, Elliptic partial differential equations of second order, 3rd edition. Springer (1998).
Gonze, X. et al., ABINIT: first-principles approach to material and nanosystem properties. Computer Phys. Comm. 180 (2009) 2582–2615. CrossRef
Hohenberg, P. and Kohn, W., Inhomogeneous electron gas. Phys. Rev. 136 (1964) B864–B871. CrossRef
Kohn, W. and Sham, L.J., Self-consistent equations including exchange and correlation effects. Phys. Rev. 140 (1965) A1133–A1138. CrossRef
Langwallner, B., Ortner, C. and Süli, E., Existence and convergence results for the Galerkin approximation of an electronic density functional. Math. Mod. Methods Appl. Sci. 20 (2010) 2237–2265. CrossRef
C. Le Bris, Ph.D. thesis, École Polytechnique (1993).
W.A. Lester Jr. Ed., Recent advances in Quantum Monte Carlo methods. World Sientific (1997).
W.A. Lester Jr., S.M. Rothstein and S. Tanaka Eds., Recent advances in Quantum Monte Carlo methods, Part II, World Sientific (2002).
Levy, M., Universal variational functionals of electron densities, first order density matrices, and natural spin-orbitals and solution of the V-representability problem. Proc. Natl. Acad. Sci. U.S.A. 76 (1979) 6062–6065. CrossRef
Lieb, E.H., Thomas-Fermi and related theories of atoms and molecules. Rev. Mod. Phys. 53 (1981) 603–641. CrossRef
Lieb, E.H., Density Functional for Coulomb systems. Int. J. Quant. Chem. 24 (1983) 243–277. CrossRef
Maday, Y. and Turinici, G., Error bars and quadratically convergent methods for the numerical simulation of the Hartree-Fock equations. Numer. Math. 94 (2003) 739–770. CrossRef
Sickel, W., Superposition of functions in Sobolev spaces of fractional order. A survey. Banach Center Publ. 27 (1992) 481–497. CrossRef
Suryanarayana, P., Gavini, V., Blesgen, T., Bhattacharya, K. and Ortiz, M., Non-periodic finite-element formulation of Kohn-Sham density functional theory. J. Mech. Phys. Solids 58 (2010) 256–280. CrossRef
Troullier, N. and Martins, J.L., A straightforward method for generating soft transferable pseudopotentials. Solid State Commun. 74 (1990) 613–616. CrossRef
Valone, S., Consequences of extending 1matrix energy functionals from purestate representable to all ensemble representable 1 matrices. J. Chem. Phys. 73 (1980) 1344–1349. CrossRef
Y.A. Wang and E.A. Carter, Orbital-free kinetic energy density functional theory, in Theoretical methods in condensed phase chemistry, Progress in theoretical chemistry and physics 5. Kluwer (2000) 117–184.
Zhou, A., Finite dimensional approximations for the electronic ground state solution of a molecular system. Math. Methods Appl. Sci. 30 (2007) 429–447. CrossRef