This paper is concerned with the dual formulation of the interface problemconsisting of a linear partial differential equation with variable coefficientsin some bounded Lipschitz domain Ω in $\mathbb{R}^n$ 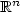(n ≥ 2) and the Laplace equation with some radiation condition in theunbounded exterior domain Ωc := $\mathbb{R}^n\backslash\bar\Omega$ 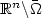. The two problems are coupled by transmission andSignorini contact conditions on the interface Γ = ∂Ω. The exterior part of theinterface problem is rewritten using a Neumann to Dirichlet mapping (NtD) given in terms of boundary integral operators. The resulting variational formulation becomes a variational inequalitywith a linear operator. Then we treat the corresponding numerical scheme and discuss anapproximation of the NtD mapping with an appropriatediscretization of the inverse Poincaré-Steklov operator. In particular, assuming some abstract approximationproperties and a discrete inf-sup condition, we show unique solvability of the discrete scheme andobtain the corresponding a-priori error estimate. Next, we prove that these assumptions aresatisfied with Raviart-Thomas elements and piecewise constants in Ω, and continuous piecewise linear functions on Γ. We suggest a solver based on a modified Uzawa algorithm and show convergence. Finally we present some numerical results illustrating our theory.