Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Machmoum, A.
and
Esselaoui, D.
2001.
Finite element approximation of viscoelastic fluid flow using characteristics method.
Computer Methods in Applied Mechanics and Engineering,
Vol. 190,
Issue. 42,
p.
5603.
Bermúdez, Alfredo
Nogueiras, Maria R.
and
Vázquez, Carlos
2006.
Numerical Analysis of Convection‐Diffusion‐Reaction Problems with Higher Order Characteristics/Finite Elements. Part I: Time Discretization.
SIAM Journal on Numerical Analysis,
Vol. 44,
Issue. 5,
p.
1829.
Bermúdez, Alfredo
Nogueiras, Maria R.
and
Vázquez, Carlos
2006.
Numerical Analysis of Convection‐Diffusion‐Reaction Problems with Higher Order Characteristics/Finite Elements. Part II: Fully Discretized Scheme and Quadrature Formulas.
SIAM Journal on Numerical Analysis,
Vol. 44,
Issue. 5,
p.
1854.
García, M. Benítez
Rebollo, T. Chacón
Mármol, M. Gómez
and
Narbona-Reina, G.
2011.
BAIL 2010 - Boundary and Interior Layers, Computational and Asymptotic Methods.
Vol. 81,
Issue. ,
p.
21.
Benítez, M.
and
Bermúdez, A.
2011.
A second order characteristics finite element scheme for natural convection problems.
Journal of Computational and Applied Mathematics,
Vol. 235,
Issue. 11,
p.
3270.
Benítez, Marta
and
Bermúdez, Alfredo
2012.
Numerical Analysis of a Second order Pure Lagrange–Galerkin Method for Convection-Diffusion Problems. Part I: Time Discretization.
SIAM Journal on Numerical Analysis,
Vol. 50,
Issue. 2,
p.
858.
2012.
Equity Hybrid Derivatives.
p.
313.
Benítez, Marta
and
Bermúdez, Alfredo
2012.
Numerical Analysis of a Second Order Pure Lagrange--Galerkin Method for Convection-Diffusion Problems. Part II: Fully Discretized Scheme and Numerical Results.
SIAM Journal on Numerical Analysis,
Vol. 50,
Issue. 6,
p.
2824.
Heumann, Holger
and
Hiptmair, Ralf
2013.
Convergence of Lowest Order Semi-Lagrangian Schemes.
Foundations of Computational Mathematics,
Vol. 13,
Issue. 2,
p.
187.
Gong, Shihua
Lee, Young-Ju
Li, Yukun
and
Yu, Yue
2025.
Positivity and Maximum Principle Preserving Discontinuous Galerkin Finite Element Schemes for a Coupled Flow and Transport.
Journal of Scientific Computing,
Vol. 103,
Issue. 1,
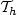 . For this method, we exhibit a “natural” norm || ||h,k for which we show that the discrete variational problem $P_h^k$
. For this method, we exhibit a “natural” norm || ||h,k for which we show that the discrete variational problem $P_h^k$ 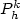 is well posed and weobtain an error estimate. We show that when k goes to zero problem $(P_h^k)$
is well posed and weobtain an error estimate. We show that when k goes to zero problem $(P_h^k)$ 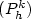 (resp. the || ||h,k norm)has as a limit problem (P h ) (resp. the || ||h norm) associated to the Galerkin discontinuousmethod. This extends to two and three space dimension our previous results obtained in one space dimension.
(resp. the || ||h,k norm)has as a limit problem (P h ) (resp. the || ||h norm) associated to the Galerkin discontinuousmethod. This extends to two and three space dimension our previous results obtained in one space dimension.