Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:48:41.095Z Has data issue: false hasContentIssue false
  • English
  • Français

hp-FEM for three-dimensional elastic plates

Published online by Cambridge University Press:  15 September 2002

Monique Dauge  and
Christoph Schwab
Monique Dauge
Affiliation:
Institut Mathématique, UMR 6625 du CNRS, Université de Rennes 1, Campus de Beaulieu, 35042 Rennes, France. [email protected].
Christoph Schwab
Affiliation:
Seminar für Angewandte Mathematik, ETH Zürich, ETHZ HG G58.1, CH 8092 Zürich, Switzerland.
Get access

Abstract

In this work, we analyze hierarchic hp-finite element discretizations of the full, three-dimensional plate problem. Based on two-scale asymptotic expansion of the three-dimensional solution, we give specific mesh design principles for the hp-FEM which allow to resolve the three-dimensional boundary layer profiles at robust, exponential rate.We prove that, as the plate half-thickness ε tends to zero, the hp-discretization is consistent with the three-dimensional solution to any power of ε in the energy norm for the degree $p={\cal O}(\left|{\log \varepsilon}\right|)$ 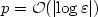and with ${\cal O}({p^4})$ 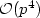degrees of freedom.

Keywords

Plateshp-finite elementsexponential convergenceasymptotic expansion.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 36 , Issue 4 , July 2002 , pp. 597 - 630
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Babuska, I. and Hierarchic, L. Li modelling of plates. Comput. & Structures 40 (1991) 419-430. CrossRef
Babuska, I. and The, L. Li problem of plate modelling - theoretical and computational results. Comput. Methods Appl. Mech. Engrg. 100 (1992) 249-273. CrossRef
Bolley, P., Camus, J. and Dauge, M., Régularité Gevrey pour le problème de Dirichlet dans des domaines à singularités coniques. Comm. Partial Differential Equations 10 (1985) 391-432. CrossRef
P.G. Ciarlet, Mathematical Elasticity II: Theory of Plates. Elsevier Publ., Amsterdam (1997).
Dauge, M., Djurdjevic, I., Faou, E. and Rössle, A., Eigenmodes asymptotic in thin elastic plates. J. Math. Pures Appl. 78 (1999) 925-964. CrossRef
Dauge, M. and Gruais, I., Asymptotics of arbitrary order for a thin elastic clamped plate. I: Optimal error estimates. Asymptot. Anal. 13 (1996) 167-197.
Dauge, M. and Gruais, I., Asymptotics of arbitrary order for a thin elastic clamped plate. II: Analysis of the boundary layer terms. Asymptot. Anal. 16 (1998) 99-124.
Dauge, M. and Gruais, I., Edge layers in thin elastic plates. Comput. Methods Appl. Mech. Engrg. 157 (1998) 335-347. CrossRef
M. Dauge, I. Gruais and A. Rössle, The influence of lateral boundary conditions on the asymptotics in thin elastic plates. SIAM J. Math. Anal. 31 (1999/00) 305-345 (electronic).
E. Faou, Développements asymptotiques dans les coques linéairement élastiques. Thèse, Université de Rennes 1 (2000).
Faou, E., Élasticité linéarisée tridimensionnelle pour une coque mince : résolution en série formelle en puissances de l'épaisseur. C. R. Acad. Sci. Paris Sér. I Math. 330 (2000) 415-420. CrossRef
Gregory, R.D. and Wan, F.Y., Decaying states of plane strain in a semi-infinite strip and boundary conditions for plate theory. J. Elasticity 14 (1984) 27-64. CrossRef
Guo, B. and Babuska, I., Regularity of the solutions for elliptic problems on nonsmooth domains in R 3. I. Countably normed spaces on polyhedral domains. Proc. Roy. Soc. Edinburgh Sect. A 127 (1997) 77-126. CrossRef
B. Guo and I. Babuska, Regularity of the solutions for elliptic problems on nonsmooth domains in R 3. II. Regularity in neighbourhoods of edges. Proc. Roy. Soc. Edinburgh Sect. A 127 (1997).
Kondrat'ev, V.A., Boundary-value problems for elliptic equations in domains with conical or angular points. Trans. Moscow Math. Soc. 16 (1967) 227-313.
Melenk, J.M. and Schwab, C., H P FEM for reaction-diffusion equations. I. Robust exponential convergence. SIAM J. Numer. Anal. 35 (1998) 1520-1557 (electronic). CrossRef
Morrey, C.B. and Nirenberg, L., On the analyticity of the solutions of linear elliptic systems of partial differential equations. Comm. Pure Appl. Math. 10 (1957) 271-290. CrossRef
Schwab, C., Boundary layer resolution in hierarchical models of laminated composites. RAIRO Modél. Math. Anal. Numér. 28 (1994) 517-537. CrossRef
C. Schwab,p - and hp -finite element methods. Theory and applications in solid and fluid mechanics. The Clarendon Press Oxford University Press, New York (1998).
Schwab, C. and Wright, S., Boundary layer approximation in hierarchical beam and plate models. J. Elasticity 38 (1995) 1-40. CrossRef
Stein, E. and Ohnimus, S., Coupled model- and solution-adaptivity in the finite-element method. Comput. Methods Appl. Mech. Engrg. 150 (1997) 327-350. Symposium on Advances in Computational Mechanics, Vol. 2 (Austin, TX, 1997). CrossRef