Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bianco, Franca
Puppo, Gabriella
and
Russo, Giovanni
1999.
High-Order Central Schemes for Hyperbolic Systems of Conservation Laws.
SIAM Journal on Scientific Computing,
Vol. 21,
Issue. 1,
p.
294.
Dhia, Anne-Sophie Bonnet-Ben
Hazard, Christophe
and
Lohrengel, Stephanie
1999.
A Singular Field Method for the Solution of Maxwell's Equations in Polyhedral Domains.
SIAM Journal on Applied Mathematics,
Vol. 59,
Issue. 6,
p.
2028.
Bal, Guillaume
1999.
First-Order Corrector for the Homogenization of the Criticality Eigenvalue Problem in the Even Parity Formulation of the Neutron Transport.
SIAM Journal on Mathematical Analysis,
Vol. 30,
Issue. 6,
p.
1208.
Sangalli, Giancarlo
2000.
Global and Local Error Analysis for the Residual-Free Bubbles Method Applied to Advection-Dominated Problems.
SIAM Journal on Numerical Analysis,
Vol. 38,
Issue. 5,
p.
1496.
Levy, Doron
Puppo, Gabriella
and
Russo, Giovanni
2000.
Compact Central WENO Schemes for Multidimensional Conservation Laws.
SIAM Journal on Scientific Computing,
Vol. 22,
Issue. 2,
p.
656.
Gallouët, Thierry
Herbin, Raphaèle
and
Vignal, Marie Hélène
2000.
Error Estimates on the Approximate Finite Volume Solution of Convection Diffusion Equations with General Boundary Conditions.
SIAM Journal on Numerical Analysis,
Vol. 37,
Issue. 6,
p.
1935.
Kurganov, Alexander
and
Levy, Doron
2000.
A Third-Order Semidiscrete Central Scheme for Conservation Laws and Convection-Diffusion Equations.
SIAM Journal on Scientific Computing,
Vol. 22,
Issue. 4,
p.
1461.
Caorsi, Salvatore
Fernandes, Paolo
and
Raffetto, Mirco
2000.
On the Convergence of Galerkin Finite Element Approximations of Electromagnetic Eigenproblems.
SIAM Journal on Numerical Analysis,
Vol. 38,
Issue. 2,
p.
580.
Nicaise, Serge
2000.
Exact Boundary Controllability of Maxwell's Equations in Heterogeneous Media and an Application to an Inverse Source Problem.
SIAM Journal on Control and Optimization,
Vol. 38,
Issue. 4,
p.
1145.
Bal, Guillaume
and
Ryzhik, Leonid
2000.
Diffusion Approximation of Radiative Transfer Problems with Interfaces.
SIAM Journal on Applied Mathematics,
Vol. 60,
Issue. 6,
p.
1887.
Liotta, Salvatore Fabio
Romano, Vittorio
and
Russo, Giovanni
2000.
Central Schemes for Balance Laws of Relaxation Type.
SIAM Journal on Numerical Analysis,
Vol. 38,
Issue. 4,
p.
1337.
Nicaise, Serge
2001.
Edge Elements on Anisotropic Meshes and Approximation of the Maxwell Equations.
SIAM Journal on Numerical Analysis,
Vol. 39,
Issue. 3,
p.
784.
Sun, Din-Kow
Lee, Jin-Fa
and
Cendes, Zoltan
2001.
Construction of Nearly Orthogonal Nedelec Bases for Rapid Convergence with Multilevel Preconditioned Solvers.
SIAM Journal on Scientific Computing,
Vol. 23,
Issue. 4,
p.
1053.
Kurganov, Alexander
Noelle, Sebastian
and
Petrova, Guergana
2001.
Semidiscrete Central-Upwind Schemes for Hyperbolic Conservation Laws and Hamilton--Jacobi Equations.
SIAM Journal on Scientific Computing,
Vol. 23,
Issue. 3,
p.
707.
Hiptmair, R.
2002.
Symmetric Coupling for Eddy Current Problems.
SIAM Journal on Numerical Analysis,
Vol. 40,
Issue. 1,
p.
41.
Bal, Guillaume
2002.
Transport Through Diffusive and Nondiffusive Regions, Embedded Objects, and Clear Layers.
SIAM Journal on Applied Mathematics,
Vol. 62,
Issue. 5,
p.
1677.
Chambolle, A.
and
Bonnetier, E.
2002.
Computing the Equilibrium Configuration of Epitaxially Strained Crystalline Films.
SIAM Journal on Applied Mathematics,
Vol. 62,
Issue. 4,
p.
1093.
Levy, Doron
Puppo, Gabriella
and
Russo, Giovanni
2002.
A Fourth-Order Central WENO Scheme for Multidimensional Hyperbolic Systems of Conservation Laws.
SIAM Journal on Scientific Computing,
Vol. 24,
Issue. 2,
p.
480.
Guermond, J. L.
and
Shen, Jie
2003.
Velocity-Correction Projection Methods for Incompressible Flows.
SIAM Journal on Numerical Analysis,
Vol. 41,
Issue. 1,
p.
112.
Droniou, Jérôme
Gallouët, Thierry
and
Herbin, Raphaèle
2003.
A Finite Volume Scheme for a Noncoercive Elliptic Equation with Measure Data.
SIAM Journal on Numerical Analysis,
Vol. 41,
Issue. 6,
p.
1997.
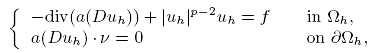
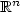 whose boundary ∂Ωh contains an oscillating part with respect to hwhen h tends to ∞. The oscillating boundary is defined by a set of cylinders with axis 0xn that are h -1-periodically distributed. We prove that the limit problem in the domain corresponding tothe oscillating boundary identifieswith a diffusion operator with respect tox n coupled with an algebraic problemfor the limit fluxes.
whose boundary ∂Ωh contains an oscillating part with respect to hwhen h tends to ∞. The oscillating boundary is defined by a set of cylinders with axis 0xn that are h -1-periodically distributed. We prove that the limit problem in the domain corresponding tothe oscillating boundary identifieswith a diffusion operator with respect tox n coupled with an algebraic problemfor the limit fluxes.

