Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T20:12:04.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite element approximation of finitely extensible nonlinearelastic dumbbell models for dilute polymers

Published online by Cambridge University Press:  13 February 2012

John W. Barrett  and
Endre Süli
John W. Barrett
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK. j.barrett@ imperial.ac.uk
Endre Süli
Affiliation:
Mathematical Institute, University of Oxford, 24–29 St. Giles’, OX1 3LB Oxford, UK; endre.suli@ maths.ox.ac.uk
Get access

Abstract

We construct a Galerkin finite element method for the numerical approximation of weaksolutions to a general class of coupled FENE-type finitely extensible nonlinear elasticdumbbell models that arise from the kinetic theory of dilute solutions of polymericliquids with noninteracting polymer chains. The class of models involves the unsteadyincompressible Navier–Stokes equations in a bounded domainΩ ⊂ ℝd, d = 2 or 3, forthe velocity and the pressure of the fluid, with an elastic extra-stress tensor appearingon the right-hand side in the momentum equation. The extra-stress tensor stems from therandom movement of the polymer chains and is defined through the associated probabilitydensity function that satisfies a Fokker–Planck type parabolic equation, a crucial featureof which is the presence of a centre-of-mass diffusion term. We require no structuralassumptions on the drag term in the Fokker–Planck equation; in particular, the drag termneed not be corotational. We perform a rigorous passage to the limit as first the spatialdiscretization parameter, and then the temporal discretization parameter tend to zero, andshow that a (sub)sequence of these finite element approximations converges to a weaksolution of this coupled Navier–Stokes–Fokker–Planck system. 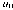The passage to the limit isperformed under minimal regularity assumptions on the data: a square-integrable anddivergence-free initial velocity datum \hbox{$\absundertilde$}u0~ for the Navier–Stokes equation and a nonnegative initial probabilitydensity function ψ0 for the Fokker–Planck equation, which hasfinite relative entropy with respect to the Maxwellian M.

Keywords

Finite element methodconvergence analysisexistence of weak solutionskinetic polymer modelsFENE dumbbellNavier–Stokes equationsFokker–Planck equations
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 46 , Issue 4 , July 2012 , pp. 949 - 978
Copyright
© EDP Sciences, SMAI, 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, L., Transport equation and Cauchy problem for BV vector fields. Invent. Math. 158 (2004) 227–260. Google Scholar
Barrett, J.W. and Nürnberg, R., Convergence of a finite-element approximation of surfactant spreading on a thin film in the presence of van der Waals forces. IMA J. Numer. Anal. 24 (2004) 323–363. Google Scholar
Barrett, J.W. and Süli, E., Existence of global weak solutions to some regularized kinetic models of dilute polymers. Multiscale Model. Simul. 6 (2007) 506–546. Google Scholar
Barrett, J.W. and Süli, E., Existence of global weak solutions to dumbbell models for dilute polymers with microscopic cut-off. Math. Models Methods Appl. Sci. 18 (2008) 935–971. Google Scholar
Barrett, J.W. and Süli, E., Numerical approximation of corotational dumbbell models for dilute polymers. IMA J. Numer. Anal. 29 (2009) 937–959. Google Scholar
J.W. Barrett and E. Süli, Existence and equilibration of global weak solutions to finitely extensible nonlinear bead-spring chain models for dilute polymers. Available as arXiv:1004.1432v2 [math.AP] from http://arxiv.org/abs/1004.1432 (2010).
Barrett, J.W. and Süli, E., Existence and equilibration of global weak solutions to kinetic models for dilute polymers I : Finitely extensible nonlinear bead-spring chains. Math. Models Methods Appl. Sci. 21 (2011) 1211–1289. Google Scholar
Barrett, J.W. and Süli, E., Finite element approximation of kinetic dilute polymer models with microscopic cut-off. ESAIM : M2AN 45 (2011) 39–89. Google Scholar
J.W. Barrett and E. Süli, Existence and equilibration of global weak solutions to kinetic models for dilute polymers II : Hookean bead-spring chains. Math. Models Methods Appl. Sci. 22 (2012), to appear. Extended version available as arXiv:1008.3052 [math.AP] from http://arxiv.org/abs/1008.3052.
Bhave, A.V., Armstrong, R.C. and Brown, R.A., Kinetic theory and rheology of dilute, nonhomogeneous polymer solutions. J. Chem. Phys. 95 (1991) 2988–3000. Google Scholar
J. Brandts, S. Korotov, M. Křížek and J. Šolc, On acute and nonobtuse simplicial partitions. Helsinki University of Technology, Institute of Mathematics, Research Reports, A503 (2006).
F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods. Springer-Verlag, Berlin (1991).
Ph. Ciarlet, The Finite Element Method for Elliptic Problems. North-Holland, Amsterdam (1978).
Degond, P. and Liu, H., Kinetic models for polymers with inertial effects. Netw. Heterog. Media 4 (2009) 625–647. Google Scholar
DiPerna, R.J. and Lions, P.-L., Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98 (1989) 511–547. Google Scholar
Eppstein, D., Sullivan, J.M. and Üngör, A., Tiling space and slabs with acute tetrahedra. Comput. Geom. 27 (2004) 237–255. Google Scholar
Grün, G. and Rumpf, M., Nonnegativity preserving numerical schemes for the thin film equation. Numer. Math. 87 (2000) 113–152. Google Scholar
Itoh, J.-I. and Zamfirescu, T., Acute triangulations of the regular dodecahedral surface. Eur. J. Comb. 28 (2007) 1072–1086. Google Scholar
Knezevic, D.J. and Süli, E., A deterministic multiscale approach for simulating dilute polymeric fluids, in BAIL 2008 – boundary and interior layers. Lect. Notes Comput. Sci. Eng. 69 (2009) 23–38. Google Scholar
Knezevic, D.J. and Süli, E., A heterogeneous alternating-direction method for a micro-macro dilute polymeric fluid model. ESAIM : M2AN 43 (2009) 1117–1156. Google Scholar
Knezevic, D.J. and Süli, E., Spectral Galerkin approximation of Fokker-Planck equations with unbounded drift. ESAIM : M2AN 43 (2009) 445–485. Google Scholar
Korotov, S. and Křížek, M., Acute type refinements of tetrahedral partitions of polyhedral domains. SIAM J. Numer. Anal. 39 (2001) 724–733. Google Scholar
Korotov, S. and Křížek, M., Global and local refinement techniques yielding nonobtuse tetrahedral partitions. Comput. Math. Appl. 50 (2005) 1105–1113. Google Scholar
Lions, P.-L. and Masmoudi, N., Global existence of weak solutions to some micro-macro models. C. R. Math. Acad. Sci. Paris 345 (2007) 15–20. Google Scholar
Masmoudi, N., Well posedness of the FENE dumbbell model of polymeric flows. Comm. Pure Appl. Math. 61 (2008) 1685–1714. Google Scholar
N. Masmoudi, Global existence of weak solutions to the FENE dumbbell model of polymeric flows. Preprint (2010).
R.H. Nochetto, Finite element methods for parabolic free boundary problems, in Advances in Numerical Analysis I. Lancaster (1990); Oxford Sci. Publ., Oxford Univ. Press, New York (1991) 34–95.
Schieber, J.D., Generalized Brownian configuration field for Fokker–Planck equations including center-of-mass diffusion. J. Non-Newtonian Fluid Mech. 135 (2006) 179–181. Google Scholar
W.H.A. Schilders and E.J.W. ter Maten, Eds., Numerical Methods in Electromagnetics, Handbook of Numerical Analysis XIII. North-Holland, Amsterdam (2005).
R. Temam, Navier–Stokes Equations. Theory and Numerical Analysis, Studies in Mathematics and its Applications 2. North-Holland, Amsterdam (1984).