Published online by Cambridge University Press: 15 August 2004
We consider a fully practical finite element approximation of the following degenerate system $$ {\frac{\partial }{\partial t}} \rho(u)- \nabla . ( \,\alpha(u) \,\nabla u ) \ni \sigma(u)\,|\nabla\phi|^2 ,\quad \nabla . (\, \sigma(u) \,\nabla \phi ) = 0$$ 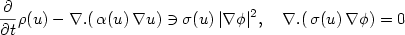 subject to an initial condition on the temperature, u,and boundary conditions on both u and the electric potential, ϕ. In the above p(u) is the enthalpy incorporating the latent heat of melting, α(u) > 0 is the temperature dependent heat conductivity, and σ(u) > 0is the electricalconductivity. The latter is zero in the frozen zone, u ≤ 0,which gives rise to the degeneracy in this Stefan system.In addition to showing stability bounds, we prove (subsequence) convergence of our finite element approximation intwo and three space dimensions. The latter is non-trivial due to the degeneracy in σ(u)and the quadratic nature of the Joule heating term forcing the Stefan problem.Finally, some numerical experiments are presented in two space dimensions.
subject to an initial condition on the temperature, u,and boundary conditions on both u and the electric potential, ϕ. In the above p(u) is the enthalpy incorporating the latent heat of melting, α(u) > 0 is the temperature dependent heat conductivity, and σ(u) > 0is the electricalconductivity. The latter is zero in the frozen zone, u ≤ 0,which gives rise to the degeneracy in this Stefan system.In addition to showing stability bounds, we prove (subsequence) convergence of our finite element approximation intwo and three space dimensions. The latter is non-trivial due to the degeneracy in σ(u)and the quadratic nature of the Joule heating term forcing the Stefan problem.Finally, some numerical experiments are presented in two space dimensions.