Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T18:10:29.842Z Has data issue: false hasContentIssue false
  • English
  • Français

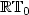Analysis of a new augmented mixed finite element methodfor linear elasticity allowing $\mathbb{RT}_0$ - $\mathbb{P}_1$ 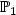- $\mathbb{P}_0$ 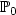approximations

Published online by Cambridge University Press:  23 February 2006

Gabriel N. Gatica
Gabriel N. Gatica*
Affiliation:
GI2MA, Departamento de Ingeniería Matemática, Universidad de Concepción, Casilla 160-C, Concepción, Chile. [email protected]
Get access

Abstract

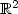We present a new stabilized mixed finite element method for the linear elasticity problem in $\mathbb{R}^2$ . Theapproach is based on the introduction of Galerkin least-squares terms arising from the constitutive andequilibrium equations, and from the relation defining the rotation in terms of the displacement. We show thatthe resulting augmented variational formulation and the associated Galerkin scheme are well posed, and thatthe latter becomes locking-free and asymptotically locking-free for Dirichlet and mixed boundary conditions,respectively. In particular, the discrete scheme allows the utilization of Raviart–Thomas spaces of lowestorder for the stress tensor, piecewise linear elements for the displacement, and piecewise constants for therotation. In the case of mixed boundary conditions, the essential one (Neumann) is imposed weakly, whichyields the introduction of the trace of the displacement as a suitable Lagrange multiplier. This trace isthen approximated by piecewise linear elements on an independent partition of the Neumann boundary whose meshsize needs to satisfy a compatibility condition with the mesh size associated to the triangulation of thedomain. Several numerical results illustrating the good performance of the augmented mixed finite elementscheme in the case of Dirichlet boundary conditions are also reported.

Keywords

Mixed-FEMaugmented formulationlinear elasticitylocking-free.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 40 , Issue 1 , January 2006 , pp. 1 - 28
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnold, D.N., Brezzi, F. and Douglas, J., PEERS: A new mixed finite element method for plane elasticity. Japan J. Appl. Math. 1 (1984) 347–367. CrossRef
Arnold, D.N., Brezzi, F. and Fortin, M., A stable finite element method for the Stokes equations. Calcolo 21 (1984) 337–344. CrossRef
Arnold, D.N., Douglas, J. and Gupta, Ch.P., A family of higher order mixed finite element methods for plane elasticity. Numer. Math. 45 (1984) 1–22. CrossRef
Arnold, D. and Falk, R., Well-posedness of the fundamental boundary value problems for constrained anisotropic elastic materials. Arch. Rational Mech. Analysis 98 (1987) 143–190. CrossRef
Babuška, I. and Gatica, G.N., On the mixed finite element method with Lagrange multipliers. Numer. Methods Partial Differential Equations 19 (2003) 192–210. CrossRef
Barrientos, M., Gatica, G.N. and Stephan, E.P., A mixed finite element method for nonlinear elasticity: two-fold saddle point approach and a posteriori error estimate. Numer. Math. 91 (2002) 197–222. CrossRef
T.P. Barrios, G.N. Gatica and F. Paiva, A wavelet-based stabilization of the mixed finite element method with Lagrange multipliers. Appl. Math. Lett. (in press).
D. Braess, Finite Elements. Theory, Fast Solvers, and Applications in Solid Mechanics. Cambridge University Press (1997).
Brezzi, F. and Douglas, J., Stabilized mixed methods for the Stokes problem. Numer. Math. 53 (1988) 225–235. CrossRef
F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods. Springer-Verlag (1991).
Brezzi, F. and Fortin, M., A minimal stabilisation procedure for mixed finite element methods. Numer. Math. 89 (2001) 457–491. CrossRef
Brezzi, F., Douglas, J. and Marini, L.D., Variable degree mixed methods for second order elliptic problems. Mat. Apl. Comput. 4 (1985) 19–34.
Brezzi, F., Douglas, J. and Marini, L.D., Two families of mixed finite elements for second order elliptic problems. Numer. Math. 47 (1985) 217–235. CrossRef
Brezzi, F., Fortin, M. and Marini, L.D., Mixed finite element methods with continuous stresses. Math. Models Methods Appl. Sci. 3 (1993) 275–287. CrossRef
D. Chapelle and R. Stenberg, Locking-free mixed stabilized finite element methods for bending-dominated shells, in Plates and shells (Quebec, QC, 1996), American Mathematical Society, Providence, RI, CRM Proceedings Lecture Notes 21 (1999) 81–94.
P.G. Ciarlet, The Finite Element Method for Elliptic Problems. North-Holland (1978).
Douglas, J. and Wan, J., An absolutely stabilized finite element method for the Stokes problem. Math. Comput. 52 (1989) 495–508. CrossRef
Duan, H.-Y. and Liang, G.-P., Analysis of some stabilized low-order mixed finite element methods for Reissner-Mindlin plates. Comput. Methods Appl. Mech. Engrg. 191 (2001) 157–179.
L.P. Franca, New Mixed Finite Element Methods. Ph.D. Thesis, Stanford University (1987).
L.P. Franca and T.J.R. Hughes, Two classes of finite element methods. Comput. Methods Appl. Mech. Engrg. 69 (1988) 89–129.
Franca, L.P. and Russo, A., Unlocking with residual-free bubbles. Comput. Methods Appl. Mech. Engrg. 142 (1997) 361–364. CrossRef
Franca, L.P. and Stenberg, R., Error analysis of Galerkin least squares methods for the elasticity equations. SIAM J. Numer. Anal. 28 (1991) 1680–1697. CrossRef
Horgan, C.O., Korn's inequalities and their applications in continuum mechanics. SIAM Rev. 37 (1995) 491–511. CrossRef
Horgan, C.O. and Knowles, J.K., Eigenvalue problems associated with Korn's inequalities. Arch. Rational Mech. Anal. 40 (1971) 384–402. CrossRef
Horgan, C.O. and Payne, L.E., On inequalities of Korn, Friedrichs and Babuška-Aziz. Arch. Rational Mech. Analysis 82 (1983) 165–179. CrossRef
Kechkar, N. and Silvester, D., Analysis of locally stabilized mixed finite element methods for the Stokes problem. Math. Comput. 58 (1992) 1–10. CrossRef
Lube, G. and Auge, A., Stabilized mixed finite element approximations of incompressible flow problems. Zeitschrift für Angewandte Mathematik und Mechanik 72 (1992) T483–T486. CrossRef
W. McLean, Strongly Elliptic Systems and Boundary Integral Equations. Cambridge University Press (2000).
Masud, A. and Hughes, T.J.R., A stabilized mixed finite element method for Darcy flow. Comput. Methods Appl. Mech. Engrg. 191 (2002) 4341–4370. CrossRef
Nascimbene, R. and Venini, P., A new locking-free equilibrium mixed element for plane elasticity with continuous displacement interpolation. Comput. Methods Appl. Mech. Engrg 191 (2002) 1843–1860. CrossRef
Norburn, S. and Silvester, D., Fourier analysis of stabilized $Q\sb 1$ - $Q\sb 1$ mixed finite element approximation. SIAM J. Numer. Anal. 39 (2001) 817–833. CrossRef
Stenberg, R., A family of mixed finite elements for the elasticity problem. Numer. Math. 53 (1988) 513–538. CrossRef
Zhou, T., Stabilized hybrid finite element methods based on the combination of saddle point principles of elasticity problems. Math. Comput. 72 (2003) 1655–1673. CrossRef
Zhou, T. and Zhou, L., Analysis of locally stabilized mixed finite element methods for the linear elasticity problem. Chinese J. Engrg Math. 12 (1995) 1–6.