Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T15:39:29.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted regularization for composite materialsin electromagnetism

Published online by Cambridge University Press:  03 November 2009

Patrick Ciarlet Jr. ,
François Lefèvre ,
Stéphanie Lohrengel  and
Serge Nicaise
Patrick Ciarlet Jr.
Affiliation:
Laboratoire POEMS, UMR 7231 CNRS/ENSTA/INRIA, ENSTA ParisTech, 32 boulevard Victor, 75739 Paris Cedex 15, France. [email protected]
François Lefèvre
Affiliation:
Laboratoire de Mathématiques, FRE 3111, UFR Sciences exactes et naturelles, Université de Reims Champagne-Ardenne, Moulin de la Housse – B.P. 1039, 51687 Reims Cedex 2, France. [email protected]; [email protected]
Stéphanie Lohrengel
Affiliation:
Laboratoire de Mathématiques, FRE 3111, UFR Sciences exactes et naturelles, Université de Reims Champagne-Ardenne, Moulin de la Housse – B.P. 1039, 51687 Reims Cedex 2, France. [email protected]; [email protected]
Serge Nicaise
Affiliation:
LAMAV, Université de Valenciennes et du Hainaut Cambrésis, Le Mont Houy, 59313 Valenciennes Cedex 9, France. [email protected]
Get access

Abstract

In this paper, a weighted regularization method for the time-harmonic Maxwell equationswith perfect conducting or impedance boundary condition in composite materials is presented.The computational domain Ω is the unionof polygonal or polyhedral subdomains made of different materials. As a result, the electromagnetic field presents singularitiesnear geometric singularities, which are the interior and exterior edges and corners. 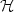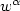The variational formulation of theweighted regularized problem is given on the subspace of ${\cal H}$ ( ${\bf curl}$ ;Ω)whose fields $\textit{\textbf{ u}}$ satisfy $w^\alpha$ div ( $\varepsilon{\textit{\textbf{u}}}$ 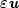)∈L2 (Ω) and have vanishing tangential traceor tangential trace in L2 ( $\partial\Omega$ 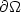). The weight function $w(\bf x)$ 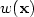is equivalentto the distance of $\bf x$ to the geometric singularities and the minimal weight parameter αis given in terms of the singular exponents of a scalar transmission problem.A density result is proven that guarantees the approximability of the solution field by piecewise regular fields.Numerical results for the discretization of the source problemby means of Lagrange Finite Elements of type P 1 and P 2 are given onuniform and appropriately refined two-dimensional meshes.The performance of the method in the case of eigenvalue problems is addressed.

Keywords

Maxwell's equationsinterface problemsingularities of solutionsdensity resultsweighted regularization
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 44 , Issue 1 , January 2010 , pp. 75 - 108
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amrouche, C., Bernardi, C., Dauge, M. and Girault, V., Vector potentials in three-dimensional non-smooth domains. Math. Meth. Appl. Sci. 21 (1998) 823–864. 3.0.CO;2-B>CrossRef
Assous, F., Degond, P., Heintzé, E., Raviart, P.-A. and Segré, J., On a finite element method for solving the three-dimensional Maxwell equations. J. Comput. Phys. 109 (1993) 222–237. CrossRef
Assous, F., Degond, P. and Segré, J., Numerical approximation of the Maxwell equations in inhomogeneous media by a P1 conforming finite element method. J. Comput. Phys. 128 (1996) 363–380. CrossRef
Assous, F., Ciarlet Jr, P.. and E. Sonnendrücker, Resolution of the Maxwell equations in a domain with reentrant corners. Math. Mod. Num. Anal. 32 (1998) 359–389. CrossRef
Assous, F., Ciarlet Jr, P.., P.-A. Raviart and E. Sonnendrücker, A characterization of the singular part of the solution to Maxwell's equations in a polyhedral domain. Math. Meth. Appl. Sci. 22 (1999) 485–499. 3.0.CO;2-E>CrossRef
Assous, F., Ciarlet Jr, P.. and J. Segré, Numerical solution to the time-dependent Maxwell equations in two-dimensional singular domains: the singular complement method. J. Comput. Phys. 161 (2000) 218–249. CrossRef
Birman, M. and Solomyak, M., L2 -theory of the Maxwell operator in arbitrary domains. Russ. Math. Surv. 42 (1987) 75–96. CrossRef
Birman, M. and Solomyak, M., On the main singularities of the electric component of the electro-magnetic field in regions with screens. St. Petersbg. Math. J. 5 (1993) 125–139.
Boffi, D., Brezzi, F. and Gastaldi, L., On the convergence of eigenvalues for mixed formulations. Annali Sc. Norm. Sup. Pisa Cl. Sci. 25 (1997) 131–154.
Bonnet-Ben Dhia, A.-S., Hazard, C. and Lohrengel, S., A singular field method for the solution of Maxwell's equations in polyhedral domains. SIAM J. Appl. Math. 59 (1999) 2028–2044.
Buffa, A., Ciarlet Jr, P.. and E. Jamelot, Solving electromagnetic eigenvalue problems in polyhedral domains. Numer. Math. 113 (2009) 497–518. CrossRef
Ciarlet Jr, P.., Augmented formulations for solving Maxwell equations. Comp. Meth. Appl. Mech. Eng. 194 (2005) 559–586.
Ciarlet Jr, P.. and G. Hechme, Computing electromagnetic eigenmodes with continuous Galerkin approximations. Comp. Meth. Appl. Mech. Eng. 198 (2008) 358–365.
P. Ciarlet Jr. and G. Hechme, Mixed, augmented variational formulations for Maxwell's equations: Numerical analysis via the macroelement technique. Numer. Math. (Submitted).
P. Ciarlet Jr., C. Hazard and S. Lohrengel, Les équations de Maxwell dans un polyèdre : un résultat de densité. C. R. Acad. Sci. Paris, Ser. I 326 (1998) 1305–1310.
M. Costabel and M. Dauge, Un résultat de densité pour les équations de Maxwell régularisées dans un domaine lipschitzien. C. R. Acad. Sci. Paris, Ser. I 327 (1998) 849–854.
Costabel, M. and Dauge, M., Singularities of electromagnetic fields in polyhedral domains. Arch. Rational Mech. Anal. 151 (2000) 221–276. CrossRef
Costabel, M. and Dauge, M., Weighted regularization of Maxwell's equations in polyhedral domains. Numer. Math. 93 (2002) 239–277. CrossRef
Costabel, M., Dauge, M. and Nicaise, S., Singularities of Maxwell interface problems. ESAIM: M2AN 33 (1999) 627–649. CrossRef
M. Dauge, Benchmark computations for Maxwell equations for the approximation of highly singular solutions. (2004). See Monique Dauge's personal web page at the location http://perso.univ-rennes1.fr/monique.dauge/core/index.html
Fernandes, P. and Gilardi, G., Magnetostatic and electrostatic problems in inhomogeneous anisotropic media with irregular boundary and mixed boundary conditions. Math. Models Meth. Appl. Sci. 7 (1997) 957–991. CrossRef
Grisvard, P., Edge behaviour of the solution of an elliptic problem. Math. Nachr. 132 (1987) 281–299. CrossRef
P. Grisvard, Singularities in boundary value problems, RMA 22. Masson (1992).
Hazard, C. and Lenoir, M., On the solution of time-harmonic scattering problems for Maxwell's equations. SIAM J. Math. Anal. 27 (1996) 1597–1630. CrossRef
Hazard, C. and Lohrengel, S., A singular field method for Maxwell's equations: numerical aspects for 2D magnetostatics. SIAM J. Numer. Anal. 40 (2002) 1021–1040. CrossRef
Heinrich, B., Nicaise, S. and Weber, B., Elliptic interface problems in axisymmetric domains. I: Singular functions of non-tensorial type. Math. Nachr. 186 (1997) 147–165. CrossRef
D. Leguillon and E. Sanchez-Palencia, Computation of singular solutions in elliptic problems and elasticity, RMA 5. Masson (1987).
Lohrengel, S. and Nicaise, S., Singularities and density problems for composite materials in electromagnetism. Comm. Partial Diff. Eq. 27 (2002) 1575–1623. CrossRef
Lubuma, J.M.-S. and Nicaise, S., Dirichlet problems in polyhedral domains. I: Regularity of the solutions. Math. Nachr. 168 (1994) 243–261. CrossRef
P. Monk, Finite element methods for Maxwell's equations. Oxford University Press, UK (2003).
M. Moussaoui, $H({\rm div},{\rm rot},\Omega)$ dans un polygone plan. C. R. Acad. Sci. Paris, Ser. I 322 (1996) 225–229.
S. Nazarov and B. Plamenevsky, Elliptic problems in domains with piecewise smooth boundaries, Exposition in Mathematics 13. De Gruyter, Berlin, Germany (1994).
S. Nicaise, Polygonal interface problems. Peter Lang, Berlin, Germany (1993).
Nicaise, S. and Sändig, A.-M., General interface problems I, II. Math. Meth. Appl. Sci. 17 (1994) 395–450. CrossRef
B. Smith, P. Bjorstad and W. Gropp, Domain decomposition. Parallel multilevel methods for elliptic partial differential equations. Cambridge University Press, New York, USA (1996).