Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T01:25:49.856Z Has data issue: false hasContentIssue false
  • English
  • Français

On the two-dimensional compressible isentropic Navier–Stokes equations

Published online by Cambridge University Press:  15 January 2003

Catherine Giacomoni  and
Pierre Orenga
Catherine Giacomoni
Affiliation:
Systèmes Physiques de l'Environnement, UMR CNRS 6134, Université de Corse, Quartier Grossetti, BP 52, 20250 Corte, France. [email protected]., [email protected].
Pierre Orenga
Affiliation:
Systèmes Physiques de l'Environnement, UMR CNRS 6134, Université de Corse, Quartier Grossetti, BP 52, 20250 Corte, France. [email protected]., [email protected].
Get access

Abstract

We analyze the compressible isentropic Navier–Stokes equations (Lions, 1998) in the two-dimensional case with $\gamma=\displaystyle{{c_{p}}/{c_{v}}}=2$ 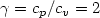. These equations also modelizethe shallow water problem in height-flow rate formulation used tosolve the flow in lakes and perfectly well-mixed sea. We establisha convergence result for the time-discretized problem when themomentum equation and the continuity equation are solved with theGalerkin method, without adding a penalization term in thecontinuity equation as it is made in Lions (1998). The secondpart is devoted to the numerical analysis and mainly deals withproblems of geophysical fluids. We compare the simulationsobtained with this compressible isentropic Navier–Stokes model andthose obtained with a shallow water model (Di Martino et al., 1999). At first,the computations are executed on a simplified domain in order tovalidate the method by comparison with existing numerical resultsand then on a real domain: the dam of Calacuccia (France). At last, we numerically implement an analyticalexample presented by Weigant (1995) which shows thateven if the data are rather smooth, we cannot have bounds onρ in Lp for p large if $\gamma<2$ 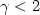when N=2.

Keywords

Navier–Stokescompressibleshallow watertime-discretisationGalerkin.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 36 , Issue 6 , November 2002 , pp. 1091 - 1109
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coifman, R., Lions, P.L., Meyer, Y. and Semmes, S., Compensated-compactness and Hardy spaces. J. Math. Pures Appl. 72 (1993) 247-286.
DiPerna, R.J. and Lions, P.L., On the cauchy problem for boltzman equations: global existence and weak stability. C.R. Acad. Sci. Paris Sér. I Math. 306 (1988) 343-346.
DiPerna, R.J. and Lions, P.L., Ordinary differential equations, transport theory and sobolev spaces. Invent. Math. 98 (1989) 511-547. CrossRef
V. Girault and P.A. Raviart, Finite Elements Methods of the Navier-Stokes Equations. Springer-Verlag (1986).
P.L. Lions, Mathematical Topics in Fluid Mechanics, Incompressible models. Vol. 1, Oxford Science Publications (1996).
P.L. Lions, Mathematical Topics in Fluid Mechanics, Compressible models. Vol. 2, Oxford Science Publications (1998).
Di Martino, B., Chatelon, F.J. and Orenga, P., The nonlinear Galerkin's method applied to the shallow water equations. Math. Models Methods Appl. Sci. 9 (1999) 825-854. CrossRef
P. Orenga, Analyse de quelques problèmes d'océanographie physique. Ph.D. thesis, Université de Corse, Corte (1992).
P. Orenga, Construction d'une base spéciale pour la résolution de quelques problèmes non linéaires d'océanographie physique en dimension deux, in Nonlinear partial differential equations and their applications, D. Cioranescu and J.L. Lions, Vol. 13. Longman, Pitman Res. Notes Math. Ser. 391 (1998) 234-258.
V.A. Solonnikov, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 56 (1976) 128-142. English translation in J. Soviet Math. 14 (1980) 1120-1133.
Weigant, V.A., An exemple of non-existence globally in time of a solution of the Navier-Stokes equations for a compressible viscous barotropic fluid. Russian Acad. Sci. Doklady Mathematics 50 (1995) 397-399.
E. Zeidler, Fixed-point theorems, in Nonlinear Functional Analysis and its Applications, Vol. 1, Springer-Verlag (1986).