Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T08:16:37.472Z Has data issue: false hasContentIssue false
  • English
  • Français

On the motion of a body in thermal equilibriumimmersedin a perfect gas

Published online by Cambridge University Press:  27 March 2008

Kazuo Aoki ,
Guido Cavallaro ,
Carlo Marchioro  and
Mario Pulvirenti
Kazuo Aoki
Affiliation:
Department of Mechanical Engineering and Science and Advanced Research Institute of Fluid Science and Engineering, Graduate School of Engineering, Kyoto University, Kyoto 606-8501, Japan. [email protected]
Guido Cavallaro
Affiliation:
Dipartimento di Matematica, Università di Roma “La Sapienza", Piazzale A. Moro 2, 00185, Roma, Italy. [email protected]; [email protected]; [email protected]
Carlo Marchioro
Affiliation:
Dipartimento di Matematica, Università di Roma “La Sapienza", Piazzale A. Moro 2, 00185, Roma, Italy. [email protected]; [email protected]; [email protected]
Mario Pulvirenti
Affiliation:
Dipartimento di Matematica, Università di Roma “La Sapienza", Piazzale A. Moro 2, 00185, Roma, Italy. [email protected]; [email protected]; [email protected]
Get access

Abstract

We consider a body immersed in a perfect gas and moving under the action of a constant force.Body and gas are in thermal equilibrium. We assume a stochastic interaction body/medium: when a particle of the medium hits the body, it is absorbed and immediately re-emitted with a Maxwellian distribution. This system gives rise to a microscopic model of friction. 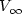We study the approach of the body velocity V(t) to the limiting velocity $V_\infty$ and prove that, under suitable smallness assumptions, the approach to equilibrium is $$|V(t)-V_\infty|\approx \frac{C}{t^{d+1}},$$ 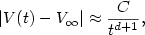where d is the dimension of the space, and C is a positive constant. This approach is not exponential, as typical in friction problems, and even slower than for the same problem with elastic collisions.

Keywords

Kinetic theory of gasesBoltzmann equationfree molecular gasfriction problemapproach to equilibrium.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 42 , Issue 2 , March 2008 , pp. 263 - 275
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braun, W. and Hepp, K., The Vlasov dynamics and its fluctuations in the $1/N$ limit of interacting classical particles. Comm. Math. Phys. 56 (1977) 101–113. CrossRef
Buttà, P., Caglioti, E. and Marchioro, C., On the long time behavior of infinitely extended systems of particles interacting via Kac Potentials. J. Stat. Phys. 108 (2002) 317–339. CrossRef
Caprino, S., Marchioro, C. and Pulvirenti, M., Approach to equilibrium in a microscopic model of friction. Comm. Math. Phys. 264 (2006) 167–189. CrossRef
Caprino, S., Cavallaro, G. and Marchioro, C., On a microscopic model of viscous friction. Math. Models Methods Appl. Sci. 17 (2007) 1369–1403. CrossRef
Cavallaro, G., On the motion of a convex body interacting with a perfect gas in the mean-field approximation. Rend. Mat. Appl. 27 (2007) 123–145.
Dobrushin, R.L., Vlasov equations. Sov. J. Funct. Anal. 13 (1979) 115–123. CrossRef
Gruber, C. and Piasecki, J., Stationary motion of the adiabatic piston. Physica A 268 (1999) 412–423. CrossRef
J.L. Lebowitz, J. Piasecki and Y. Sinai, Scaling dynamics of a massive piston in a ideal gas, in Hard Ball Systems and the Lorentz Gas, Encycl. Math. Sci. 101, Springer, Berlin (2000) 217–227.
H. Neunzert, An Introduction to the Nonlinear Boltzmann-Vlasov Equation, in Kinetic Theories and the Boltzmann Equation, Montecatini (1981), Lecture Notes in Math. 1048, Springer, Berlin (1984) 60–110.
Spohn, H., On the Vlasov hierarchy. Math. Meth. Appl. Sci. 3 (1981) 445–455. CrossRef