No CrossRef data available.
Article contents
Non-Trapping sets and Huygens Principle
Published online by Cambridge University Press: 15 August 2002
Abstract
We consider the evolution of a set $\Lambda\subset \mathbb R^2$ 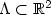 according to theHuygens principle: i.e. the domain at time t>0, Λt, is the set ofthe points whose distance from Λ is lower thant. We give some general results for this evolution,with particular care given to the behavior of the perimeter of theevoluted set as a function of time. We define a class of sets (non-trapping sets) for which the perimeter is a continuous function of t, andwe give an algorithm to approximate the evolution.Finally we restrict our attention to the class of sets for which the turning angle of the boundary is greater than -π (see [2]).For this class of sets we prove that the perimeter is a Lipschitz-continuous function of t. This evolution problem is relevant for the applicationsbecause it is used as a model for solid fuel combustion.
according to theHuygens principle: i.e. the domain at time t>0, Λt, is the set ofthe points whose distance from Λ is lower thant. We give some general results for this evolution,with particular care given to the behavior of the perimeter of theevoluted set as a function of time. We define a class of sets (non-trapping sets) for which the perimeter is a continuous function of t, andwe give an algorithm to approximate the evolution.Finally we restrict our attention to the class of sets for which the turning angle of the boundary is greater than -π (see [2]).For this class of sets we prove that the perimeter is a Lipschitz-continuous function of t. This evolution problem is relevant for the applicationsbecause it is used as a model for solid fuel combustion.
Keywords
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 33 , Issue 3 , May 1999 , pp. 517 - 530
- Copyright
- © EDP Sciences, SMAI, 1999


