Published online by Cambridge University Press: 15 August 2002
Let Φ : H → R be a C 2 function on a real Hilbert space and ∑ ⊂ H x R the manifold defined by ∑ := Graph (Φ). We study the motion of a material point with unit mass, subjected to stay on Σ and which moves under the action of the gravity force(characterized by g>0), the reaction force and the friction force ( $\gamma>0$ 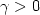 is the friction parameter). For any initial conditions at time t=0, we prove the existence of a trajectory x(.) defined on R +. We are then interested in the asymptotic behaviour of the trajectories when t → +∞. More precisely, we prove the weak convergence of the trajectories when Φ is convex. When Φ admits a strong minimum, we show moreover that the mechanical energy exponentially decreases to its minimum.
is the friction parameter). For any initial conditions at time t=0, we prove the existence of a trajectory x(.) defined on R +. We are then interested in the asymptotic behaviour of the trajectories when t → +∞. More precisely, we prove the weak convergence of the trajectories when Φ is convex. When Φ admits a strong minimum, we show moreover that the mechanical energy exponentially decreases to its minimum.