Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eymard, Robert
Gallouët, Thierry
and
Herbin, Raphaèle
2000.
Solution of Equation in ℝn (Part 3), Techniques of Scientific Computing (Part 3).
Vol. 7,
Issue. ,
p.
713.
Karlsen, Kenneth Hvistendahl
and
Risebro, Nils Henrik
2001.
Convergence of finite difference schemes for viscous and inviscid conservation laws with rough coefficients.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 35,
Issue. 2,
p.
239.
Kröner, D.
and
Gessner, T.
2001.
Godunov Methods.
p.
527.
Levi, Laurent
2001.
Obstacle problems for scalar conservation laws.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 35,
Issue. 3,
p.
575.
Ohlberger, Mario
2001.
A posteriorierror estimates for vertex centered finite volume approximations of convection-diffusion-reaction equations.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 35,
Issue. 2,
p.
355.
Küther, Marc
2001.
Error Estimates for the Staggered Lax--Friedrichs Scheme on Unstructured Grids.
SIAM Journal on Numerical Analysis,
Vol. 39,
Issue. 4,
p.
1269.
Klöfkorn, Robert
Kröner, Dietmar
and
Ohlberger, Mario
2002.
Local adaptive methods for convection dominated problems.
International Journal for Numerical Methods in Fluids,
Vol. 40,
Issue. 1-2,
p.
79.
Noelle, Sebastian
and
Westdickenberg, Michael
2003.
Geometric Analysis and Nonlinear Partial Differential Equations.
p.
417.
Junk, Michael
2003.
Meshfree Methods for Partial Differential Equations.
Vol. 26,
Issue. ,
p.
223.
Michel, Anthony
2003.
A Finite Volume Scheme for Two-Phase Immiscible Flow in Porous Media.
SIAM Journal on Numerical Analysis,
Vol. 41,
Issue. 4,
p.
1301.
Michel, Anthony
and
Vovelle, Julien
2003.
Entropy Formulation for Parabolic Degenerate Equations with General Dirichlet Boundary Conditions and Application to the Convergence of FV Methods.
SIAM Journal on Numerical Analysis,
Vol. 41,
Issue. 6,
p.
2262.
Küther, Marc
and
Ohlberger, Mario
2003.
Hyperbolic Problems: Theory, Numerics, Applications.
p.
675.
Makridakis, Charalambos
and
Perthame, Benoı⁁t
2003.
Optimal Rate of Convergence for Anisotropic Vanishing Viscosity Limit of a Scalar Balance Law.
SIAM Journal on Mathematical Analysis,
Vol. 34,
Issue. 6,
p.
1300.
Kröner, Dietmar
Küther, Marc
Ohlberger, Mario
and
Rohde, Christian
2003.
Trends in Nonlinear Analysis.
p.
289.
Barth, Timothy
and
Ohlberger, Mario
2004.
Encyclopedia of Computational Mechanics.
Ohlberger, Mario
2004.
Higher order finite volume methods on selfadaptive grids for convection dominated reactive transport problems in porous media.
Computing and Visualization in Science,
Vol. 7,
Issue. 1,
p.
41.
TADMOR, EITAN
RASCLE, MICHEL
and
BAGNERINI, PATRIZIA
2005.
COMPENSATED COMPACTNESS FOR 2D CONSERVATION LAWS.
Journal of Hyperbolic Differential Equations,
Vol. 02,
Issue. 03,
p.
697.
Kröner, D.
2005.
Computational Science and High Performance Computing.
Vol. 88,
Issue. ,
p.
367.
Ohlberger, Mario
and
Vovelle, Julien
2005.
Error estimate for the approximation of nonlinear conservation laws on bounded domains by the finite volume method.
Mathematics of Computation,
Vol. 75,
Issue. 253,
p.
113.
Hietel, D.
Junk, M.
Kuhnert, J.
and
Tiwari, S.
2005.
Analysis and Numerics for Conservation Laws.
p.
339.
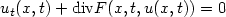 with the initial condition $u_{0}\in{L^\infty}(\mathbb{R}^N)$
with the initial condition $u_{0}\in{L^\infty}(\mathbb{R}^N)$ 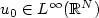 . Passing to the limit in these schemes, we prove the existence of an entropy solution $u\in{L^infty}(\mathbb{R}^N\times\mathbb{R}_+)$
. Passing to the limit in these schemes, we prove the existence of an entropy solution $u\in{L^infty}(\mathbb{R}^N\times\mathbb{R}_+)$ 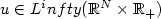 . Proving also uniqueness, we obtain the convergence of the finite volume approximation to the entropy solution in $L^p_{loc}(\mathbb{R}^N\times\mathbb{R}_+)$
. Proving also uniqueness, we obtain the convergence of the finite volume approximation to the entropy solution in $L^p_{loc}(\mathbb{R}^N\times\mathbb{R}_+)$ 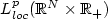 , 1 ≤ p ≤ +∞. Furthermore, if ${u_0}\in {L^\infty}\cap\mbox{BV}_{loc}(\mathbb{R}^N)$
, 1 ≤ p ≤ +∞. Furthermore, if ${u_0}\in {L^\infty}\cap\mbox{BV}_{loc}(\mathbb{R}^N)$ 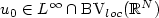 , we show that $u\in\mbox{BV}_{loc}(\mathbb{R}^N\times\mathbb{R}_+)$
, we show that $u\in\mbox{BV}_{loc}(\mathbb{R}^N\times\mathbb{R}_+)$ 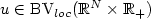 , which leads to an “ $h^{\frac{1}{4}}$
, which leads to an “ $h^{\frac{1}{4}}$ 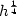 ” error estimate between the approximate and the entropy solutions (where h defines the size of the mesh).
” error estimate between the approximate and the entropy solutions (where h defines the size of the mesh).

