Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T17:55:53.383Z Has data issue: false hasContentIssue false
  • English
  • Français

Error estimates of an efficient linearization schemefor anonlinear elliptic problem with a nonlocal boundary condition

Published online by Cambridge University Press:  15 April 2002

Marian Slodička
Marian Slodička*
Affiliation:
Department of Mathematical Analysis, Faculty of Engineering, Ghent University, Galglaan 2, B-9000 Ghent, Belgium. ([email protected])
Get access

Abstract

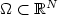We consider a nonlinear second order elliptic boundary value problem (BVP)in a bounded domain $\Omega\subset {\mathbb R}^N$ witha nonlocal boundary condition. A Dirichlet BC containing an unknown additive constant,accompanied with a nonlocal (integral) Neumann side condition is prescribed at some boundary part Γn . The rest of the boundary is equipped with Dirichlet or nonlinear Robin type BC. The solution is found via linearization. We design a robust and efficient approximation scheme. Error estimates for the linearization algorithm are derived inL 2(Ω),H 1(Ω) andL ∞(Ω) spaces.

Keywords

Nonlinear elliptic BVPerror estimatesnonstandard boundary conditionlinearization.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 35 , Issue 4 , July 2001 , pp. 691 - 711
Copyright
© EDP Sciences, SMAI, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreucci, D. and Gianni, R., Global existence and blow up in a parabolic problem with nonlocal dynamical boundary conditions. Adv. Differ. Equ. 1 (1996) 729-752.
Arnold, D.N. and Brezzi, F., Mixed and nonconforming finite element methods: implementation, postprocessing and error estimates. RAIRO Modél. Math. Anal. Numér. 19 (1985) 7-32. CrossRef
Bramble, J.H. and Lee, P., On variational formulations for the Stokes equations with nonstandard boundary conditions. RAIRO Modél. Math. Anal. Numér. 28 (1994) 903-919. CrossRef
H. Brézis, Opérateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert. North-Holland Math. Stud. 5, Notas de matemática 50, North-Holland Publishing Comp., Amsterdam, London; American Elsevier Publishing Comp. Inc., New York (1973).
H. De Schepper and M. Slodicka, Recovery of the boundary data for a linear 2nd order elliptic problem with a nonlocal boundary condition. ANZIAM J. 42E (2000) C488-C505. ISSN 1442-4436 (formerly known as J. Austral. Math. Soc., Ser. B).
L.C. Evans, Partial differential equations, Graduate Studies in Mathematics 19, American Mathematical Society (1998).
A. Friedman, Variational principles and free-boundary problems. Wiley, New York (1982).
H. Gerke, U. Hornung, Y. Kelanemer, M. Slodicka and S. Schumacher, Optimal Control of Soil Venting: Mathematical Modeling and Applications, ISNM 127, Birkhäuser, Basel (1999).
D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order. Springer, Berlin, Heidelberg (1983).
Jäger, W. and Kacur, J., Solution of doubly nonlinear and degenerate parabolic problems by relaxation schemes. RAIRO Modél. Math. Anal. Numér. 29 (1995) 605-627. CrossRef
Kacur, J., Solution to strongly nonlinear parabolic problems by a linear approximation scheme. IMA J. Numer. Anal. 19 (1999) 119-145. CrossRef
C.V. Pao, Nonlinear parabolic and elliptic equations. Plenum Press, New York (1992).
Rannacher, R. and Turek, S., Artificial boundaries and flux and pressure conditions for the incompressible Navier-Stokes equations. Internat. J. Numer. Methods Fluids 22 (1996) 325-352.
M. Slodicka, A monotone linear approximation of a nonlinear elliptic problem with a non-standard boundary condition, in Algoritmy 2000, A. Handlovicová, M. Komorníková, K. Mikula and D. Sevcovic, Eds., Bratislava (2000) 47-57.
M. Slodicka and H. De Schepper, On an inverse problem of pressure recovery arising from soil venting facilities. Appl. Math. Comput. (to appear).
M. Slodicka and H. De Schepper, A nonlinear boundary value problem containing nonstandard boundary conditions. Appl. Math. Comput. (to appear).
Slodicka, M. and Van Keer, R., A nonlinear elliptic equation with a nonlocal boundary condition solved by linearization. Internat. J. Appl. Math. 6 (2001) 1-22.
Van Keer, R., Dupré, L. and Melkebeek, J., Computational methods for the evaluation of the electromagnetic losses in electrical machinery. Arch. Comput. Methods Engrg. 5 (1999) 385-443. CrossRef