Published online by Cambridge University Press: 23 February 2006
Many inverse problems for differential equationscan be formulated as optimal control problems.It is well known that inverse problems often need tobe regularized to obtain good approximations.This work presents a systematic method to regularizeand to establish error estimates for approximations tosome control problems in high dimension, based on symplectic approximationof the Hamiltonian system for the control problem. In particularthe work derives error estimatesand constructs regularizations for numerical approximations tooptimally controlled ordinary differential equations in ${\mathbb R}^d$ 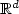 ,with non smooth control.Though optimal controls in general becomenon smooth,viscosity solutions to the corresponding Hamilton-Jacobi-Bellmanequation provide good theoretical foundation, but poor computational efficiencyin high dimensions.The computational method here uses the adjoint variable and worksefficiently also for high dimensional problems with d >> 1.Controls can be discontinuous due to a lack of regularityin the Hamiltonian or due to colliding backward paths, i.e. shocks.The error analysis, for both these cases, is based on consistency with theHamilton-Jacobi-Bellman equation, in the viscosity solution sense,and a discrete Pontryagin principle:the bi-characteristic Hamiltonian ODE system is solvedwith a C 2 approximate Hamiltonian.
The error analysis leads to estimatesuseful also in high dimensions since the bounds depend on the Lipschitznorms of the Hamiltonian and the gradient of the value functionbut not on d explicitly.Applications to inverse implied volatility estimation, in mathematical finance,and to a topology optimization problem are presented.An advantage with the Pontryagin based method is that the Newton method can be applied to efficientlysolve the discrete nonlinear Hamiltonian system,with a sparse Jacobian that can be calculated explicitly.
,with non smooth control.Though optimal controls in general becomenon smooth,viscosity solutions to the corresponding Hamilton-Jacobi-Bellmanequation provide good theoretical foundation, but poor computational efficiencyin high dimensions.The computational method here uses the adjoint variable and worksefficiently also for high dimensional problems with d >> 1.Controls can be discontinuous due to a lack of regularityin the Hamiltonian or due to colliding backward paths, i.e. shocks.The error analysis, for both these cases, is based on consistency with theHamilton-Jacobi-Bellman equation, in the viscosity solution sense,and a discrete Pontryagin principle:the bi-characteristic Hamiltonian ODE system is solvedwith a C 2 approximate Hamiltonian.
The error analysis leads to estimatesuseful also in high dimensions since the bounds depend on the Lipschitznorms of the Hamiltonian and the gradient of the value functionbut not on d explicitly.Applications to inverse implied volatility estimation, in mathematical finance,and to a topology optimization problem are presented.An advantage with the Pontryagin based method is that the Newton method can be applied to efficientlysolve the discrete nonlinear Hamiltonian system,with a sparse Jacobian that can be calculated explicitly.