Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T18:23:25.206Z Has data issue: false hasContentIssue false
  • English
  • Français

A posteriori error estimates for vertex centered finite volume approximations of convection-diffusion-reaction equations

Published online by Cambridge University Press:  15 April 2002

Mario Ohlberger
Mario Ohlberger*
Affiliation:
Institut für Angewandte Mathematik, Universität Freiburg, Hermann-Herderstr. 10, 79104 Freiburg, Germany. ([email protected])
Get access

Abstract

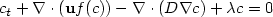This paper is devoted to the study of a posteriori error estimates for the scalar nonlinear convection-diffusion-reaction equation $c_t + \nabla \cdot ( {\bf u}f(c)) - \nabla \cdot (D \nabla c) + \lambda c = 0$ .The estimates for the error between the exact solution and an upwind finite volume approximation to the solution are derived in the L 1-norm,independent of the diffusion parameter D. The resulting a posteriori error estimate is used to define an grid adaptive solution algorithm for the finite volume scheme. Finally numerical experiments underline the applicability of the theoretical results.

Keywords

A posteriori error estimatesconvection diffusion reaction equationfinite volume schemesadaptive methodsunstructured grids.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 35 , Issue 2 , March 2001 , pp. 355 - 387
Copyright
© EDP Sciences, SMAI, 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

L. Angermann, An introduction to finite volume methods for linear elliptic equations of second order. Preprint 164, Institut für Angewandte Mathematik, Universität Erlangen (1995).
Lutz Angermann, A finite element method for the numerical solution of convection-dominated anisotropic diffusion equations. Numer. Math. 85 (2000) 175-195. CrossRef
P. Angot, V. DolejšÍ, M. Feistauer and J. Felcman, Analysis of a combined barycentric finite volume - finite element method for nonlinear convection diffusion problems. Appl. Math., Praha 43 (1998) 263-311.
Babuska, I. and Rheinboldt, W.C., Error estimators for adaptive finite element computations. SIAM J. Numer. Anal. 15 (1978) 736-754. CrossRef
Bänsch, E., Local mesh refinement in 2 and 3 dimensions. IMPACT Comput. Sci. Engrg. 3 (1991) 181-191. CrossRef
Becker, R. and Rannacher, R., A feed-back approach to error control in finite element methods: Basic analysis and examples. East-West J. Numer. Math. 4 (1996) 237-264.
Bouchut, F. and Perthame, B., Kruzkov's estimates for scalar conservation laws revisited. Trans. Amer. Math. Soc. 350 (1998) 2847-2870. CrossRef
Carrillo, J., Entropy solutions for nonlinear degenerate problems. Arch. Ration. Mech. Anal. 147 (1999) 269-361. CrossRef
Chainais-Hillairet, C., Finite volume schemes for a nonlinear hyperbolic equation. Convergence towards the entropy solution and error estimates. ESAIM: M2AN 33 (1999) 129-156. CrossRef
S. Champier, Error estimates for the approximate solution of a nonlinear hyperbolic equation with source term given by finite volume scheme. Preprint, UMR 5585, Saint-Etienne University (1998).
G. Chavent and J. Jaffre, Mathematical models and finite elements for reservoir simulation. Elsevier, New York (1986).
Cockburn, B., Coquel, F. and Lefloch, P.G., An error estimate for finite volume methods for multidimensional conservation laws. Math. Comput. 63 (1994) 77-103. CrossRef
Cockburn, B. and Gau, H., A posteriori error estimates for general numerical methods for scalar conservation laws. Comput. Appl. Math. 14 (1995) 37-47.
Cockburn, B. and Gremaud, P.A., A priori error estimates for numerical methods for scalar conservation laws. Part I: The general approach. Math. Comput. 65 (1996) 533-573. CrossRef
Cockburn, B. and Gripenberg, G., Continuous dependence on the nonlinearities of solutions of degenerate parabolic equations. J. Differential Equations 151 (1999) 231-251. CrossRef
W. Dörfler, Uniformly convergent finite-element methods for singularly perturbed convection-diffusion equations. Habilitationsschrift, Mathematische Fakultät, Freiburg (1998).
Eriksson, K. and Johnson, C., Adaptive streamline diffusion finite element methods for stationary convection-diffusion problems. Math. Comput. 60 (1993) 167-188. CrossRef
Eriksson, K. and Johnson, C., Adaptive finite element methods for parabolic problems. II: Optimal error estimates in L∞L2 and L∞L∞ . SIAM J. Numer. Anal. 32 (1995) 706-740. CrossRef
Eriksson, K. and Johnson, C., Adaptive finite element methods for parabolic problems. IV: Nonlinear Problems. SIAM J. Numer. Anal. 32 (1995) 1729-1749. CrossRef
S. Evje, K.H. Karlsen and N.H. Risebro, A continuous dependence result for nonlinear degenerate parabolic equations with spatial dependent flux function. Preprint, Department of Mathematics, Bergen University (2000).
Eymard, R., Gallou, T.ët, M. Ghilani and R. Herbin, Error estimates for the approximate solution of a nonlinear hyperbolic equation given by finite volume schemes. IMA J. Numer. Anal. 18 (1998) 563-594. CrossRef
R. Eymard, T. Gallouët, R. Herbin and A. Michel, Convergence of a finite volume scheme for nonlinear degenerate parabolic equations. Preprint LATP 00-20, CMI, Provence University, Marseille (2000).
Frolkovic, P., Maximum principle and local mass balance for numerical solutions of transport equations coupled with variable density flow. Acta Math. Univ. Comenian. 67 (1998) 137-157.
J. Fuhrmann and H. Langmach, Stability and existence of solutions of time-implicit finite volume schemes for viscous nonlinear conservation laws. Preprint 437, Weierstraß-Institut, Berlin (1998).
R. Helmig, Multiphase flow and transport processes in the subsurface: A contribution to the modeling of hydrosystems. Springer, Berlin, Heidelberg (1997).
Herbin, R., An error estimate for a finite volume scheme for a diffusion-convection problem on a triangular mesh. Numer. Methods Partial Differential Equation 11 (1995) 165-173. CrossRef
P. Houston and E. Süli, Adaptive lagrange-galerkin methods for unsteady convection-dominated diffusion problems. Report 95/24, Numerical Analysis Group, Oxford University Computing Laboratory (1995).
Jaffre, J., Décentrage et élements finis mixtes pour les équations de diffusion-convection. Calcolo 21 (1984) 171-197. CrossRef
John, V., Maubach, J.M. and Tobiska, L., Nonconforming streamline-diffusion-finite-element-methods for convection-diffusion problems. Numer. Math. 78 (1997) 165-188. CrossRef
C. Johnson, Finite element methods for convection-diffusion problems, in Proc. 5th Int. Symp. (Versailles, 1981), Computing methods in applied sciences and engineering V (1982) 311-323.
K.H. Karlsen and N.H. Risebro, On the uniqueness and stability of entropy solutions of nonlinear degenerate parabolic equations with rough coefficients. Preprint 143, Department of Mathematics, Bergen University (2000).
D. Kröner, Numerical schemes for conservation laws. Teubner, Stuttgart (1997).
Kröner, D. and Ohlberger, M., A posteriori error estimates for upwind finite volume schemes for nonlinear conservation laws in multi dimensions. Math. Comput. 69 (2000) 25-39. CrossRef
D. Kröner and M. Rokyta, A priori error estimates for upwind finite volume schemes in several space dimensions. Preprint 37, Math. Fakultät, Freiburg (1996).
Kruzkov, S.N., First order quasilinear equations in several independent variables. Math. USSR Sbornik 10 (1970) 217-243. CrossRef
N.N. Kuznetsov, Accuracy of some approximate methods for computing the weak solutions of a first-order quasi-linear equation. USSR, Comput. Math. Math. Phys. 16 (1976) 159-193.
J. Málek, J. Nečas, M. Rokyta and M. Růžička, Weak and measure-valued solutions to evolutionary PDEs, in Applied Mathematics and Mathematical Computation 13, Chapman and Hall, London, Weinheim, New York, Tokyo, Melbourne, Madras (1968).
Marion, M. and Mollard, A., An adaptive multi-level method for convection diffusion problems. ESAIM: M2AN 34 (2000) 439-458. CrossRef
Nochetto, R.H., Schmidt, A. and Verdi, C., A posteriori error estimation and adaptivity for degenerate parabolic problems. Math. Comput. 69 (2000) 1-24. CrossRef
Ohlberger, M., Convergence of a mixed finite element-finite volume method for the two phase flow in porous media. East-West J. Numer. Math. 5 (1997) 183-210.
Ohlberger, M., A posteriori error estimates for finite volume approximations to singularly perturbed nonlinear convection-diffusion equations. Numer. Math. 87 (2001) 737-761. CrossRef
Rohde, Ch., Entropy solutions for weakly coupled hyperbolic systems in several space dimensions. Z. Angew. Math. Phys. 49 (1998) 470-499. CrossRef
Rohde, Ch., Upwind finite volume schemes for weakly coupled hyperbolic systems of conservation laws in 2D. Numer. Math. 81 (1998) 85-123. CrossRef
H.-G. Roos, M. Stynes and L. Tobiska, Numerical methods for singularly perturbed differential equations. Convection-diffusion and flow problems, in Springer Ser. Comput. Math. 24, Springer-Verlag, Berlin (1996).
Tadmor, E., Local error estimates for discontinuous solutions of nonlinear hyperbolic equations. SIAM J. Numer. Anal. 28 (1991) 891-906. CrossRef
R. Verfürth, A review of a posteriori error estimation and adaptive mesh-refinement techniques, in Wiley-Teubner Ser. Adv. Numer. Math., Teubner, Stuttgart (1996).
Verfürth, R., A posteriori error estimators for convection-diffusion equations. Numer. Math. 80 (1998) 641-663.
Convergence, J.P. Vila and error estimates in finite volume schemes for general multi-dimensional scalar conservation laws. I Explicit monotone schemes. ESAIM: M2AN 28 (1994) 267-295.