We study properties of Lipschitz truncations of Sobolev functions with constant and variable exponent.As non-trivial applications we use the Lipschitz truncations to provide a simplified proof of an existence result for incompressible power-law like fluids presented in[Frehse et al., SIAM J. Math. Anal34 (2003) 1064–1083]. We also establish new existence results to a class of incompressible electro-rheological fluids.

The propagation of fractures in a solid undergoing cyclic loadingsis known as the fatigue phenomenon. In this paper, we present a time continuousmodel for fatigue, in the special situation of the debonding of thin layers,coming from a time discretized version recently proposed byJaubert and Marigo [C. R. Mecanique333 (2005) 550–556].Under very general assumptions on the surface energy density andon the applied displacement, we discuss the well-posedness of ourproblem and we give the main properties of the evolution process.


For optimal control problems with ordinarydifferential equations where the $L^\infty$ 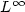-norm of the control isminimized, often bang-bang principles hold. For systems that aregoverned by a hyperbolic partial differential equation, thesituation is different:even if a weak form of the bang-bang principle still holds for the wave equation,it implies no restriction on the form of the optimal control.To illustrate thatfor the Dirichlet boundary control of the wave equation in general not even feasible controlsof bang-bang type exist,we examine the states that can be reached by bang-bang-offcontrols, that is controls that are allowed to attain only threevalues: Their maximum and minimum values and the value zero.We show that for certain control times,the difference between the initial and the terminal state can onlyattain a finite number of values.For the problems of optimal exact and approximate boundary control of the wave equationwhere the $L^\infty$ 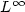-norm of the control is minimized, we introduce dual problems and present the weak form of a bang-bangprinciple, that states that the values of $L^\infty$ 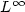-norm minimalcontrols are constrained by the sign of the dual solutions. Sincethese dual solutions are in general given as measures, thisis no restriction on the form of the control function:the dual solution may have a finite support, and when the dual solution vanishes,the control is allowed to attain all values from the intervalbetween the two extremal control values.


We prove the interior null-controllability of one-dimensionalparabolic equations with time independent measurable coefficients.

This paper presents the role of vector relative degree in theformulation of stationarity conditions of optimal control problemsfor affine control systems. After translating the dynamics into anormal form, we study the Hamiltonian structure. Stationarityconditions are rewritten with a limited number of variables. Theapproach is demonstrated on two and three inputs systems, then, weprove a formal result in the general case. A mechanical systemexample serves as illustration.

Dans ce travail, nous donnons une estimation logarithmique desdonnées de la solution u, d'un problème hyperboliqueavec condition aux limites de type Neumann, par la trace de urestreinte à un ouvert du bord, pendant un temps suffisammentgrand qui nous permet d'estimer la fonction de coût de ceproblème.

We compare a general controlled diffusion process with a deterministic systemwhere a second controller drives the disturbance against the firstcontroller. We show that the two models are equivalent withrespect to two properties: the viability (or controlledinvariance, or weak invariance) of closed smooth sets, and theexistence of a smooth control Lyapunov function ensuring thestabilizability of the system at an equilibrium.


It is shown that the Lagrange's equations for a Lagrangian system on a Lie algebroid are obtained as the equations for the critical points of the action functional defined on a Banach manifold of curves. The theory of Lagrangian reduction and the relation with the method of Lagrange multipliers are also studied.

The aim of this paper is to give a general idea to state optimality conditions of control problems in the following form: ${\displaystyle\inf_{{\displaystyle(u,v)\in {\cal U}_{ad}}}\int_{0}^{1} f\left(t, u(\theta_v(t)),u^{\prime}(t),v(t)\right){\rm d}t}$ , (1)where ${\cal U}_{ad} $ is a set of admissible controls and $\theta_v$ is the solution of the following equation: $\{ \frac{{\rm d}\theta(t)}{{\rm d}t}=g(t,\theta(t),v(t)), t\in [0,1]$ ; $\displaystyle\theta(0)=\theta_0, \theta(t)\in [0,1]\forall t$ . (2).The results are nonlocal and new.