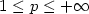Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fragalà, Ilaria
Gelli, Maria Stella
and
Pratelli, Aldo
2005.
Continuity of an optimal transport in Monge problem.
Journal de Mathématiques Pures et Appliquées,
Vol. 84,
Issue. 9,
p.
1261.
Carlier, G.
Jimenez, C.
and
Santambrogio, F.
2008.
Optimal Transportation with Traffic Congestion and Wardrop Equilibria.
SIAM Journal on Control and Optimization,
Vol. 47,
Issue. 3,
p.
1330.
Santambrogio, Filippo
2009.
Absolute continuity and summability of transport densities: simpler proofs and new estimates.
Calculus of Variations and Partial Differential Equations,
Vol. 36,
Issue. 3,
p.
343.
DUMONT, S.
and
IGBIDA, N.
2009.
On a dual formulation for the growing sandpile problem.
European Journal of Applied Mathematics,
Vol. 20,
Issue. 2,
p.
169.
Igbida, Noureddine
2009.
Equivalent formulations for Monge–Kantorovich equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 9,
p.
3805.
Champion, Thierry
and
De Pascale, Luigi
2011.
The Monge problem in Rd.
Duke Mathematical Journal,
Vol. 157,
Issue. 3,
Igbida, N.
Mazón, J.M.
Rossi, J.D.
and
Toledo, J.
2011.
A Monge–Kantorovich mass transport problem for a discrete distance.
Journal of Functional Analysis,
Vol. 260,
Issue. 12,
p.
3494.
Brasco, L.
and
Carlier, G.
2013.
Congested Traffic Equilibria and Degenerate Anisotropic PDEs.
Dynamic Games and Applications,
Vol. 3,
Issue. 4,
p.
508.
Igbida, Noureddine
2013.
Evolution Monge–Kantorovich equation.
Journal of Differential Equations,
Vol. 255,
Issue. 7,
p.
1383.
Li, Qi-Rui
Santambrogio, Filippo
and
Wang, Xu-Jia
2014.
Regularity in Monge's mass transfer problem.
Journal de Mathématiques Pures et Appliquées,
Vol. 102,
Issue. 6,
p.
1015.
Santambrogio, Filippo
2014.
Optimal Transport.
p.
22.
Santambrogio, Filippo
2015.
Optimal Transport for Applied Mathematicians.
Vol. 87,
Issue. ,
p.
249.
Benamou, Jean-David
and
Carlier, Guillaume
2015.
Augmented Lagrangian Methods for Transport Optimization, Mean Field Games and Degenerate Elliptic Equations.
Journal of Optimization Theory and Applications,
Vol. 167,
Issue. 1,
p.
1.
Santambrogio, Filippo
2015.
Optimal Transport for Applied Mathematicians.
Vol. 87,
Issue. ,
p.
219.
Azevedo, Assis
and
Santos, Lisa
2017.
Lagrange multipliers and transport densities.
Journal de Mathématiques Pures et Appliquées,
Vol. 108,
Issue. 4,
p.
592.
Dweik, Samer
and
Santambrogio, Filippo
2018.
Summability estimates on transport densities with Dirichlet regions on the boundaryviasymmetrization techniques.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 24,
Issue. 3,
p.
1167.
Igbida, Noureddine
and
Nguyen, Van Thanh
2018.
Augmented Lagrangian Method for Optimal Partial Transportation.
IMA Journal of Numerical Analysis,
Vol. 38,
Issue. 1,
p.
156.
Dweik, Samer
2018.
Lack of regularity of the transport density in the Monge problem.
Journal de Mathématiques Pures et Appliquées,
Vol. 118,
Issue. ,
p.
219.
Dweik, Samer
and
Santambrogio, Filippo
2019.
$$L^p$$
L
p
bounds for boundary-to-boundary transport densities, and
$$W^{1,p}$$
W
1
,
p
bounds for the BV least gradient problem in 2D.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 1,
Dweik, Samer
and
Górny, Wojciech
2022.
Least gradient problem on annuli.
Analysis & PDE,
Vol. 15,
Issue. 3,
p.
699.