Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T18:11:55.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Shape optimization problems for metric graphs

Published online by Cambridge University Press:  29 August 2013

Giuseppe Buttazzo ,
Berardo Ruffini  and
Bozhidar Velichkov
Giuseppe Buttazzo
Affiliation:
Dipartimento di Matematica, Università di Pisa, Largo B. Pontecorvo 5, 56127 Pisa, Italy. [email protected]
Berardo Ruffini
Affiliation:
Scuola Normale Superiore di Pisa, Piazza dei Cavalieri 7, 56126 Pisa, Italy; [email protected]; [email protected]
Bozhidar Velichkov
Affiliation:
Scuola Normale Superiore di Pisa, Piazza dei Cavalieri 7, 56126 Pisa, Italy; [email protected]; [email protected]
Get access

Abstract

We consider the shape optimization problem \hbox{$\min\big\{\E(\Gamma)\ :\ \Gamma\in\A,\ \H^1(\Gamma)=l\\big\},$}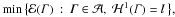min{ℰ(Γ):Γ ∈ 𝒜,ℋ1(Γ) = l}, where ℋ1 is the one-dimensional Hausdorffmeasure and𝒜is an admissible class of one-dimensional setsconnecting some prescribed set of points \hbox{$\D=\{D_1,\dots,D_k\}\subset\R^d$}𝒟 =  { D1,...,Dk }  ⊂ Rd. The cost functional ℰ(Γ) is theDirichlet energy of Γ defined through the Sobolev functions onΓ vanishing on the pointsDi. We analyze the existence of a solutionin both the families of connected sets and of metric graphs. At the end, several explicitexamples are discussed.

Keywords

Shape optimizationrectifiable setsmetric graphsquantum graphsDirichlet energy
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 20 , Issue 1 , January 2014 , pp. 1 - 22
Copyright
© EDP Sciences, SMAI, 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

L. Ambrosio, N. Fusco and D. Pallara, Functions of bounded variation and free discontinuity problems. Oxford Math. Monogr. Clarendon Press, Oxford (2000).
L. Ambrosio and P. Tilli, Topics on Analysis in Metric Spaces. Oxford Lect. Ser. Math. Appl. Oxford University Press, Oxford (2004)
Cheeger, J., Differentiability of Lipschitz functions on metric measure spaces. Geom. Funct. Anal. 9 (1999) 428–517. Google Scholar
Friedlander, L., Extremal properties of eigenvalues for a metric graph. Ann. Inst. Fourier 55 (2005) 199–211. Google Scholar
Gnutzmann, S. and Smilansky, U., Quantum graphs: Applications to quantum chaos and universal spectral statistics. Adv. Phys. 55 (2006) 527–625. Google Scholar
Kuchment, P., Quantum graphs: an introduction and a brief survey, in Analysis on graphs and its applications. AMS Proc. Symp. Pure. Math. 77 (2008) 291–312. Google Scholar
F. Maggi, Sets of Finite Perimeter and Geometric Variational Problems. Cambridge University Press, Cambridge (2012).