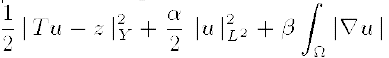We consider the problem : (P) Minimize $\lambda _{2}$ over u ∈ K ∩ X, where α≥ 0, β > 0, K is a closed convex subset of L 2(Ω), and the last additive term denotes the BV-seminorm of u, T is a linear operator from L 2 ∩ BV into the observation space Y. We formulate necessary optimality conditions for (P). Then we show that (P) admits, for givenregularization parameters α and β, solutions which depend in a stable manner on the data z. Finally we study the asymptotic behavior when α = β → 0. The regularized solutions ûβ of (P) converge to the L 2 ∩ BV minimal norm solution of the unregularized problem. The rate of convergence is β½ when the minimum-norm solution û is smooth enough.