Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brandolese, Lorenzo
2004.
Space-time decay of Navier–Stokes flows invariant under rotations.
Mathematische Annalen,
Vol. 329,
Issue. 4,
p.
685.
Brandolese, Lorenzo
2004.
Atomic decomposition for the vorticity of a viscous flow in the whole space.
Mathematische Nachrichten,
Vol. 273,
Issue. 1,
p.
28.
Brandolese, Lorenzo
2005.
Trends in Partial Differential Equations of Mathematical Physics.
Vol. 61,
Issue. ,
p.
27.
Brandolese, Lorenzo
2005.
Application of the Realization of Homogeneous Sobolev Spaces to Navier--Stokes.
SIAM Journal on Mathematical Analysis,
Vol. 37,
Issue. 2,
p.
673.
Vigneron, François
2005.
Spatial decay of the velocity field of an incompressible viscous fluid in.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 63,
Issue. 4,
p.
525.
Cannone, Marco
2005.
Vol. 3,
Issue. ,
p.
161.
Brandolese, Lorenzo
2005.
Poisson kernels and sparse wavelet expansions.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 11,
p.
3345.
Brandolese, Lorenzo
and
Vigneron, François
2007.
New asymptotic profiles of nonstationary solutions of the Navier–Stokes system.
Journal de Mathématiques Pures et Appliquées,
Vol. 88,
Issue. 1,
p.
64.
Kukavica, Igor
2009.
On the weighted decay for solutions of the Navier–Stokes system.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 6,
p.
2466.
Kukavica, Igor
and
Reis, Ednei
2011.
Asymptotic expansion for solutions of the Navier–Stokes equations with potential forces.
Journal of Differential Equations,
Vol. 250,
Issue. 1,
p.
607.
Skalák, Z.
2012.
On large‐time energy concentration in solutions to the Navier‐Stokes equations in the whole 3D space.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 92,
Issue. 10,
p.
801.
Kukavica, I.
2012.
Mathematical Aspects of Fluid Mechanics.
p.
235.
Chae, Dongho
2012.
Conditions on the Pressure for Vanishing Velocity in the Incompressible Fluid Flows in ℝN.
Communications in Partial Differential Equations,
Vol. 37,
Issue. 8,
p.
1445.
Skalák, Zdeněk
2014.
On the Characterization of the Navier–Stokes Flows with the Power-Like Energy Decay.
Journal of Mathematical Fluid Mechanics,
Vol. 16,
Issue. 3,
p.
431.
Chae, Dongho
and
Constantin, Peter
2015.
Remarks on a Liouville-Type Theorem for Beltrami Flows.
International Mathematics Research Notices,
Vol. 2015,
Issue. 20,
p.
10012.
2016.
The Navier-Stokes Problem in the 21st Century.
p.
677.
Chang, Tongkeun
and
Jin, Bum Ja
2017.
Notes on the space–time decay rate of the Stokes flows in the half space.
Journal of Differential Equations,
Vol. 263,
Issue. 1,
p.
240.
McOwen, Robert
and
Topalov, Petar
2017.
Spatial asymptotic expansions in the incompressible Euler equation.
Geometric and Functional Analysis,
Vol. 27,
Issue. 3,
p.
637.
Chang, Tongkeun
and
Jin, Bum Ja
2017.
Pointwise decay estimate of Navier–Stokes flows in the half space with slowly decreasing initial value.
Nonlinear Analysis,
Vol. 157,
Issue. ,
p.
167.
Brandolese, Lorenzo
and
Schonbek, Maria E.
2018.
Handbook of Mathematical Analysis in Mechanics of Viscous Fluids.
p.
579.
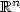 ($n\ge2$
($n\ge2$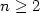 ) for arbitrarily small values of the
time variable.
We improve previous results on the spatial spreading by deducing the necessary
conditions $\int u_h(x,t)u_k(x,t)\,{\rm d}x=c(t)\delta_{h,k}$
) for arbitrarily small values of the
time variable.
We improve previous results on the spatial spreading by deducing the necessary
conditions $\int u_h(x,t)u_k(x,t)\,{\rm d}x=c(t)\delta_{h,k}$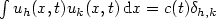 under more general assumptions on the
localization of u.
We also give some new examples of solutions which have a stronger spatial localization
than in the generic case.
under more general assumptions on the
localization of u.
We also give some new examples of solutions which have a stronger spatial localization
than in the generic case.